

03,2024年辽宁省十四地市民间大联考中考第二次模拟考试数学试题
展开注意事项 1.请在答题卡上作答,在试卷上作答无效。
2.本本试卷共23道题,满分120分。考试时间共120分钟。
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.丹东草莓开始采摘啦!每筐草莓以2.4千克为标准,超过的千克数记为正数,不足的千克数记为负数,记录-0.3 这筐草莓则实际质量是(▲ )
A.2.8千克 B.2.2 千克
C.2.1千克 D.2.4千克
2.下列图形中,既是轴对称图形又是中心对称图形的是(▲ )
3.我国的嫦娥四号探测器成功在月球背面着陆,标志着我国已经成功开始了对月球背面的研究,填补了国际空白.月球距离地球的平均距离为384000千米,数据384000用科学记数法表示为( ▲ )
A.384×10³×10⁵C.38.4×10⁴×10⁶4.下列运算正确的是(▲ )
A.−3x⁴+2x⁴=5x⁴B.x⁶÷x²=x³C.−5x⁴²=−5x⁸D.x+2²=x²+45.一元二次方程 x²−2x−4=0的根的情况是(▲ )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
6.把分式方程 22x−4=32x化为整式方程,方程两边需同时乘以(▲ )
A.2x B.2x-4 C.2x(x-2) D.2x(2x-4)
7.如图,一次函数y=kx+b的图象过点(1,-3),则当y<-3时,x的取值范围是( ▲ )
A. x>1 B. x≥1 C.x≥-3 D. x<-3
8.《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为6 210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株试卷源自 试卷上新,欢迎访问。椽的价钱,试问6 210文能买多少株椽?设6210元购买椽的数量为x株,则符合题意的方程是(▲ )
A.6210x=3x B.3(x-1)=6 210
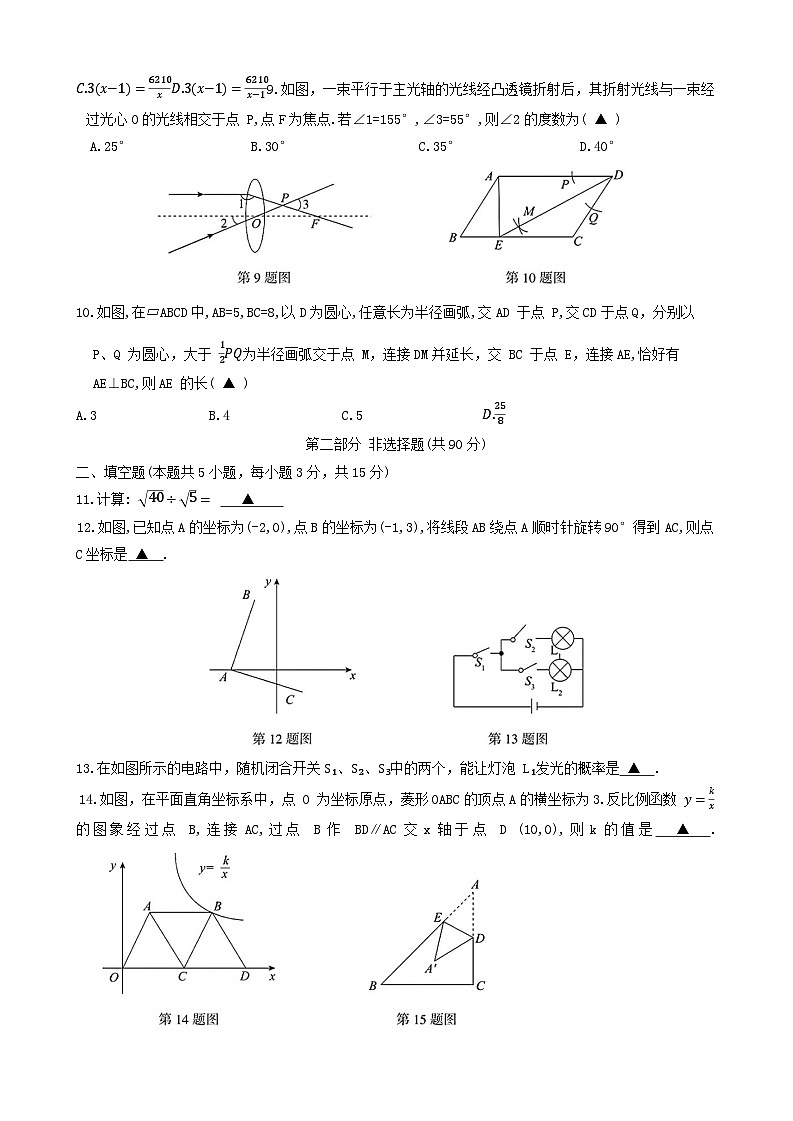
C.3x−1=6210xD.3x−1=6210x−19.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点 P,点F为焦点.若∠1=155°,∠3=55°,则∠2的度数为( ▲ )
A.25° B.30° C.35° D.40°
10.如图,在▱ABCD中,AB=5,BC=8,以D为圆心,任意长为半径画弧,交AD 于点 P,交CD于点Q,分别以 P、Q 为圆心,大于 12PQ为半径画弧交于点 M,连接DM并延长,交 BC 于点 E,连接AE,恰好有AE⊥BC,则AE 的长( ▲ )
A.3 B.4 C.5 D.258
第二部分 非选择题(共90分)
二、填空题(本题共5小题,每小题3分,共15分)
11.计算: 40÷5= ▲
12.如图,已知点A的坐标为(-2,0),点B的坐标为(-1,3),将线段AB绕点A顺时针旋转90°得到AC,则点 C坐标是 ▲ .
13.在如图所示的电路中,随机闭合开关S₁、S₂、S₃中的两个,能让灯泡 L₁发光的概率是 ▲ .
14.如图,在平面直角坐标系中,点 O 为坐标原点,菱形OABC的顶点A的横坐标为3.反比例函数 y=kx
的图象经过点 B,连接AC,过点 B作 BD∥AC交x轴于点 D (10,0),则k的值是 ▲ .
15.如图,在等腰Rt△ABC中,AC=BC=4,∠C=90°,D为边AC的中点,E为边AB上的一个动点,连接DE,将△ABC沿 DE折叠,点A 的对应点为A',当 A'E⊥AC时,BE的长度为 ▲ .
三、解答题(本题共8小题,共75分,解答应写出文字说明、演算步骤或推理过程)
16.计算(每题5分,共10分)
1−4²+−20÷−5−6×−2;2a−1a÷a2+2a+12a.17.(本小题8分)
为了节能减排,我区某校准备购买某种品牌的节能灯,已知4只A型节能灯和5 只 B型节能灯共需55元,2只A型节能灯和1只B型节能灯共需 17元.
(1)求1 只A 型节能灯和1 只 B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共300只,要求A 型节能灯的数量不超过 B型节能灯的数量的2倍,请设计出最省钱的购买方案,并说明理由.
18.(本小题9分)
某学校举办了“未成年人保护法”为主题的相关知识测试.为了了解学生对“未成年人保护法”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D 四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96.
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
八年级学生竞赛成绩扇形统计图
两组数据的平均数、中位数、众数、方差表:如
将这个扇形统计图挪上去和表格并列
根据以上信息,解答下列问题;
(1)填空:a= ▲ ,b= ▲ ,m= ▲ ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;
(3)若七年级有1000名学生参赛,八年级有900 名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
19.(本小题8分)
某品牌烤箱新增一种安全烤制模式,即在烤箱内温度匀速升至 240°C时烤箱停止加热,随后烤箱内温度下降至初始温度,如图所示的是该品牌烤箱安全烤制模式下烤箱内温度y
(℃)随时间x(分钟)变化的函数图象.
(1)求该图象的函数解析式;
(2)若食物在130℃及以上的温度中烤制6分钟以上才可健康食用,请问该模式下烤制的食物能否健康食用?请说明理由.
20.(本小题8分)
为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高AB为2cm,∠ABC=150°,支架BC为18cm,面板长DE 为24 cm,CD 为6cm.(厚度忽略不计)
(1)求支点 C离桌面l的高度;(计算结果保留根号)
(2)小吉通过查阅资料,当面板DE绕点C转动时,面板与桌面的夹角α满足 30°≤α≤70°时,能保护视力.当α从30°变化到70°的过程中,问面板上端E离桌面l的高度是增加了还是减少了?增加或减少了多少(精确到0.1cm,参考数据: sin70°≈0.94,cs70°≈0.34,tan70°≈2.75)
21.(本小题8分)
如图,AB为⊙O 直径,C,D为⊙O 上的两点,且 ∠ACD=2∠A,CE⊥DB交 DB 的延长线于点 E.
(1)求证:CE 是⊙O 的切线;
(2)若DE=2CE,AC=4,求⊙O的半径.
22.(12 分)
【问题初探】
(1)在数学活动课上,李老师给出如下问题:如图1,在等腰Rt△ABC 中, AC=BC,∠ACB=90°,点D 在AC边上,连接BD,将线段 DB 绕点 D 顺时针旋转90°得到线段DE,连接CE.求证: AD²+CD²=CE²
①如图2,小明同学从结论的角度出发给出如下解题思路:在BC 上截取 CF=AD,连接DF,将线段CE与AD,CD之间的数量关系转化为线段CE 与DF之间的数量关系.
②如图3,小亮同学从条件的角度出发,过E作EG⊥AC交AC的延长线于点 G,将线段CE 与 AD,CD之间的数量关系转化为线段CE 与 CG,EG之间的数量关系.
请你选择一名同学的解题思路,写出证明过程.
【类比分析】
(2)李老师发现之前两名同学都运用了转化思想,将要证明的线段进行转化,为了帮助学生更好地感悟转化思想,李老师将图1进行变换,并提出下面的问题,请你解答.
如图4,在等腰Rt△ABC 中, AC=BC,∠ACB=90°,点D 在AB边上,连接CD,将线段CD绕点 D 逆时针旋转90°得到线段 CE,连接DE交AC边于点 F,求证: EF²+DF²=2CF².
【类比分析】
(3)如图5,在矩形ABCD中,AB=4,AD=8,点E、F分别在边BC、DC上,∠EAF=45°,AE=2 5,连接EF,求线段 EF的长.
23.(13 分)
给定两个函数y₁,y₂,若对于任意一个x所对应的函数值y₁,y₂,我们用m(x) 表示 y₁,y₂中的较小值,即 mx=y1,y1≤y2,y2,y1>y2.则称m(x) 为关于y₁,y₂的“二元最小值函数”.
(1)已知一次函数 y₁=2x−1,y₂=−2x+3,请写出关于y₁,y₂的“二元最小值函数”m(x) ,并写出当x为何值时,函数m(x)随x的增大而增大,求函数m(x)最大值;
(2)已知二次函数 y₁=ax²−4ax+2,y₂=−ax²+4ax+2,其中a>0,求出两个函数所对应的图像的交点 A,B的坐标,并求出关于y₁,y₂的“二元最小值”m(x),写出当x为何值时,函数m(x)随x的增大而减小;
(3)直线AB与(2)中关于y₁,y₂的“二元最小值函数”m(x) 围成的封闭图形内部有四个x,y均为整数的点N(x,y),求a的取值范围;
(4)若点C为(2)中关于y₁,y₂的“二元最小值函数”m(x) 上任意一点,与A,B构成 △ABC,讨论满足 S△ABC=8a,0
平均数
中位数
众数
方差
七年级
85.2
86
b
59.66
八年级
85.2
a
91
91.76
03,2024年北京市东城区中考二模数学试题: 这是一份03,2024年北京市东城区中考二模数学试题,共28页。
03,2024年安徽省 芜湖市无为市九年级第二次联考数学试题: 这是一份03,2024年安徽省 芜湖市无为市九年级第二次联考数学试题,共5页。
20,2024年辽宁省十四地市民间大联考中考第一次模拟考试数学试题: 这是一份20,2024年辽宁省十四地市民间大联考中考第一次模拟考试数学试题,共10页。












