





人教A版 (2019)必修 第一册4.5 函数的应用(二)课文内容课件ppt
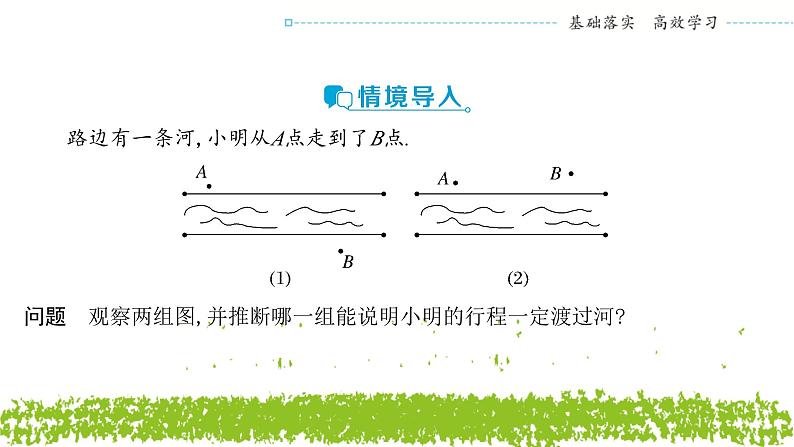
展开路边有一条河,小明从A点走到了B点.
问题 观察两组图,并推断哪一组能说明小明的行程一定渡过河?
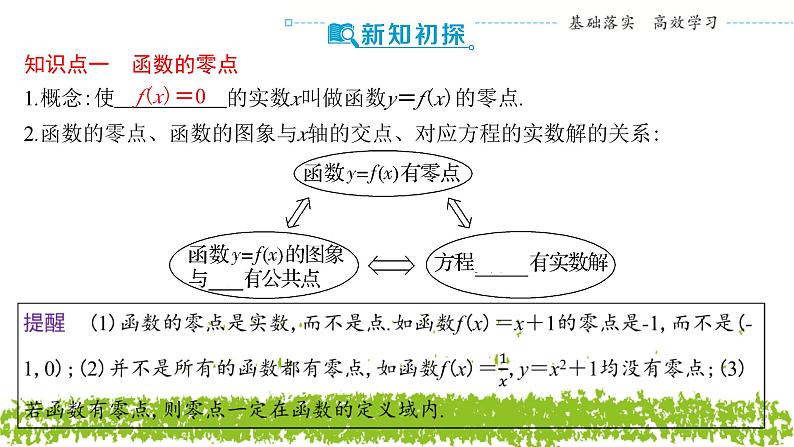
1.概念:使 f(x)=0 的实数x叫做函数y=f(x)的零点.
2.函数的零点、函数的图象与x轴的交点、对应方程的实数解的关系:
知识点二 函数零点存在定理1.条件:函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有 f(a)f(b)<0 .2.结论:函数y=f(x)在区间(a,b)内 至少有一个 零点,即 存在c∈(a,b) ,使f(c)=0,这个c也就是方程f(x)=0的解.
f(a)f(b)<0
1.函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,f(a)f(b)<0时,能否判断函数在区间(a,b)上的零点个数?
提示:只能判断有无零点,不能判断零点的个数.
2.函数y=f(x)在区间(a,b)上有零点,是不是一定有f(a)·f(b)<0?
提示:不一定,如f(x)=x2在区间(-1,1)上有零点0,但是f(-1)f(1)=1×1=1>0.
1.函数f(x)=2x2-3x+1的零点是( )
2.函数f(x)=x3-3x-3有零点的区间是( )
解析:D 因为f(2)=8-6-3=-1<0,f(3)=27-9-3=15>0,所以f(2)f(3)<0,所以D正确.
3.已知函数f(x)=-2x+m的零点为4,则实数m的值为 .
解析:f(x)=-2x+m的零点为4,所以-2×4+m=0,m=8.
(2)已知函数f(x)=ax-b(a≠0)的零点为3,求函数g(x)=bx2+ax的零点.
通性通法函数零点的求法(1)代数法:求方程f(x)=0的实数根;(2)几何法:对于不能用求根公式的方程f(x)=0,可以将它与函数y=f(x)的图象联系起来.图象与x轴的交点的横坐标即为函数的零点.
解析:C 当x≤0时,f(x)=x+1=0⇒x=-1;当x>0时,f(x)=lg2x=0⇒x=1,所以函数f(x)的所有零点构成的集合为{-1,1}.
【例2】 f(x)=ex+x-2的零点所在的区间是( )
解析 法一:∵f(0)=-1<0,f(1)=e-1>0,∴f(x)在(0,1)内有零点.
法二:ex+x-2=0,即ex=2-x,∴原函数的零点所在区间即为函数y=ex和y=2-x的图象交点的横坐标所在的区间.如图,由图象可得函数y=ex和y=2-x的图象交点所在的区间为(0,1).
通性通法确定函数f(x)零点所在区间的常用方法(1)解方程法:当对应方程f(x)=0易解时,可先解方程,再看求得的根是否落在给定区间上;(2)利用函数零点存在定理:首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点;(3)数形结合法:通过函数图象与x轴在给定区间上是否有交点来判断.
2.已知函数f(x)=2ax-a+3,若∃x0∈(-1,1),f(x0)=0,则实数a的取值范围是( )
解析:A 当a=0时,f(x)=3,不合题意,当a≠0时,由题意知f(-1)·f(1)<0,即(-3a+3)(a+3)<0,解得a<-3或a>1,故选A.
角度一:判断函数零点个数
解析 当x≤0时,令f(x)=0,即x2+2x-3=0,解得x1=-3,x2=1(舍去).当x>0时,令f(x)=0,即x-2+ln x=0,即ln x=-x+2.在同一直角坐标系中作出两函数y=ln x与y=-x+2(x>0)的图象,如图,由图可知两图象只有一个交点.综上可知,函数f(x)的零点个数为2.
通性通法判断函数零点个数的4种常用方法(1)利用方程根,转化为解方程,有几个不同的实数根就有几个零点;(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数;(3)结合单调性,利用函数零点存在定理,可判定y=f(x)在(a,b)上零点的个数;(4)转化成两个函数图象的交点问题.
通性通法 已知函数有零点(方根有根)求参数值常用的方法(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后观察求解.
解析:C 方程x+2=0(x<0)的根为x=-2,方程x2-1=0(x>0)的根为x=1,所以函数f(x)有2个零点:-2与1.
2.若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围为 .
解析:由f(x)=|2x-2|-b=0,得|2x-2|=b.在同一平面直角坐标系中分别画出y=|2x-2|与y=b的图象,如图所示.则当0<b<2时,两函数图象有两个交点,从而函数f(x)=|2x-2|-b有两个零点.
一个关系:函数零点与方程解的关系.一个定理:零点存在定理.
三种题型:求函数的零点;判断零点个数;求零点所在区间.
三种思想:特殊到一般思想;函数方程思想;数形结合思想.
1.函数f(x)=x2-8x+16的零点是( )
解析:C 由f(x)=x2-8x+16=0,得x=4,所以函数f(x)=x2-8x+16的零点是4,故选C.
2.已知定义在R上的函数f(x)的图象是连续不断的,且有如下对应值表:
那么函数f(x)一定存在零点的区间是( )
解析:C 由表可知f(1)f(2)>0,f(2)f(3)<0,f(3)f(4)>0,由函数零点存在定理可知f(x)一定存在零点的区间是(2,3).故选C.
数学必修 第一册第四章 指数函数与对数函数4.5 函数的应用(二)4.5.1 函数的零点与方程的解评课课件ppt: 这是一份数学必修 第一册<a href="/sx/tb_c4053123_t3/?tag_id=26" target="_blank">第四章 指数函数与对数函数4.5 函数的应用(二)4.5.1 函数的零点与方程的解评课课件ppt</a>,共38页。PPT课件主要包含了自主预习·新知导学,合作探究·释疑解惑,易错辨析,随堂练习,答案B,答案C等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)评课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000277_t3/?tag_id=26" target="_blank">4.5 函数的应用(二)评课课件ppt</a>,共35页。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.5 函数的应用(二)背景图课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.5 函数的应用(二)背景图课件ppt,共22页。PPT课件主要包含了题型一求函数的零点,题型三判断零点个数等内容,欢迎下载使用。













