北师大版七年级上册1.3 截一个几何体授课课件ppt

这是一份北师大版七年级上册1.3 截一个几何体授课课件ppt，共25页。PPT课件主要包含了学习导航，学习目标，新课导入，观察下面图片并思考，切水果，切黄瓜，切蛋糕，一截面，概念剖析，截面1等内容，欢迎下载使用。
1.会识别常见几何体的截面；（重点、难点）
2.经历用平面截几何体的过程，在面与体的转换中发展空间观念.
思考：如果去“切”一个几何体，会有怎样的情况？
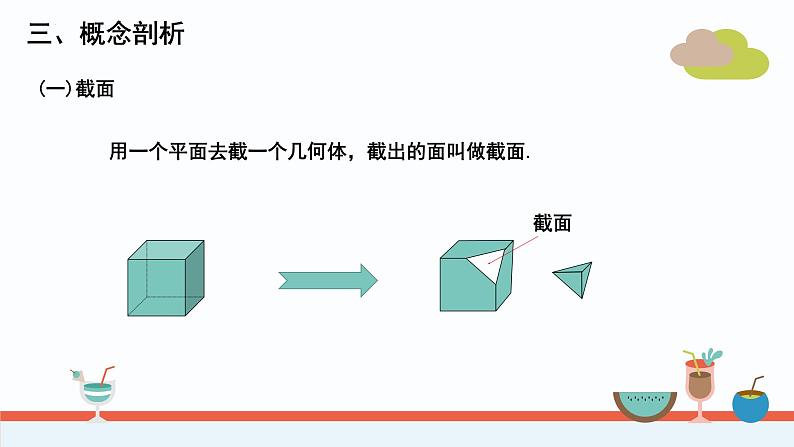
用一个平面去截一个几何体，截出的面叫做截面.
(二)正方体的截面
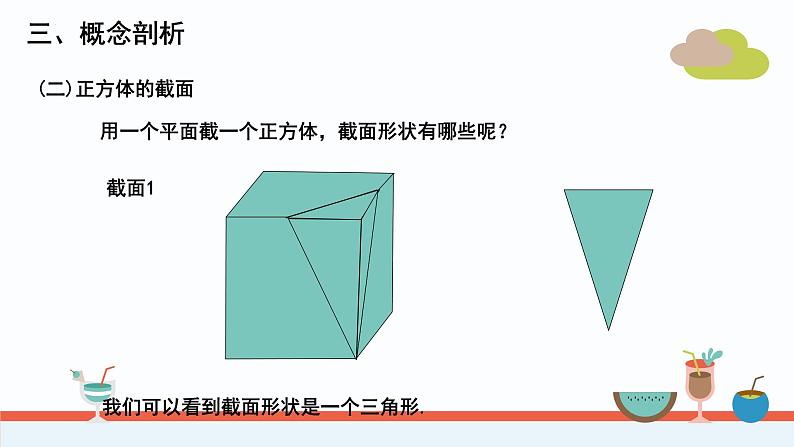
用一个平面截一个正方体，截面形状有哪些呢？
我们可以看到截面形状是一个三角形.
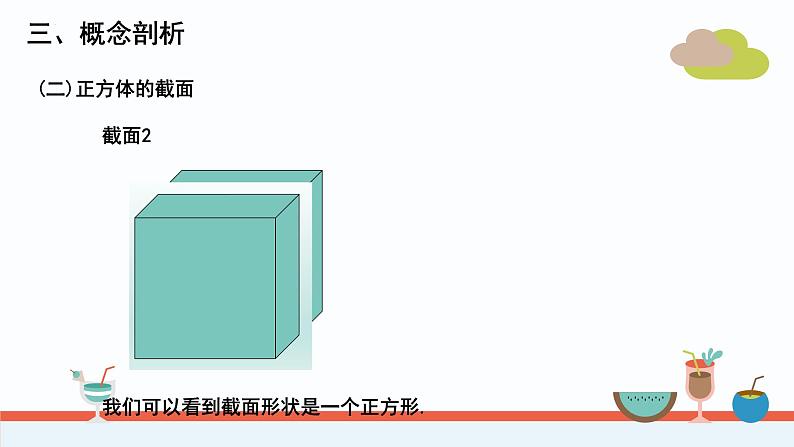
我们可以看到截面形状是一个正方形.
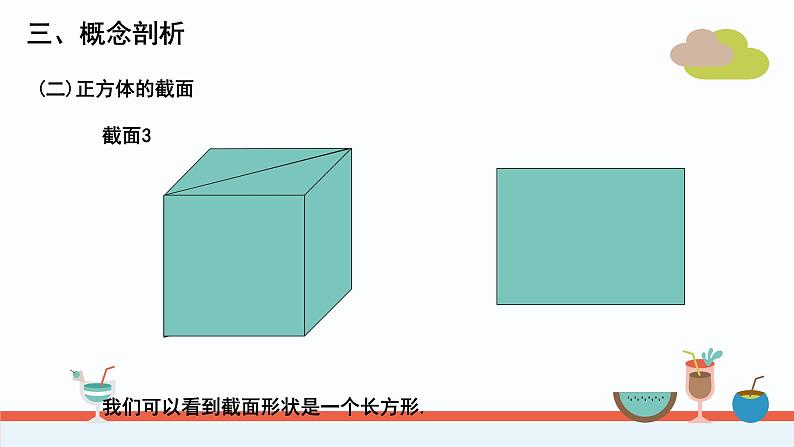
我们可以看到截面形状是一个长方形.
我们可以看到截面形状是一个梯形.
我们可以看到截面形状是一个五边形.
我们可以看到截面形状是一个六边形.
结论：正方体的截面的形状可能是三角形、四边形、五边形、六边形； 因为正方体只有6个面，所以正方体的截面的形状不可能是七边 形以上的多边形.
(三)几何体的截面
（1）平行于两底的平面截圆柱，所得截面是一个圆；
（2）垂直于底面的平面截圆柱，所得截面是一个长方形；
（3）不平行于两底的平面截圆柱，所得截面可能是一个椭圆或椭圆的 一部分或梯形.
（1）平行于底面的平面截圆锥，所得截面是一个圆；
（2）过顶点垂直于底面的平面截圆锥，所得截面是一个三角形；
（3）圆锥的截面还可能是椭圆（或椭圆的一部分）.
用平面截棱柱，得到的图形是多边形.
用平面截球体，得到的图形是只有圆.
例1．将一个正方体截去一角变成一个如图的新几何体，这个新几何体有 个面， 条棱， 个顶点．
(一)正方体的截面
分析：新几何体与原长方体比较，增加一个面，棱的条数没有变化， 顶点减少一个.
例2．如下列图形中：①等腰三角形；②矩形；③正五边形；④六边 形，只有三个是可以通过切正方体（如图）而得到的切口平面 图形，这三个图形的序号是 ．
分析：正方体利用斜截面可以截得等腰三角形和正六边形，当截面与经过相对棱的面成45°时就可得到．当截面与棱平行时，得到的切口就是矩形．
1.如图是棱长为2cm的正方体，过相邻三条棱的中点截取一个小正方体， 则剩下部分的表面积为 cm2．
分析：由于是在正方体的顶点上截取一个小正方体，去掉小正方形的三个 面的面积，同时又多出小正方形的三个面的面积，表面积没变.
2.如图所示为一个正方体截去一个角后的立体图形，如果照这样截取正方体的八个角，则新的几何体的棱有多少条？请说明你的理由
解：由一个正方体有12条棱，截取一个角多出3条棱， 即截取8个角共3×8条棱； ∴12+3×8=36条， 故新的几何体的棱有36条.
例3.用一个平面去截一个几何体，如果截面的形状是圆，则该几何体可能是（ ） A．正方体 B．三棱柱 C．四棱锥 D．球
(二)几何体的截面
分析：根据正方体、三棱柱、四棱柱和球的特点判断即可;正方体、三棱柱、四棱柱的截面不可能为圆，而球的截面为圆.故选D.
例4.请问：平面图形①②③④⑤分别可由平面截几何体A、B、C、D中的 哪些得到？
分析：根据正方体、三棱锥、圆锥、圆柱的形状判断即可，可用排除法.
解：由根据图形可得出： 平面图形①可由平面截几何体A、B、D得到； 图形②可截几何体B得到；图形③可截几何体B、C得到； 图形④可截几何体B、C、D得到；图形⑤可截几何体A、C得到.
3.如图是一个三棱柱，用平面从中截去一个三棱柱后，剩下的几何体是 .（写出所有可能的结果）
分析：此题是截去一个三棱柱，切法很关键，我们可以选择最简单、最直观的做法，从三棱柱正中切下一刀，那么切下一个三棱柱，还剩一个三棱柱．从三棱柱竖直方向切下一刀，那么切下一个三棱柱，还剩一个四棱柱.
4.如用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②三棱锥；③圆柱；④圆锥 .（写出所有正确结果的序号）
分析：当截面的角度和方向不同时，圆柱体的截面无论什么方向截取圆柱 都不会截得三角形.