宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学（文）试卷(含答案)

这是一份宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学（文）试卷(含答案)，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知集合,则与集合A的关系为( )
A.B.C.,D.
2．已知复数z满足,其中i为虚数单位,则复数z的虚部是( )
A.B.-1C.1D.
3．已知平面向量,,且,则( )
A.2B.C.D.-2
4．命题“,”的否定是( )
A.,B.,
C.,D.,
5．下列函数中既是奇函数又在区间上单调递增的是( )
A.B.C.D.
6．如下图,在边长为a的正方形内有不规则图形,向正方形内随机撒豆子,若撒在图形内和正方形内的豆子数分别为m,n,则图形面积的估计值为( )
A.B.C.D.
7．某班有学生50人,现将所有学生按1,2,3,…,50随机编号,若采用系统抽样的方法抽取一个容量为5的样本(等距抽样),已知编号为4,a,24,b,44号学生在样本中,则( )
A.48B.34C.14D.8
8．已知曲线在点处的切线方程为，则( )
A.，B.，
C.，D.，
9．已知m,n为两条直线,,为两个平面,,,则是的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
10．已知数列满足,,,设其前n项和为,则( )
A.2500B.2600C.2700D.2800
11．将函数的图象上所有点的横坐标缩短到原来的,纵坐标不变,得到函数的图象．若在上有且仅有3个极值点,则的取值范围为( )
A.B.C.D.
12．定义在R上的偶函数满足,且当 时,,若关于x的方程恰有5个实数解,则实数m的取值范围为( )
A.B.C.D.
二、填空题
13．设x,y满足约束条件,则的最大值为______.
14．在各项均为正数的等比数列中,,则__________.
15．已知双曲线的左右焦点分别为、,曲线C上的点M满足,,,则双曲线的离心率为__________．
16．已知正四棱锥的底面边长为2,高为4,它的所有顶点都在同一球面上,则这个球的表面积是__________.
三、解答题
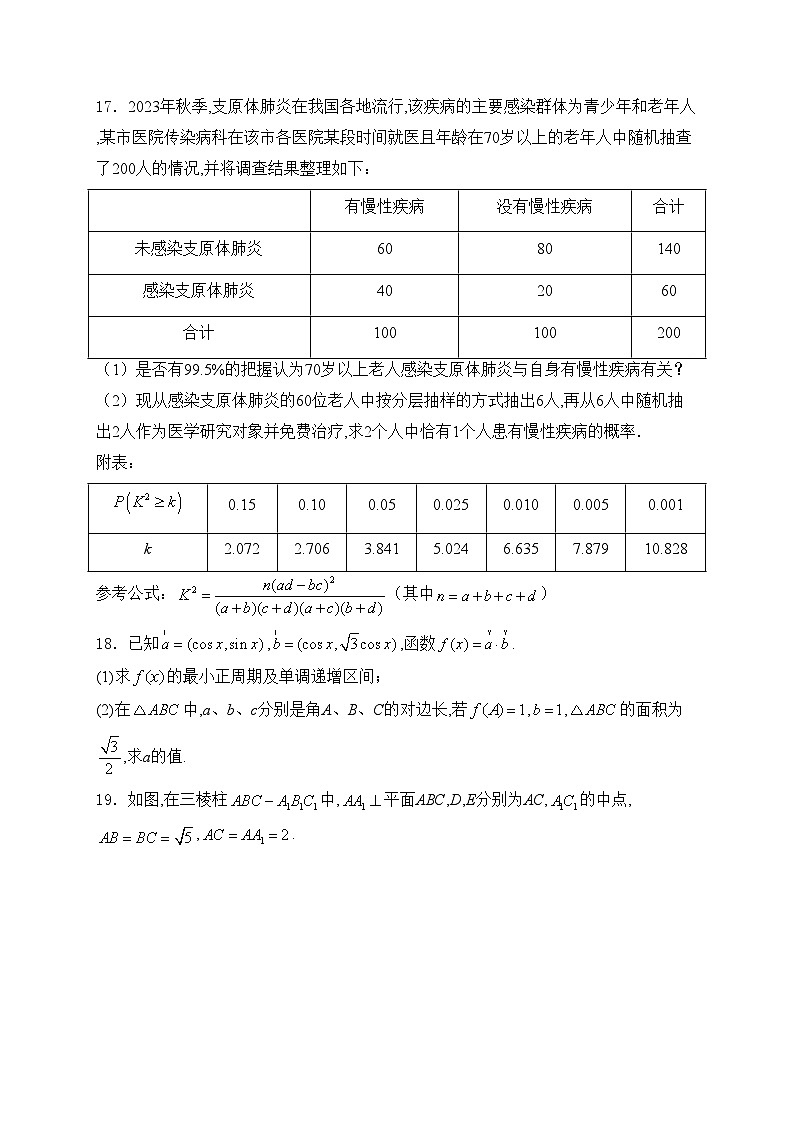
17．2023年秋季,支原体肺炎在我国各地流行,该疾病的主要感染群体为青少年和老年人,某市医院传染病科在该市各医院某段时间就医且年龄在70岁以上的老年人中随机抽查了200人的情况,并将调查结果整理如下：
（1）是否有99.5%的把握认为70岁以上老人感染支原体肺炎与自身有慢性疾病有关？
（2）现从感染支原体肺炎的60位老人中按分层抽样的方式抽出6人,再从6人中随机抽出2人作为医学研究对象并免费治疗,求2个人中恰有1个人患有慢性疾病的概率．
附表：
参考公式：（其中）
18．已知,,函数.
(1)求的最小正周期及单调递增区间；
(2)在中,a、b、c分别是角A、B、C的对边长,若,,的面积为,求a的值.
19．如图,在三棱柱中,平面ABC,D,E分别为AC,的中点,,.
(1)求证：平面；
(2)求点D到平面ABE的距离.
20．已知椭圆的半焦距为,且过点.
（1）求椭圆的方程;
（2）设直线交椭圆C于A,B两点,且线段的中点M在直线上,求证：线段的中垂线恒过定点N.
21．设函数.
（1）若，求函数的单调区间；
（2）设函数在上有两个零点，求实数a的取值范围.（其中e是自然对数的底数）
22．以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.在平面直角坐标系中,已知直线l过点,且倾斜角为.
(1)求曲线C的直角坐标方程和直线l的参数方程；
(2)设点M的直角坐标为,直线l与曲线C的交点为A,B,求的值.
23．已知.
(1)当时,求不等式的解集；
(2)若,恒成立,求实数m的取值范围.
参考答案
1．答案：B
解析：
故选：B.
2．答案：B
解析：由复数,可得,
所以复数z的虚部是-1．
故选：B．
3．答案：D
解析：因为,,且,所以,
解得,所以D正确.
故选：D.
4．答案：D
解析：命题“,”,
命题否定为：,.
故选：D.
5．答案：B
解析：对于A,为偶函数,不符合题意;
对于B,为奇函数,且在区间上单调递增,符合题意;
对于C,为奇函数,在上单调递减,在上单调递增,不符合题意;
对于D,为奇函数,,当时,,函数在上单调递减,不符合题意．
故选：B．
6．答案：C
解析：由题意知在正方形中随机投掷n个点,则n个点中有m个点落入中,
不规则图形的面积：正方形的面积,
不规则图形面积正方形的面积．
故选：C．
7．答案：A
解析：因为,所以组距为10,
因为第一个被抽取的编号为4,所以,,
所以.
故选：A.
8．答案：C
解析：，，
，．将代入得，．
故选：C．
9．答案：A
解析：若,因为,所以,即由可以得到,
若,如图,在正方体中,取平面为平面,平面为平面,
取为直线m,为直线n,显然有,,,,但m与不垂直,即由得不到,
故选：A.
10．答案：B
解析：若,,则,
若,,则,
所以数列的偶数项构成以2为首项,公差为2的等差数列,奇数项构成常数数列,
.
故选：B.
11．答案：C
解析：由题可知,,当时,．
因为在上有且仅有3个极值点,所以,解得,
所以的取值范围为：．
故选：C.
12．答案：A
解析：因为,所以的图象关于直线对称,
又是定义在R上的偶函数,所以的图象关于直线对称,
作出函数与函数的图象如图所示,
若关于x的方程恰有5个实数解,
则函数与函数的图象有5个交点,
所以,解得.
故选：A.
13．答案：4
解析：作出可行域如下：
由可得,由图可知当直线过点时,
最小,则z最大,此时.
故答案为：4.
14．答案：3
解析：.
故答案为：3.
15．答案：
解析：因为,,所以,
又,所以,,
所以,
则,即双曲线的离心率为.
故答案为：.
16．答案：
解析：如图,正四棱锥的外接球的球心O在它的高上,记外接球半径为R,
,,,底面正方形边长为2,
在中,,可得,解得,
球的表面积
故答案为：.
17．答案：（1）有的把握认为70岁以上老人感染支原体肺炎与自身有慢性疾病有关;
（2）
解析：（1）根据题意得：.
有的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关.
（2）从感染支原体肺炎的60位老人中按分层抽样的方式抽出6人,其中有慢性疾病有人,
没有慢性疾病有2人,
设有慢性疾病的4人编号为a,b,c,d,没有慢性疾病的2人编号为e,f,
从中任取2人有：,,,,,,,,,,,,,共15种情况,
2个人中恰有1个人患有慢性疾病的有,,,,,,,共8种情况,
由古典概型的概率公式可得：2个人中恰有1个人患有慢性疾病的概率为.
18．答案：(1),递增区间为,
(2).
解析：(1)
即.故最小正周期为.
单调递增区间：,.
故,递增区间为,.
(2)由得,因为.
故,故.
又,故.
故,故.
19．答案：（1）答案见解析
（2）
解析：（1）证明： ,D,E分别为AC,的中点,
,且,又平面,∴平面,
又平面, ,
又,且,,平面,
平面.
（2）,,, ,
,,.
在中,,,边上的高为.
.设点D到平面ABE的距离为d,
根据,得,解得,
所以点D到平面ABE的距离为.
20．答案：（1）
（2）证明见解析
解析：（1）椭圆过点,即,又,
又,则,
即椭圆方程为.
（2）由得,
,设,,则,
设的中点M为,
得,即,得,
所以.
所以的中垂线方程为,即,
故中垂线恒过点.
21．答案：（1）的单调递增区间为，单调递减区间为
（2）
解析：（1）当时，，的定义域为，
，
令，则，解得，
令，则，解得.
函数的单调递增区间为，单调递减区间为.
（2）令，则.
令，其中，
则.
令，解得，令，解得.
的单调递减区间为，单调递增区间为，
.
又，，函数在上有两个零点，
的取值范围是.
22．答案：(1),(t为参数)
(2)
解析：(1)把,展开得,
两边同乘得①.
将,,代入①,
即得曲线C的直角坐标方程为,
又直线l过点,且倾斜角为,则l的参数方程为(t为参数).
(2)将代入,得,
点M的直角坐标为,设这个方程的两个实数根分别为,,
则,,,
则由参数t的几何意义即得.
23．答案：(1)
(2)或
解析：(1)当时,等价于
或或,
所以,或,或,
综上可得：,
不等式的解集为.
(2)恒成立,恒成立,
(当且仅当时等号成立),
,解得,,
m的取值范围是或.
有慢性疾病
没有慢性疾病
合计
未感染支原体肺炎
60
80
140
感染支原体肺炎
40
20
60
合计
100
100
200
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828