

所属成套资源:2024年中考数学【高分·突破】考点特训卷练习(原卷版+解析)
2024年中考数学【高分·突破】考点06二次函数的解析式、图像及其性质(原卷版+解析)
展开
这是一份2024年中考数学【高分·突破】考点06二次函数的解析式、图像及其性质(原卷版+解析),共34页。
一、单选题
1.如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和,其图像与x轴围成封闭图形L,图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( )
A.B.C.D.
2.如图1,在中,,的长为a,动点D在边上从点A向点B运动,过点D作,垂足分别为E,F,设的长为x,矩形的面积为y,y随x变化的关系图象如图2所示,其中点P为图象的最高点,且纵坐标为,则a的值为( )
A.2B.4C.6D.8
3.雁门关,位于我省忻州市雁门山中,是长城上的重要关隘,以“险”著称,被誉为“中华第一关”,由于地理环境特殊,行车高速路上的隧道较多,如图①是雁门关隧道,其截面为抛物线型,如图②为截面示意图,线段表示水平的路面,以O为坐标原点,所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A.B.
C.D.
4.已知二次函数(a为常数)经过点,图象与x轴交于点A、B(A在B的左边),连接,点P是抛物线图象在第一象限内的一点,过点P作交于点Q,若取得最大值,则此时点P的横坐标为( )
A.B.C.1D.2
5.如图,已知在抛物线上有一点,轴于B点,连接,将绕O点顺时针方向旋转一定的角度后,该三角形的A.B两点中必有一个顶点落在抛物线上,这个角度是( )
A.B.C.D.
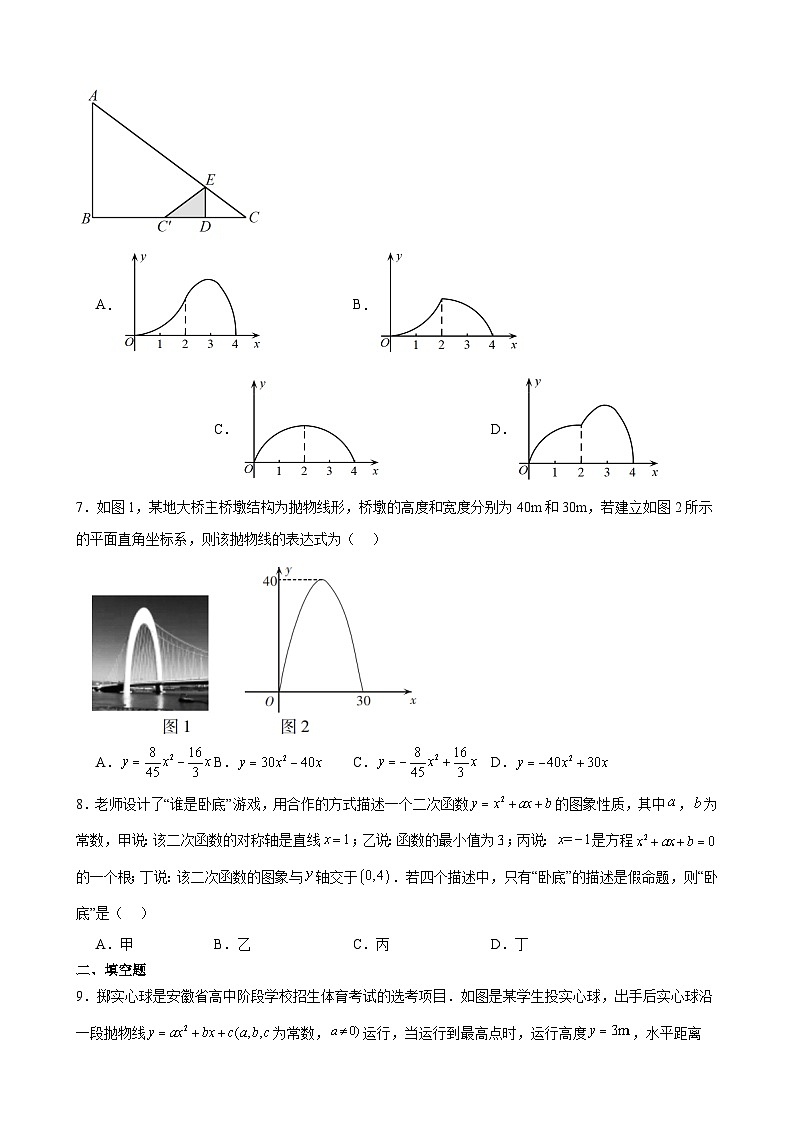
6.如图,在中,,,点从点出发沿方问以向点匀速运动,过点作于点.以所在直线为对称轴,将折叠,点的对应点为,移动过程中与重叠部分的面积为,运动时间为,则与之间函数关系的图象大致是( )
A. B. C. D.
7.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A.B.C.D.
8.老师设计了“谁是卧底”游戏,用合作的方式描述一个二次函数的图象性质,其中,为常数,甲说:该二次函数的对称轴是直线;乙说:函数的最小值为;丙说:是方程的一个根;丁说:该二次函数的图象与轴交于.若四个描述中,只有“卧底”的描述是假命题,则“卧底”是( )
A.甲B.乙C.丙D.丁
二、填空题
9.掷实心球是安徽省高中阶段学校招生体育考试的选考项目.如图是某学生投实心球,出手后实心球沿一段抛物线为常数,运行,当运行到最高点时,运行高度,水平距离.
(1)当出手高度为时, ;
(2)若实心球落地水平距离不小于,且不超过,则的取值范围是 .
10.已知拋物线与直线相交于点(点在点右侧),且.
(1)的值是 .
(2)直线与抛物线相交于点,与直线相交于点,.若随的增大而增大,则的取值范围是 .
11.如图①,是可移动的灌溉装置,以水平地面方向为x轴,点O为原点建立直角坐标系,点A在y轴上,如图②所示.其水柱的高度y(单位:m)与水柱距喷水头的水平距离x(单位:m)近似满足函数关系式.在图②中,若水柱在某一个高度时总对应两个不同的水平位置,则x的取值范围是 .
12.在平面直角坐标系中,对封闭图形和不重合的两点,给出如下定义:点关于点的中心对称点为,若点在图形内(包含边界),则称图形为点经点投射的“靶区”.如图,拋物线与轴的交点A,位于原点两侧(点A在点的左侧),且,则抛物线的函数表达式为 ,记轴上方的拋物线与轴所围成的封闭图形为,点为轴上一动点,若直线上存在点,使得图形为点经点投射的“靶区”,则的取值范围是 .
13.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
14.某游乐园要建造一个直径为的圆形喷水池,计划在喷水池的周边安装一圈喷水头,使喷出的水柱距池中心处达到最高,高度为.以水平方向为轴,喷水池中心为原点建立直角坐标系如图,若要在喷水池中心的正上方设计挡板(),使各方向喷出的水柱擦挡板后,汇合于喷水池中心装饰物M处,挡板所在直线的表达式为,则抛物线l的表达式为 ,n的值为
15.如图,抛物线与y轴交于点A,过的中点作轴,交抛物线于B、C两点(点B在C的左边),连接、,若将向上平移使得B、C两点恰好落在抛物线上,则点O平移后的坐标为 .
16.如图,在平面直角坐标系中,二次函数的图象与坐标轴相交于A,B,C三点,连接,.已知点E坐标为,点D在线段上,且.则四边形面积的大小为 .
三、解答题
17.已知抛物线与x轴负半轴交于点A,与y轴交于点B.现将抛物线平移,使平移后的抛物线过点B和点.
(1)求抛物线的表达式;
(2)点为抛物线上一点,过点P作y轴平行线,交直线于点M,过点P作x轴平行线,交y轴于点N,当与相似时,求点P坐标.
18.湘雅公园人工湖上有一座拱桥,横截面呈抛物线形状,如图所示,现对此展开研究:跨度为4米,桥墩露出水面的高度为米,在距点A水平距离为2米的地点,拱桥距离水面的高度为米,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是横截水面,是拱桥距水面的高度.
(1)求抛物线的表达式;
(2)公园欲开设游船项目,为安全起见,公园要在水面上的C、D两处设置航行警戒线,并且,要求游船能从C、D两点之间安全通过,则C处距桥墩的距离CE至少为多少米?
19.在平面直角坐标系中,二次函数的图象如图所示,该抛物线的顶点为,且与轴的交点为,连接过点作轴的平行线与抛物线交于另一点,过点作的垂线.
(1)当时,求的长;
(2)如图,延长交于点,请用含的代数式表示的面积;
(3)如图,点在抛物线第一象限的图象上且位于点的左侧,连接并延长交于点,过点作垂直于,垂足为点,连接求证:.
20.综合实践
(1)填空:在上图中位似中心是点________;________多边形是特殊的________多边形.(填“位似”或“相似”)
(2)在平面直角坐标系中(如下图),二次函数的图像与x轴交于点A,点B是此函数图像上一点(点A、B均不与点O重合),已知点B的横坐标与纵坐标相等,以点O为位似中心,相似比为,将缩小,得到它的位似.
①画出,并求经过O、、三点的抛物线的表达式;
②直线与二次函数的图像交于点M,与①中的抛物线交于点N,请判断和是否为位似三角形,并根据新定义说明理由.
九年级第一学期教材第2页
结合教材图形给出新定义
对于下图中的三个四边形,通常可以说,缩小四边形,得到四边形;放大四边形,得到四边形.
图形的放大或缩小,称为图形的放缩运动.将一个图形放大或缩小后,就得到与它形状相同的图形.图中,四边形和四边形都与四边形形状相同.我们把形状相同的两个图形说成是相似的图形,或者就说是相似形.
如图,对于两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形,这个点就是位似中心.
压轴热点考点06 二次函数的解析式、图像及其性质
压轴突破——2024年【中考·冲刺】数学高频热点考点好题精编
一、单选题
1.如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和,其图像与x轴围成封闭图形L,图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( )
A.B.C.D.
【答案】B
【分析】依照题意画出图形,结合图形找出关于a的不等式组,解之即可得出结论.
【详解】解:∵二次函数的图象与x轴的交点为A、D的横坐标分别为3和,
∴二次函数解析式为,对称轴为直线,
当时,,,
∴抛物线顶点坐标为,与y轴的交点坐标为,
如图所示,∵图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),
∴,
解得,
∴四个选项中只有B选项符合题意,
故选B.
【点睛】考查了二次函数图象的性质,抛物线与x轴的交点坐标,解题时,利用了数形结合的数学思想,难度较大.
2.如图1,在中,,的长为a,动点D在边上从点A向点B运动,过点D作,垂足分别为E,F,设的长为x,矩形的面积为y,y随x变化的关系图象如图2所示,其中点P为图象的最高点,且纵坐标为,则a的值为( )
A.2B.4C.6D.8
【答案】B
【分析】本题考查二次函数的实际应用,根据含30度角的直角三角形的性质,得到,,勾股定理,得到,求出的长,利用矩形的面积公式得到二次函数关系式,利用二次函数的性质进行求解即可.
【详解】解:∵,的长为x,的长为a,
∴在中,,在中,,
∴,,
∴,
∴,
由图象可知:,
∴(负值已舍去).
故选:B.
3.雁门关,位于我省忻州市雁门山中,是长城上的重要关隘,以“险”著称,被誉为“中华第一关”,由于地理环境特殊,行车高速路上的隧道较多,如图①是雁门关隧道,其截面为抛物线型,如图②为截面示意图,线段表示水平的路面,以O为坐标原点,所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A.B.
C.D.
【答案】D
【分析】根据题意得出,,设抛物线的表达式为,把代入得,再把代入求出a的值,即可得出抛物线表达式.
【详解】解:∵,抛物线的顶点P到的距离为,
∴,,
设抛物线的表达式为,
把代入得:,
把代入得:,
解得:,
∴抛物线表达式为,
故选:D.
【点睛】本题主要考查了求抛物线的表达式,解题的关键是掌握用待定系数法求函数表达式的方法和步骤,以及二次函数的顶点式.
4.已知二次函数(a为常数)经过点,图象与x轴交于点A、B(A在B的左边),连接,点P是抛物线图象在第一象限内的一点,过点P作交于点Q,若取得最大值,则此时点P的横坐标为( )
A.B.C.1D.2
【答案】D
【分析】作于点H,交于D,可推证,说明的函数值一定,最大时,满足最大;待定系数法确定直线解析式,设点P坐标,表示出,运用二次函数最值,确定点坐标即可.
【详解】解:∵图象经过点,
∴,
∴,
将a代入关系式得,,
令,即,
解得,,,
∴,,
∴,,,
设解析式,得
,解得
∴,
作于点H,交于D,则
∴
∴,
∴,
∴最大时,满足最大,
设点,则点,
∴
∴当时,有最大值.
故选:D.
【点睛】本题考查了二次函数的性质的应用,锐角三角函数,平行线的性质,待定系数法确定函数解析式,由三角函数确定线段间的数量关系是解题关键.
5.如图,已知在抛物线上有一点,轴于B点,连接,将绕O点顺时针方向旋转一定的角度后,该三角形的A.B两点中必有一个顶点落在抛物线上,这个角度是( )
A.B.C.D.
【答案】B
【分析】如图,设抛物线与y轴的交点为点C,则点C坐标为,再根据可得当点A与抛物线顶点C重合时满足题意,再利用锐角三角函数求得,从而求得旋转角度.
【详解】解:如图,设抛物线与y轴的交点为点C,则点C坐标为,
∵,轴于B点,
∴,,,
∵,
∴,
∴,
∴将绕O点顺时针方向旋转,该三角形的A与抛物线的顶点C重合,
故选:B.
【点睛】本题考查抛物线与y轴的交点,旋转的性质、勾股定理及锐角三角函数,根据抛物线求得顶点坐标,从而确定旋转角度是解题的关键.
6.如图,在中,,,点从点出发沿方问以向点匀速运动,过点作于点.以所在直线为对称轴,将折叠,点的对应点为,移动过程中与重叠部分的面积为,运动时间为,则与之间函数关系的图象大致是( )
A. B. C. D.
【答案】A
【分析】分两种情况讨论:①当时,,可以求出抛物线解析式,从而得到函数图像;②当时,,可以求出抛物线解析式,从而得到函数图像.
【详解】解:∵,,
∴当点D在中点时,和B重合,
∵,,
∴,
∴,
∴,
∵点速度是,运动时间为,
∴,
∴,
①当时,
由题意可得:,
此时,S与之间函数关系的图像是顶点在原点,开口向上的抛物线;
②当时,如图所示,
此时,
∵,,
∴,,
∵,
同理可得:,
∴,
∴当时,S有最大值,最大值为2,
此时,S与之间函数关系的图象是开口向下的抛物线,且当时,S有最大值,
故选:A.
【点睛】本题考查动点问题的函数图像,关键是分段求出S与之间函数解析式.
7.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A.B.C.D.
【答案】C
【分析】根据抛物线与x轴的两个交点坐标可得抛物线的对称轴为直线,再根据顶点坐标设解析式为,把代入求出a,即可得到解析式.
【详解】解:由二次函数的图象可得,抛物线与x轴的交点坐标为和,
∴对称轴为,
∵桥墩的高度为,
∴抛物线的顶点坐标为,
设抛物线的解析式为,
把代入上式得,,
∴,
∴该抛物线的表达式为,
即,
故选:C.
【点睛】本题考查了二次函数的实际应用,根据函数图象反映的信息求出解析式是解题的关键.
8.老师设计了“谁是卧底”游戏,用合作的方式描述一个二次函数的图象性质,其中,为常数,甲说:该二次函数的对称轴是直线;乙说:函数的最小值为;丙说:是方程的一个根;丁说:该二次函数的图象与轴交于.若四个描述中,只有“卧底”的描述是假命题,则“卧底”是( )
A.甲B.乙C.丙D.丁
【答案】C
【分析】设甲乙正确,利用顶点时写出抛物线的解析式为,然后计算自变量为和对应的函数值,从而判断丙错误.
【详解】解:若甲乙正确,则抛物线的解析式为,即,
当时,,此时丙错误;
当时,,此时丁正确.
而其中有且仅有一个说法是错误的,
所以只有丙错误,则“卧底”是丙.
故选:C.
【点睛】本题考查了抛物线与轴的交点:把求二次函数(a,b,c是常数,与轴的交点坐标问题转化为解关于的一元二次方程.也考查了二次函数的性质.
二、填空题
9.掷实心球是安徽省高中阶段学校招生体育考试的选考项目.如图是某学生投实心球,出手后实心球沿一段抛物线为常数,运行,当运行到最高点时,运行高度,水平距离.
(1)当出手高度为时, ;
(2)若实心球落地水平距离不小于,且不超过,则的取值范围是 .
【答案】
【分析】此题考查了二次函数的实际应用,解题的关键是熟练掌握二次函数的性质及其应用;
()利用待定系数法求出解析式即可;
()设,根据当时,,时,即可求出的取值范围.
【详解】解:()设,
将代入可得,
解得,
故答案为:;
(2)设,
若落地水平距离不小于,
则当时,,代入得,解得;
当时,,代入得,解得,
综上所述,.
10.已知拋物线与直线相交于点(点在点右侧),且.
(1)的值是 .
(2)直线与抛物线相交于点,与直线相交于点,.若随的增大而增大,则的取值范围是 .
【答案】 2
【分析】本题考查了二次函数的图象与性质,数形结合是解答本题的关键.
(1)先求出拋物线与直线交点横坐标,然后根据即可求出的值;
(2)设,,表示出的长,然后利用二次函数的性质求解即可.
【详解】解:(1)当时,,
解得,
,
即;
(2)当时,拋物线为,点,点,顶点为.
直线与轴交于点.
设,,
则,
∵当时,随的增大而增大,
∴,
解得.
11.如图①,是可移动的灌溉装置,以水平地面方向为x轴,点O为原点建立直角坐标系,点A在y轴上,如图②所示.其水柱的高度y(单位:m)与水柱距喷水头的水平距离x(单位:m)近似满足函数关系式.在图②中,若水柱在某一个高度时总对应两个不同的水平位置,则x的取值范围是 .
【答案】且
【分析】根据题意可先求出点的坐标,然后求出当时对应的值,即可得出水柱的水平距离的取值范围,然后求出顶点坐标和对称轴,再求出点关于对称轴对称的点,根据当水柱在某一个高度时,总对应两个不同的水平位置,即可得出的取值范围.
【详解】解:由题意可得:当时,,
,
当时,即,
解得:,,
水柱的水平距离的取值范围为:,
,
顶点坐标为,对称轴,
点关于对称轴对称的点为,
当水柱在某一个高度时,总对应两个不同的水平位置,
的取值范围为:且;
故答案为:且.
【点睛】本题考查的主要是二次函数的应用,解题关键是求出点关于对称轴对称的点以及顶点坐标.
12.在平面直角坐标系中,对封闭图形和不重合的两点,给出如下定义:点关于点的中心对称点为,若点在图形内(包含边界),则称图形为点经点投射的“靶区”.如图,拋物线与轴的交点A,位于原点两侧(点A在点的左侧),且,则抛物线的函数表达式为 ,记轴上方的拋物线与轴所围成的封闭图形为,点为轴上一动点,若直线上存在点,使得图形为点经点投射的“靶区”,则的取值范围是 .
【答案】 ; 且.
【分析】由,以及抛物线的对称轴,可得出点的坐标,进而求出函数表达式;求出直线关于轴的对称直线,再由对称直线与封闭图象的交点,可求出的取值范围.
【详解】解:由题知,
抛物线的对称轴为,
令,又,两点关于对称,
所以,则.
所以,.
又,
所以,得.
故.
将点坐标代入抛物线解析式得,,则.
所以抛物线的函数表达式为.
直线关于轴的对称直线为,
记直线与封闭区域的交点为,,
则,解得或.
故.
所以的取值范围是且.
故答案为:,且.
【点睛】本题考查二次函数的图象和性质,利用直线关于轴的对称直线是解题的关键.
13.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
【答案】/
【分析】利用待定系数法求出抛物线解析式,设,求出,即可得到矩形窗户的宽的长.
【详解】解:由题意可知,、、,
设抛物线解析式为,
,解得:
抛物线解析式为,
点G、H在边上,且,
、,
四边形是矩形,
设,
点在抛物线上,
,
,
故答案为:.
【点睛】本题考查了坐标与图形,待定系数法求函数解析式,矩形的性质,二次函数的性质等知识,求出二次函数解析式,掌握二次函数的性质是解题关键.
14.某游乐园要建造一个直径为的圆形喷水池,计划在喷水池的周边安装一圈喷水头,使喷出的水柱距池中心处达到最高,高度为.以水平方向为轴,喷水池中心为原点建立直角坐标系如图,若要在喷水池中心的正上方设计挡板(),使各方向喷出的水柱擦挡板后,汇合于喷水池中心装饰物M处,挡板所在直线的表达式为,则抛物线l的表达式为 ,n的值为
【答案】
【分析】运用待定系数法可求出抛物线的解析式,再与直线联立方程,令可求出的值.
【详解】解:设抛物线的解析式为,
根据题意得,在抛物线上,
∴,
解得,,
∴抛物线的解析式为,
与直线联立方程,得:
,
整理得:,
∵直线与抛物线有唯一公共点,
∴
解得,;
帮答案为:;.
【点睛】本题主要考查了函数图象与性质,正确求出抛物线的解析式是解答本题的关键.
15.如图,抛物线与y轴交于点A,过的中点作轴,交抛物线于B、C两点(点B在C的左边),连接、,若将向上平移使得B、C两点恰好落在抛物线上,则点O平移后的坐标为 .
【答案】
【分析】先求出,从而可得点和点的坐标,再设点平移后的对应点分别为点,则点的横坐标为,点的横坐标为,代入函数解析式可得的纵坐标,从而可得的中点向上平移的距离,由此即可得.
【详解】解:抛物线与轴交于点,
,
过的中点作轴,
点和点的纵坐标均为,
当时,则,解得,
,
如图,设点平移后的对应点分别为点,
则点的横坐标为,点的横坐标为,
当时,,
则的中点向上平移了个单位长度,
所以点也向上平移了个单位长度,
所以点平移后的坐标为,
故答案为:.
【点睛】本题考查了二次函数的图象与性质、点坐标的平移,熟练掌握二次函数的图象与性质是解题关键.
16.如图,在平面直角坐标系中,二次函数的图象与坐标轴相交于A,B,C三点,连接,.已知点E坐标为,点D在线段上,且.则四边形面积的大小为 .
【答案】
【分析】根据二次函数的解析式求出A,B,C三点的坐标,然后再求出所在直线的解析式,设,根据,求出D点坐标,再利用割补法即可求出四边形的面积.
【详解】解:二次函数的图象与坐标轴相交于A,B,C三点;
,,;
容易求出所在直线的解析式为;
设,
,
;
;
;,;
;
故答案为.
【点睛】本题考查了二次函数综合问题,涉及到了求二次函数与坐标轴的交点,利用待定系数法求函数解析式以及利用割补法求不规则图形的面积,熟练掌握二次函数的综合知识是解题的关键.
三、解答题
17.已知抛物线与x轴负半轴交于点A,与y轴交于点B.现将抛物线平移,使平移后的抛物线过点B和点.
(1)求抛物线的表达式;
(2)点为抛物线上一点,过点P作y轴平行线,交直线于点M,过点P作x轴平行线,交y轴于点N,当与相似时,求点P坐标.
【答案】(1)
(2)或
【分析】(1)先求出点B的坐标,然后用待定系数法求抛物线的表达式;
(2)先求出中,的长,,,再根据相似三角形的性质,分两种情况分别列出方程,并求解m的值,即可得到答案.
【详解】(1)令,则,
所以点B的坐标为,
设抛物线的表达式为,
将B、C两点的坐标代入得,
解得,
所以抛物线的表达式为;
(2)令,则,
解得,,
所以点A的坐标为,
在中,,,
点P的坐标为,,
设直线的解析式为,
则,
解得,
所以直线的解析式为,
所以点M的坐标为,
所以,
当时,,
即,
解得,
所以点P坐标为或;
当时,,
即,
解得,
所以点P坐标为;
综上所述,点P坐标为或.
【点睛】本题考查了二次函数的相似三角形问题,二次函数的平移,用待定系数法求二次函数的解析式,相似三角形的性质,求一次函数的解析式,分两种情况求点P的坐标是解题的关键.
18.湘雅公园人工湖上有一座拱桥,横截面呈抛物线形状,如图所示,现对此展开研究:跨度为4米,桥墩露出水面的高度为米,在距点A水平距离为2米的地点,拱桥距离水面的高度为米,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是横截水面,是拱桥距水面的高度.
(1)求抛物线的表达式;
(2)公园欲开设游船项目,为安全起见,公园要在水面上的C、D两处设置航行警戒线,并且,要求游船能从C、D两点之间安全通过,则C处距桥墩的距离CE至少为多少米?
【答案】(1);
(2)C处距桥墩的距离至少为米.
【分析】本题主要考查了二次函数的应用,审清题意、掌握数形结合思想是解题的关键.
(1)先确定抛物线的顶点坐标,然后用代入消元法即可解答;
(2)令可得,然后解二元一次方程即可解答.
【详解】(1)解:∵为4米,在距点A水平距离为2米的地点,拱桥距离水面的高度为2.88米,
∴抛物线顶点为,
设抛物线的表达式为,
将代入得:,解得.
∴抛物线的表达式为.
(2)解:在中,令可得:
,
解得:(舍去)或,
∴C处距桥墩的距离至少为米.
19.在平面直角坐标系中,二次函数的图象如图所示,该抛物线的顶点为,且与轴的交点为,连接过点作轴的平行线与抛物线交于另一点,过点作的垂线.
(1)当时,求的长;
(2)如图,延长交于点,请用含的代数式表示的面积;
(3)如图,点在抛物线第一象限的图象上且位于点的左侧,连接并延长交于点,过点作垂直于,垂足为点,连接求证:.
【答案】(1)
(2)
(3)证明见解析
【分析】本题考查二次函数的图象及性质,待定系数法求函数的解析式,熟练掌握两条直线的值相等,则两直线平行是解题的关键.
(1)根据顶点式解析式求出点坐标,令,求出值可得点坐标,利用两点间距离公式求出的长即可;
(2)分别用表示出、、的坐标,可表示出的长,再用待定系数法求直线的解析式,表示出点坐标,从而求出的长,即可求的面积;
(3)设,用待定系数法先求直线的解析式,从而求出点的坐标,再用待定系数法求出直线的解析式,从而判断直线与是平行的即可.
【详解】(1)解:当时,,
∵该抛物线的顶点为,
∴,
当时,,
∴,
.
(2)∵,
∴,
当时,,
∴,
∵轴,
∴,
∴,
设直线的解析式为,
∴,
解得:,
∴直线的解析式为,
当时,,
∴,
∴,
∴.
(3)设,直线的解析式为,
∴,
解得,
∴直线的解析式为,
当时,
∴,
∵,
∴同理可求直线的解析式为,
∵直线的解析式为,
∴.
20.综合实践
(1)填空:在上图中位似中心是点________;________多边形是特殊的________多边形.(填“位似”或“相似”)
(2)在平面直角坐标系中(如下图),二次函数的图像与x轴交于点A,点B是此函数图像上一点(点A、B均不与点O重合),已知点B的横坐标与纵坐标相等,以点O为位似中心,相似比为,将缩小,得到它的位似.
①画出,并求经过O、、三点的抛物线的表达式;
②直线与二次函数的图像交于点M,与①中的抛物线交于点N,请判断和是否为位似三角形,并根据新定义说明理由.
【答案】(1)P;位似;相似
(2)①图形见解析;;②和为位似三角形,理由见解析
【分析】(1)根据位似图形的定义,即可求解;
(2)①根据位似图形的定义,画出图形,再求出、的坐标,即可求解;②过点M作轴于点D,过点N作轴于点C,联立求出点M,N的坐标,可得,从而得到,进而得到,再由点的坐标为,点A的坐标为,可得,然后根据新定义,即可求解.
【详解】(1)解:在上图中位似中心是点P;位似多边形是特殊的相似多边形.
故答案为:P;位似;相似
(2)解:①如图,即为所求;
令,则,
解得:或0,
∴点A的坐标为,
设点B的坐标为,
∴,解得:或0,
∴点B的坐标为,
∵以点O为位似中心,相似比为,将缩小,得到它的位似,
∴点的坐标为,点的坐标为,
设经过O、、三点的抛物线的表达式为,
把点,,代入得:
,解得:,
∴经过O、、三点的抛物线的表达式为,
②和为位似三角形,理由如下:
如图,过点M作轴于点D,过点N作轴于点C,
联立得: ,解得:或,
∴点M的坐标为,
∴,,,
同理点N的坐标为,
∴,,
∴,
∵,
∴,
∴,
∵点的坐标为,点A的坐标为,
∴,
∴,
∴和为位似三角形.
【点睛】本题主要考查了相似三角形的判定和性质,二次函数的综合应用,理解新定义,利用数形结合思想解答是解题的关键.九年级第一学期教材第2页
结合教材图形给出新定义
对于下图中的三个四边形,通常可以说,缩小四边形,得到四边形;放大四边形,得到四边形.
图形的放大或缩小,称为图形的放缩运动.将一个图形放大或缩小后,就得到与它形状相同的图形.图中,四边形和四边形都与四边形形状相同.我们把形状相同的两个图形说成是相似的图形,或者就说是相似形.
如图,对于两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形,这个点就是位似中心.
相关试卷
这是一份2024年中考数学【高分·突破】考点01实数及其运算(原卷版+解析),共21页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份中考数学总复习专题06分式方程及其应用(10个高频考点)(强化训练)(全国版)(原卷版+解析),共40页。
这是一份中考数学总复习专题06分式方程及其应用(10个高频考点)(举一反三)(全国版)(原卷版+解析),共32页。









