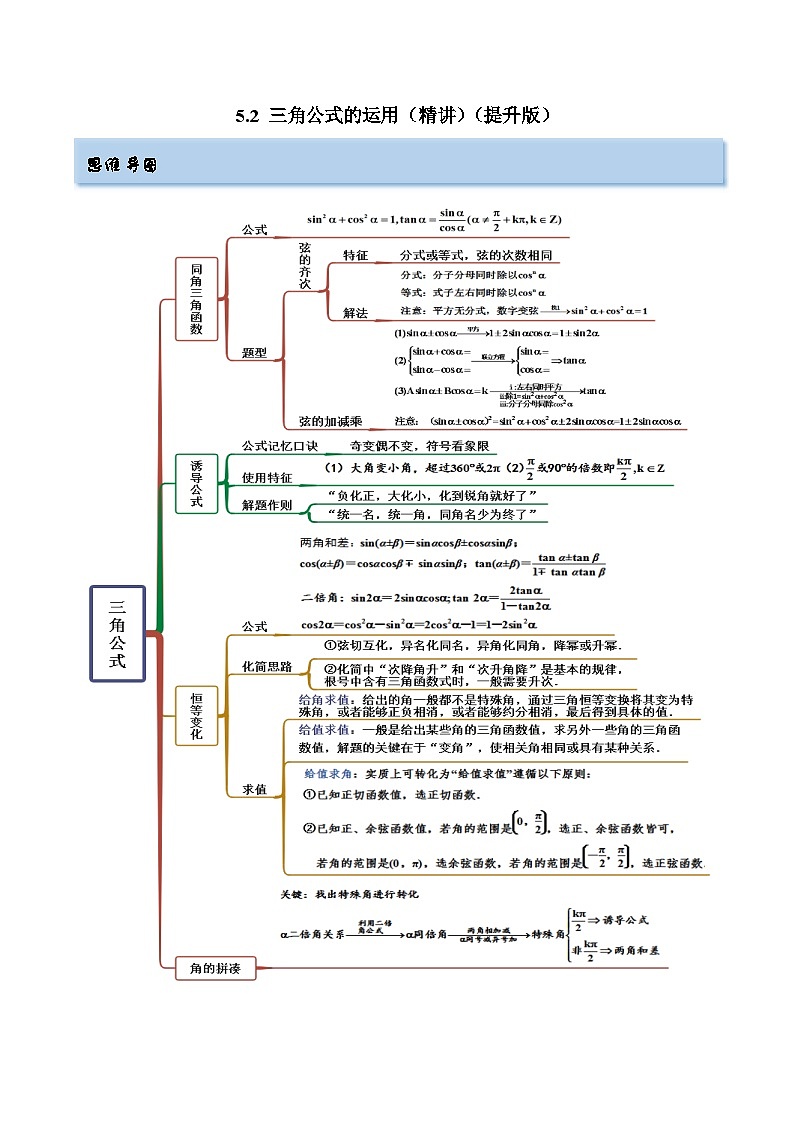
备战2024年高考数学一轮复习5.2三角公式的运用(精讲)(原卷版+解析)

这是一份备战2024年高考数学一轮复习5.2三角公式的运用(精讲)(原卷版+解析)，共21页。试卷主要包含了公式的基本运用，角的拼凑，恒等变化，三角公式与其他知识综合运用等内容，欢迎下载使用。

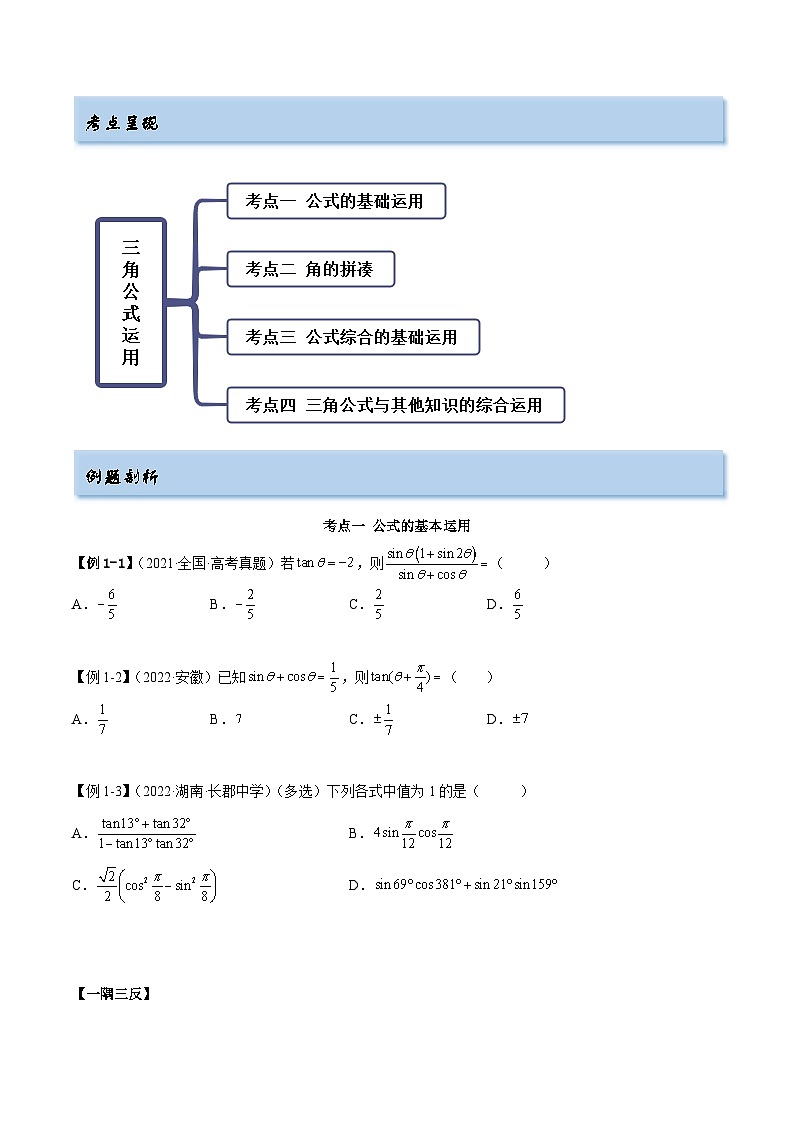
考点呈现
例题剖析
考点一 公式的基本运用
【例1-1】（2021·全国·高考真题）若，则（ ）
A．B．C．D．
【例1-2】（2022·安徽）已知，则（ ）
A．B．C．D．
【例1-3】（2022·湖南·长郡中学）（多选）下列各式中值为1的是（ ）
A．B．
C．D．
【一隅三反】
1．（2021·全国·高考真题（文））若，则（ ）
A．B．C．D．
2．（2022·江苏南通·模拟预测）在△ABC中，若，则（ ）
A．B．C．D．
3．（2021·全国·课时练习）（多选）下列等式成立的是（ ）
A． B．
C． D．
4．（2022·江苏·泗阳县实验高级中学）（多选）已知，则（ ）
A．B．
C．D．
5．（2022·湖南省隆回县第二中学）已知，则（ ）
A．-B．-C．D．
考点二 角的拼凑
【例2-1】（2022·四川成都）若，，则的值为（ ）
A．B．C．D．
【例2-2】（2021·安徽·高三阶段练习（理））已知，则（ ）
A．B．C．D．
【例2-3】（2022·江苏）已知，，且，，则（ ）
A．B．C．D．
【一隅三反】
1．（2022·福建南平）若，则（ ）
A．B．C．D．
2．（2022·山东·聊城二中高三开学考试）已知，且，则的值为（ ）
A．B．
C．D．
3．（2021·江苏·高三阶段练习）已知，则（ ）
A．B．C．D．
4．（2021·江苏·苏州市相城区陆慕高级中学高三阶段练习）已知，，，则（ ）
A．B．
C．D．
5．（2022·全国·课时练习）已知，，，则________，________．
考点三 恒等变化
【例3】（2022·湖北武汉·高三期末）计算（ ）
A．1B．﹣1C．D．
【一隅三反】
1．（2022·全国·高三专题练习）（ ）
A．B．C．D．
2．（2022·河北省唐县第一中学高三阶段练习）已知，则（ ）
A．B．C．D．
3．（2022·西藏）求的值（ ）
A．1B．3C．D．
考点四 三角公式与其他知识综合运用
【例4-1】（2022·全国·模拟预测（文））已知在处的切线倾斜角为，则的值为（ ）
A．7B．C．5D．-3
【例4-2】（2022·福建·厦门双十中学）如图1，正方形ABCD的边长为2，点M为线段CD的中点. 现把正方形纸按照图2进行折叠，使点A与点M重合，折痕与AD交于点E，与BC交于点F. 记，则_______.
【一隅三反】
1．（2022·湖南·长沙市明德中学高三阶段练习）已知，设，，，则a，b，c的大小关系是（ ）
A．B．C．D．
2．（2021·河北·张家口市宣化第一中学）在直角坐标系中，的顶点，，，且的重心的坐标为，__________.
3.，则实数的取值范围为______.
5.2 三角公式的运用（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 公式的基本运用
【例1-1】（2021·全国·高考真题）若，则（ ）
A．B．C．D．
【答案】C
【解析】将式子进行齐次化处理得：
．故选：C．
【例1-2】（2022·安徽）已知，则（ ）
A．B．C．D．
【答案】C
【解析】因为，所以，即，
当时，即，则，
所以，则，所以；
当时，即，则，
所以，则，所以；综上：，
故选：C
【例1-3】（2022·湖南·长郡中学）（多选）下列各式中值为1的是（ ）
A．B．
C．D．
【答案】ABD
【解析】A：，符合题意；
B：，符合题意；
C：，不符合题意：
D： 符合题意.
故选：ABD．
【一隅三反】
1．（2021·全国·高考真题（文））若，则（ ）
A．B．C．D．
【答案】A
【解析】，
，，，解得，
，.故选：A.
2．（2022·江苏南通·模拟预测）在△ABC中，若，则（ ）
A．B．C．D．
【答案】A
【解析】因为，
所以，所以，
，故选：A．
3．（2021·全国·课时练习）（多选）下列等式成立的是（ ）
A． B．
C． D．
【答案】AD
【解析】对于A，，A正确；
对于B，，B错误；
对于C，，C错误；
对于D，，D正确.故选：AD.
4．（2022·江苏·泗阳县实验高级中学）（多选）已知，则（ ）
A．B．
C．D．
【答案】BCD
【解析】依题意，，
，，
，所以或，
，或，（舍去），或，所以，
，.所以A选项错误，BCD选项正确.故选：BCD
5．（2022·湖南省隆回县第二中学）已知，则（ ）
A．-B．-C．D．
【答案】C
【解析】由，，
两边平方后相加得，
即,得，所以,故选:C.
考点二 角的拼凑
【例2-1】（2022·四川成都）若，，则的值为（ ）
A．B．C．D．
【答案】D
【解析】因为，所以，又因为，所以，
所以.故选：D.
【例2-2】（2021·安徽·高三阶段练习（理））已知，则（ ）
A．B．C．D．
【答案】B
【解析】因，所以.故选：B
【例2-3】（2022·江苏）已知，，且，，则（ ）
A．B．C．D．
【答案】A
【解析】且，，.
又，，.
当时，
，
，，不合题意，舍去；
当，同理可求得，符合题意.
综上所述：.
故选：.
【一隅三反】
1．（2022·福建南平）若，则（ ）
A．B．C．D．
【答案】A
【解析】由题设，，则，
又.故选：A
2．（2022·山东·聊城二中高三开学考试）已知，且，则的值为（ ）
A．B．
C．D．
【答案】C
【解析】由，而，∴，
∴.故选：C.
3．（2021·江苏·高三阶段练习）已知，则（ ）
A．B．C．D．
【答案】A
【解析】，
故选：A.
4．（2021·江苏·苏州市相城区陆慕高级中学高三阶段练习）已知，，，则（ ）
A．B．
C．D．
【答案】D
【解析】因为，，所以两式平方相加得，
即，
又因为，所以，即，，
将代入，得，即，
所以，∴.故选：D.
5．（2022·全国·课时练习）已知，，，则________，________．
【答案】
【解析】因，则，而，则有，
又，即，而，则，
所以，
而，于是得，所以，.故答案为：；
考点三 恒等变化
【例3】（2022·湖北武汉·高三期末）计算（ ）
A．1B．﹣1C．D．
【答案】B
【解析】
故选：B
【一隅三反】
1．（2022·全国·高三专题练习）（ ）
A．B．C．D．
【答案】D
【解析】
，故选：D
2．（2022·河北省唐县第一中学高三阶段练习）已知，则（ ）
A．B．C．D．
【答案】D
【解析】因为，所以.所以，
则，即，解得.故选：D
3．（2022·西藏）求的值（ ）
A．1B．3C．D．
【答案】D
【解析】
．故选：D．
考点四 三角公式与其他知识综合运用
【例4-1】（2022·全国·模拟预测（文））已知在处的切线倾斜角为，则的值为（ ）
A．7B．C．5D．-3
【答案】B
【解析】因为，所以，
所以.
故选：B
【例4-2】（2022·福建·厦门双十中学）如图1，正方形ABCD的边长为2，点M为线段CD的中点. 现把正方形纸按照图2进行折叠，使点A与点M重合，折痕与AD交于点E，与BC交于点F. 记，则_______.
【答案】
【解析】设，则，在中，，所以，
即，解得，所以，所以在中，，
则，
又，
所以.故答案为：
【一隅三反】
1．（2022·湖南·长沙市明德中学高三阶段练习）已知，设，，，则a，b，c的大小关系是（ ）
A．B．C．D．
【答案】C
【解析】方法一：∵，
∴，．
方法二：令，则．
故选：C.
2．（2021·河北·张家口市宣化第一中学）在直角坐标系中，的顶点，，，且的重心的坐标为，__________.
【答案】
【解析】由题意知：，
∴，即，
∴，
，
将两式相加，得：，
∴.
故答案为：.
3.，则实数的取值范围为______.
【答案】
【解析】
，
设，，，
则，
如图，
，当且仅当三点共线且点在之间时等号成立，
又，故的最大值为，
因为存在实数使得
所以
即
故答案为：