备战2024年高考数学一轮复习7.4空间距离(精练)(原卷版+解析)

这是一份备战2024年高考数学一轮复习7.4空间距离(精练)(原卷版+解析)，共34页。试卷主要包含了线面距等内容，欢迎下载使用。
1.（2022·福建）在空间直角坐标系中，点，则到直线的距离为___．
2（2022·北京·二模）如图，已知正方体的棱长为1，则线段上的动点P到直线的距离的最小值为
3．（2022·广东）如图，在棱长为4的正方体中，E为BC的中点，点P在线段上，点Р到直线的距离的最小值为_______.
题组二 点面距
1．（2022·江苏）将边长为的正方形沿对角线折成直二面角，则点到平面的距离为___．
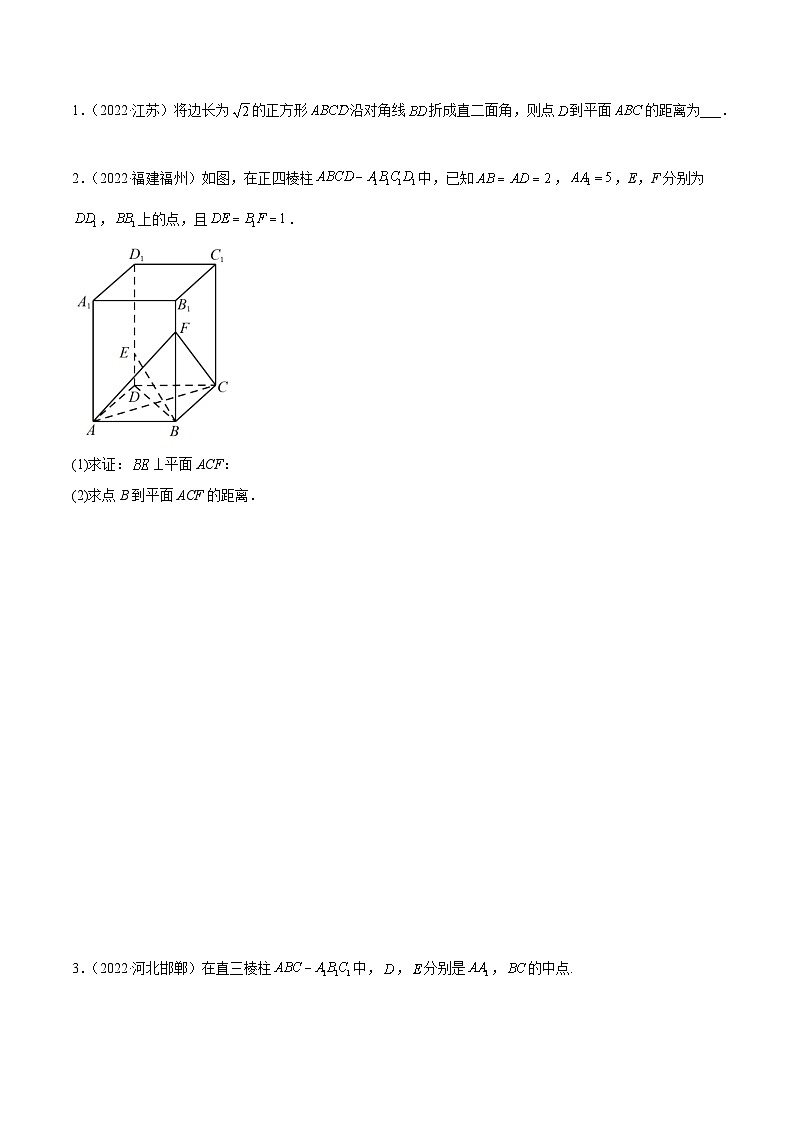
2．（2022·福建福州）如图，在正四棱柱中，已知，，E，F分别为，上的点，且．
(1)求证：平面ACF：
(2)求点B到平面ACF的距离．
3．（2022·河北邯郸）在直三棱柱中，，分别是，的中点.
(1)求证：平面；
(2)若，，，求点到平面的距离.
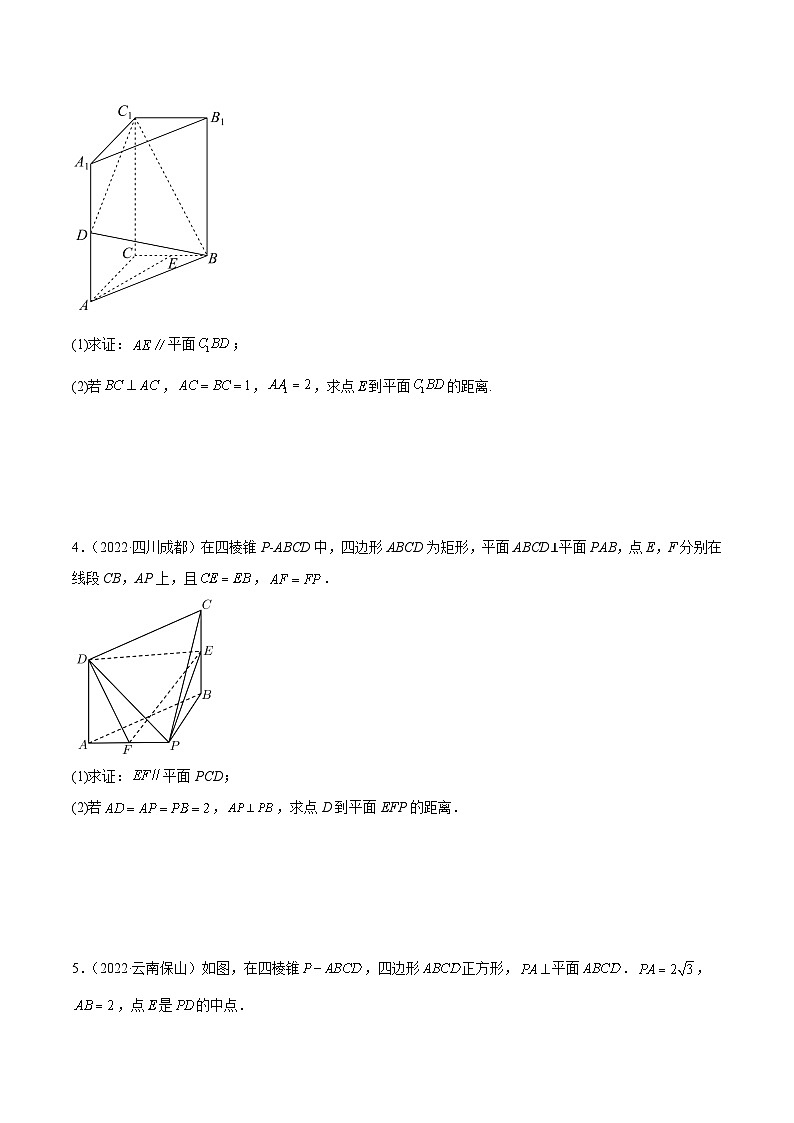
4．（2022·四川成都）在四棱锥P-ABCD中，四边形ABCD为矩形，平面ABCD⊥平面PAB，点E，F分别在线段CB，AP上，且，．
(1)求证：平面PCD；
(2)若，，求点D到平面EFP的距离．
5．（2022·云南保山）如图，在四棱锥，四边形正方形，平面．，，点是的中点．
(1)求证：平面；
(2)求点到平面的距离．
题组三 线线距
1．（2022·全国·课时练习）如图，多面体是由长方体一分为二得到的，，，，点D是中点，则异面直线与的距离是______．
2．（2022·福建）如图，在正方体中，AB＝1，M，N分别是棱AB，的中点，E是BD的中点，则异面直线，EN间的距离为______.
3．（2022·浙江）如图，正四棱锥的棱长均为2，点E为侧棱PD的中点．若点M，N分别为直线AB，CE上的动点，则MN的最小值为______．
4．（2022·湖北）如图，棱长为1的正方体ABCD-A1B1C1D1中，N是棱AD的中点，M是棱CC1上的点，且CC1=3CM，则直线BM与B1N之间的距离为____.
题组四 线面距
1．（2022·山东滨州）在棱长为的正方体中，直线BD到平面的距离为（ ）
A．B．C．D．
2．（2022·山西）如图，在正方体中，为的中点．
(1)证明：平面AD1E
(2)求直线到平面的距离；
3．（2022·云南·会泽县实验高级中学校）如图，在梯形ABCD中，，，，平面ABCD，且，点F在AD上，且．
(1)求点A到平面PCF的距离；
(2)求AD到平面PBC的距离．
题组五 面面距
1．（2022·江苏）已知正方体的棱长为，则平面与平面的距离为（ ）
A．B．C．D．
2．（2022·云南）如图，在棱长为1的正方体ABCD­A1B1C1D1中，E，F分别为棱AA1，BB1的中点，则A1B1到平面D1EF的距离是________．
3．（2022·上海）如图，在棱长为a的正方体中，E、F分别是、的中点．则点A和点的距离为______，点到棱BC的距离为______，点E到平面的距离为______，到平面AEFD的距离为______．
4．（2022·广东）在棱长为的正方体中，、、、分别为、、、的中点．
(1)求证：平面平面；
(2)求平面与平面之间的距离．
5．（2022·天津河北）如图，在直三棱柱中，，，，分别为，，的中点，点在棱上，且，，.
(1)求证：平面；
(2)求证：平面平面；
(3)求平面与平面的距离.
6．（2022·哈尔滨）已知正方体的棱长均为1.
(1)求到平面的距离；
(2)求平面与平面之间的距离.
7.4 空间距离（精练）（提升版）
题组一 点线距
1.（2022·福建）在空间直角坐标系中，点，则到直线的距离为___．
【答案】
【解析】依题意得，则到直线的距离为故答案为：
2（2022·北京·二模）如图，已知正方体的棱长为1，则线段上的动点P到直线的距离的最小值为
【答案】
【解析】如图建立空间直角坐标系，则，
设，则，
∴动点P到直线的距离为
，当时取等号，
即线段上的动点P到直线的距离的最小值为.
3．（2022·广东）如图，在棱长为4的正方体中，E为BC的中点，点P在线段上，点Р到直线的距离的最小值为_______.
【答案】
【解析】在正方体中，建立如图所示的空间直角坐标系，
则，，
因点P在线段上，则，，
，向量在向量上投影长为，
而，则点Р到直线的距离
，当且仅当时取“=”，
所以点Р到直线的距离的最小值为.
故答案为：
题组二 点面距
1．（2022·江苏）将边长为的正方形沿对角线折成直二面角，则点到平面的距离为___．
【答案】
【解析】记AC与BD的交点为O，图1中，由正方形性质可知，
所以在图2中，，所以，即
如图建立空间直角坐标系，易知
则
则
设为平面ABC的法向量，
则，取，得
所以点到平面的距离
故答案为：
2．（2022·福建福州）如图，在正四棱柱中，已知，，E，F分别为，上的点，且．
(1)求证：平面ACF：
(2)求点B到平面ACF的距离．
【答案】(1)证明见详解.(2).
【解析】（1）以为坐标原点，为轴，为轴，为轴建立空间直角坐标系，如下图所示：
则,设面的一个法向量为，，可得，即，不妨令则,平面.
（2），则点到平面的距离为.
3．（2022·河北邯郸）在直三棱柱中，，分别是，的中点.
(1)求证：平面；
(2)若，，，求点到平面的距离.
【答案】(1)详见解析(2)
【解析】（1）连结交于点，连结，因为点分别是的中点，所以，且，所以，即四边形是平行四边形，所以，且平面，平面，所以平面；
（2）因为，则,,，所以，所以，,因为，且，，所以平面，因为，所以点到平面的距离为1，，根据等体积转化可知，即，解得：，所以点到平面的距离为.
4．（2022·四川成都）在四棱锥P-ABCD中，四边形ABCD为矩形，平面ABCD⊥平面PAB，点E，F分别在线段CB，AP上，且，．
(1)求证：平面PCD；
(2)若，，求点D到平面EFP的距离．
【答案】(1)证明见解析(2)
【解析】(1)证明：如图，取的中点，连接，．
在中，点，分别为，的中点，
∴且．
在矩形中，点为的中点，
∴且，∴且．
∴.四边形是平行四边形，
∴．
又∵平面，平面，
∴平面．
(2)解：∵四边形是矩形，
∴．
∵平面平面，平面平面，平面，
∴平面，又平面，∴，
∵，，，平面.
∴平面，即就是点到平面的距离．
∵，平面，平面，所以平面，
∴点到平面的距离等于点到平面的距离．
又∵，
∴．
同理可证平面，即，
且，， 平面，
∴平面.
∴，即．
∴，
∴点到平面的距离为．
5．（2022·云南保山）如图，在四棱锥，四边形正方形，平面．，，点是的中点．
(1)求证：平面；
(2)求点到平面的距离．
【答案】(1)证明见解析(2)
【解析】(1)证明：连接交于点，连接，
底面为正方形，为中点，
点是的中点，，
平面，平面，
平面．
(2)解：因为平面，平面，所以，又四边形为正方形，
所以，又，平面，
所以平面，平面，所以，
又点是的中点，，，所以，，
，，
所以，
设点到平面的距离为，则，即，
即，解得，
即点到平面的距离为.
题组三 线线距
1．（2022·全国·课时练习）如图，多面体是由长方体一分为二得到的，，，，点D是中点，则异面直线与的距离是______．
【答案】
【解析】以为坐标原点，分别以，,为轴，轴，轴建立空间直角坐标系，则,,,,
∴,,
设是，的公垂线方向上的单位向量，
则，即①，
，即②，
易知③，
联立解得，，或，，；
不妨取，
又∵,
则异面直线与的距离，
故答案为：.
2．（2022·福建）如图，在正方体中，AB＝1，M，N分别是棱AB，的中点，E是BD的中点，则异面直线，EN间的距离为______.
【答案】
【解析】
以为原点，的方向为轴建立空间直角坐标系，易知，
，设同时垂直于，由，令，得，
又，则异面直线，EN间的距离为.
故答案为：.
3．（2022·浙江）如图，正四棱锥的棱长均为2，点E为侧棱PD的中点．若点M，N分别为直线AB，CE上的动点，则MN的最小值为______．
【答案】
【解析】
建立如图所示的空间直角坐标系，则有：
，，，，，
可得：
设，且
则有：，
可得：
则有：
故
则当且仅当时，
故答案为：
4．（2022·湖北）如图，棱长为1的正方体ABCD-A1B1C1D1中，N是棱AD的中点，M是棱CC1上的点，且CC1=3CM，则直线BM与B1N之间的距离为____.
【答案】
【解析】正方体的棱长为1，如图，以D为坐标原点，所在方向分别为轴正方向建立空间直角坐标系，
则B(1，1，0)，B1(1，1，1)，，，∴=(0，0，1)，，.
设直线BM与B1N的公垂线方向上的向量，由，，
得，令x=2，则z=6，y=-7，∴，
设直线BM与B1N之间的距离为d，则d===.故答案为：.
题组四 线面距
1．（2022·山东滨州）在棱长为的正方体中，直线BD到平面的距离为（ ）
A．B．C．D．
【答案】B
【解析】因为,平面,平面,因此平面,故直线BD到平面的距离即为点到平面的距离；
为边长为2的等边三角形，故，,
设点到平面的距离为，由等体积法可得,即,故选:B
2．（2022·山西）如图，在正方体中，为的中点．
(1)证明：平面AD1E
(2)求直线到平面的距离；
【答案】(1)证明见解析(2)
【解析】（1），，四边形为平行四边形，，面，面，平面．
（2）如图建立空间直角坐标系，设正方体的棱长为，
则，，，，，平面，直线到平面的距离即为点到平面的距离，所以，，，设平面的一个法向量为，则，取，得，，直线到平面的距离为.
3．（2022·云南·会泽县实验高级中学校）如图，在梯形ABCD中，，，，平面ABCD，且，点F在AD上，且．
(1)求点A到平面PCF的距离；
(2)求AD到平面PBC的距离．
【答案】(1)；(2).
【解析】(1)连接AC，因为平面ABCD，又平面ABCD，
∴PA⊥CF，又，，
∴平面PAC，又平面PFC，
∴平面PFC⊥平面PAC，平面PFC⊥平面PAC=PC，
过点A作AH⊥PC于H，则AH⊥平面PFC，
故AH即为所求，
∵在梯形ABCD中，，，，，
∴，
∴在中，，
∴，即点A到平面PCF的距离为；
(2)∵，平面PBC，平面PBC，
∴平面PBC，
过点A作AE⊥PB于E，又因为平面ABCD，则BC，
又AB⊥BC，，
∴BC⊥平面PBA，则BC⊥AE，又
∴AE⊥平面PBC，即AE的长为AD到平面PBC的距离，
在等腰直角三角形PAB中，，
∴，
故AD到平面PBC的距离为.
题组五 面面距
1．（2022·江苏）已知正方体的棱长为，则平面与平面的距离为（ ）
A．B．C．D．
【答案】C
【解析】由正方体的性质，∥,∥，，，
易得平面平面，
则两平面间的距离可转化为点B到平面的距离．
以D为坐标原点，DA，DC，所在的直线分别为x轴、y轴、z轴
建立空间直角坐标系，
则，，，，，
所以，，，．
连接，由，，且，可知平面，得平面的一个法向量为，则两平面间的距离．
故选：C
2．（2022·云南）如图，在棱长为1的正方体ABCD­A1B1C1D1中，E，F分别为棱AA1，BB1的中点，则A1B1到平面D1EF的距离是________．
【答案】
【解析】因为，且面，所以，面，则A1B1到平面D1EF的距离为到面的距离，且明显可见，面，对于三棱锥，有，设到面的距离为，
由题意得，，，，在中，得到，
，所以，
，化简得
，
进而可得，
故答案为：
3．（2022·上海）如图，在棱长为a的正方体中，E、F分别是、的中点．则点A和点的距离为______，点到棱BC的距离为______，点E到平面的距离为______，到平面AEFD的距离为______．
【答案】 a
【解析】连接,
连接，在正方体中，平面，又平面
所以，即为点到棱BC的距离
取的中点，连接，则平面
所以为点E到平面的距离
E、F分别是、的中点，则 又，则
又平面AEFD, 平面AEFD，所以平面AEFD，
则点到平面AEFD的距离等于直线到平面AEFD的距离.
由平面,则平面,
又平面，所以平面平面，且平面平面
则过点作交直线于点，则平面
即为直线到平面AEFD的距离.
由, 则
故答案为：；； ；
4．（2022·广东）在棱长为的正方体中，、、、分别为、、、的中点．
(1)求证：平面平面；
(2)求平面与平面之间的距离．
【答案】(1)证明见解析(2)
【解析】(1)证明：因为、分别为、的中点，则．
又因为平面，平面，所以平面．
因为，，、分别为、的中点，则且，
所以，四边形为平行四边形，则，
平面，平面，所以，平面．
又因为，所以平面平面．
(2)解：连接分别交、于点、，则为的中点，且，
因为平面，平面，，
又因为，，平面，
因为平面平面，所以，平面，
所以线段的长度等于平面与平面之间的距离，
因为、分别为、的中点，则且，
且有，则，
因为正方体的棱长为，所以，
即平面与平面之间的距离为．
5．（2022·天津河北）如图，在直三棱柱中，，，，分别为，，的中点，点在棱上，且，，.
(1)求证：平面；
(2)求证：平面平面；
(3)求平面与平面的距离.
【答案】(1)见解析(2)见解析(3)
【解析】(1)证明：在直三棱柱中，
为的中点，，，
故，
因为，
所以，
又平面，平面，
所以，
又因，，
所以平面，
又平面，所以，
又，
所以平面；
(2)证明：取的中点，连接，
则为的中点，
因为，，分别为，，的中点，
所以，且，
所以四边形是平行四边形，
所以，所以，
又平面，平面，
所以平面，
因为，所以，
又平面，平面，
所以平面，
又因，平面，平面，
所以平面平面；
(3)
设，
因为平面，平面平面，所以平面，
所以即为平面与平面的距离，
因为平面，所以，
，
所以，
即平面与平面的距离为.
6．（2022·哈尔滨）已知正方体的棱长均为1.
(1)求到平面的距离；
(2)求平面与平面之间的距离.
【答案】(1)；(2).
【解析】(1)如图：

设到平面的距离为，正方体的棱长均为1，
且面.
,.

.
(2)

平面,平面.
故平面平面.
到平面的距离等于平面与平面之间的距离，设为.

即.
.