2024年广西贵港市中考数学二模试卷（含解析）

这是一份2024年广西贵港市中考数学二模试卷（含解析），共25页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．（3分）﹣2024的相反数是（ ）
A．2024B．C．﹣2024D．
2．（3分）据统计，2023年贵港市中考报名人数约为8万，数据8万用科学记数法可表示为（ ）
A．8×105B．0.08×106C．8×104D．0.8×105
3．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
4．（3分）实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（ ）
A．a＞0B．a＜bC．b﹣1＜0D．ab＞0
5．（3分）如图是一个正方体积木，它的每个面上都有一个数字，其中1的对面是6，2的对面是5，3的对面是4，现将积木沿着地面标志翻转，最后朝上的面的数字是（ ）
A．4B．3C．2D．5
6．（3分）如图，一束光从点C出发，经过平面镜AE反射后，沿与AB平行的射线DF射出（此时有∠∠1＝∠2），若测得∠3＝100°，则∠A等于（ ）
A．50°B．60°C．70°D．80°
7．（3分）任意掷一枚骰子，下列情况出现的可能性比较大的是（ ）
A．面朝上的点数是3
B．面朝上的点数是奇数
C．面朝上的点数小于2
D．面朝上的点数不小于3
8．（3分）把多项式m2﹣1分解因式得（ ）
A．（m+1）（m﹣1）B．m（m﹣1）
C．（m+1）2D．（m﹣1）2
9．（3分）“鸡兔同笼”是我国民间流传的诗歌形式的数学题：“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔”解决此问题，设鸡为x只，兔为y只，则所列方程组正确的是（ ）
A．B．
C．D．
10．（3分）如图，AB是圆O的直径，CD是圆O的弦，∠ABD＝69°，则∠C等于（ ）
A．29°B．21°C．31°D．62°
11．（3分）二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1，其中结论正确的为（ ）
A．abc＜0B．b2﹣4ac＝0C．a﹣b+c＞0D．4a+2b+c＜0
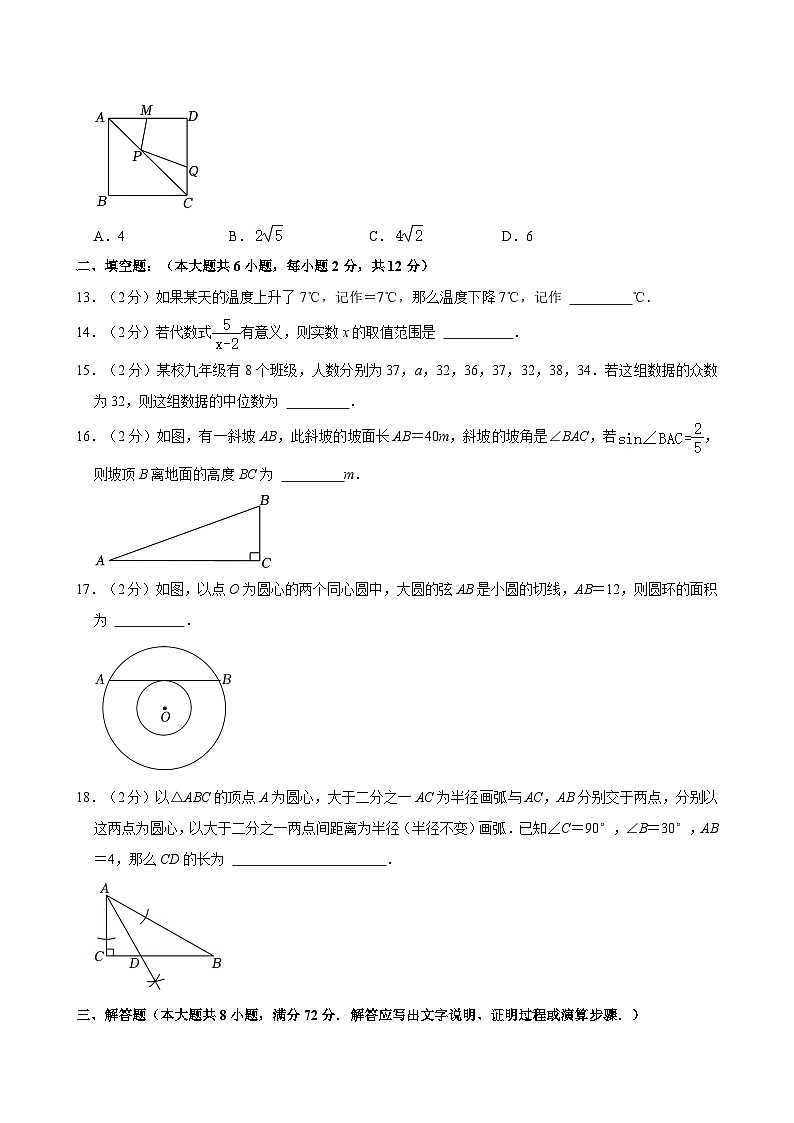
12．（3分）如图，正方形ABCD的边长为4点M是AD的中点，若动点P在对角线AC上，动点Q在CD边上，则PM+PQ的最小值是（ ）
A．4B．C．D．6
二、填空题：（本大题共6小题，每小题2分，共12分）
13．（2分）如果某天的温度上升了7℃，记作＝7℃，那么温度下降7℃，记作 ℃．
14．（2分）若代数式有意义，则实数x的取值范围是 ．
15．（2分）某校九年级有8个班级，人数分别为37，a，32，36，37，32，38，34．若这组数据的众数为32，则这组数据的中位数为 ．
16．（2分）如图，有一斜坡AB，此斜坡的坡面长AB＝40m，斜坡的坡角是∠BAC，若，则坡顶B离地面的高度BC为 m．
17．（2分）如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，AB＝12，则圆环的面积为 ．
18．（2分）以△ABC的顶点A为圆心，大于二分之一AC为半径画弧与AC，AB分别交于两点，分别以这两点为圆心，以大于二分之一两点间距离为半径（半径不变）画弧．已知∠C＝90°，∠B＝30°，AB＝4，那么CD的长为 ．
三、解答题（本大题共8小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
19．（9分）计算：．
20．（9分）解方程组：．
21．（9分）如图，已知AE∥BF，AC平分∠BAE．
（1）尺规作图：作∠ABF的平分线交AC于点O，交AE于点D；
（要求：保留作图痕迹，不写作法，标明字母）
（2）求证：△ABO≌△ADO．
22．（9分）某学校为了美化校园环境，打造绿色校园，计划用长为120米的篱笆来围成一个一面靠墙（墙足够长）的矩形花园，并用一道篱笆把花园分为A和B两块区域（如图所示）．（1）设垂直于墙的一边长为x米，则平行于墙的一边长为 米；
（2）请设计一个方案，使得花园的面积最大，并求出最大面积．
（3）在花园面积最大的条件下，A和B两块区域分别种植牡丹和芍药，每平方米种植2株，已知牡丹每株的售价为25元，芍药每株的售价为15元，学校计划购买这些植物的费用不超过5万元，求学校最多能购买多少株牡丹．
23．（9分）如图，点A，C均在⊙O上，OA⊥OC，⊙O外一点P在直线OC上，连接PA交⊙O于点B，作点B关于PC的对称点D，以点D为顶点作∠ADE＝∠PAO，点E在PA上．
（1）求证：ED是⊙O的切线；
（2）若AD平分∠PAO，，求DE的长．
24．（9分）甲、乙两位同学玩转盘游戏，游戏规则：将圆盘平均分成三份，分别涂上红，黄，绿三种颜色，两位同学分别转动转盘两次（若压线，重新转）．若两次指针指到的颜色相同，则甲获胜；若两次指针指到的颜色是黄绿组合则乙获胜；其余情况则视为平局．
（1）请用画树状图的方法，列出所有可能出现的结果；
（2）试用概率说明游戏是否公平．
25．（9分）综合与实践：
【问题情景】某生物小组探究“酒精对人体的影响”，资料显示，一般饮用低度白酒100毫升后，血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似的用如图所示的图象表示．国家规定，人体血液中的酒精含量大于或等于20（毫克/百毫升）时属于“酒后驾驶”，不能驾车上路．
【实践探究】（1）求部分双曲线BC的函数表达式；
【问题解决】（2）参照上述数学模型，假设某人晚上20：00喝完100毫升低度白酒，则此人第二天早上9：00能否驾车出行？请说明理由．
26．（9分）综合与实践
小明在刘老师的指导下开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．小明继续利用上述结论进行探究．
【提出问题】
如图1，在线段AC同侧有两点B，D，连接AD，AB，BC，CD，如果∠B＝∠D，那么A，B，C，D四点在同一个圆上．
探究展示：
【反思归纳】（1）上述探究过程中的横线上填的内容是 ；
【拓展延伸】（2）如图3，在Rt△ABC中，∠ACB＝90°，AC＝BC，将△ABC绕点A逆时针旋转得△ANM，连接CM交BN于点D，连接BM、AD．小明发现，在旋转过程中，∠CDB永远等于45°，不会发生改变．
①根据∠CDB＝45°，利用四点共圆的思想，试证明ND＝DB；
②在（1）的条件下，当△BDM为直角三角形，且BN＝4时，直接写出BC的长．
2024年广西贵港市中考数学二模试卷
参考答案与试题解析
一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出标号为（A）、（B）、（C）、（D）的四个选项，其中只有一个是正确的．请考生用2B铅笔在答题卡上将选定的答案标号涂黑．
1．（3分）﹣2024的相反数是（ ）
A．2024B．C．﹣2024D．
【分析】根据相反数的定义“只有符号不同的两个数是互为相反数”解答即可．
【解答】解：﹣2024的相反数是2024，
故选：A．
【点评】此题考查了相反数的定义，熟记定义是解题的关键．
2．（3分）据统计，2023年贵港市中考报名人数约为8万，数据8万用科学记数法可表示为（ ）
A．8×105B．0.08×106C．8×104D．0.8×105
【分析】直接根据科学记数法的定义作答即可．
【解答】解：8万＝80000＝8×104，
故选：C．
【点评】本题考查科学记数法，根据科学记数法的表示方法：a×10n，1≤|a|＜10，n为整数，进行表示即可．
3．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
【解答】解：A．该图形既是轴对称图形，也是中心对称图形，故本选项符合题意；
B．该图形是中心对称图形，不是轴对称图形，故本选项不符合题意；
C．该图形是轴对称图形，不是中心对称图形，故本选项不符合题意；
D．该图形既不是轴对称图形，也不是中心对称图形，故本选项不符合题意．
故选：A．
【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．
4．（3分）实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（ ）
A．a＞0B．a＜bC．b﹣1＜0D．ab＞0
【分析】利用数轴与实数的关系，及正负数在数轴上的表示求解．
【解答】解：根据图形可以得到：
﹣2＜a＜0＜1＜b＜3；
所以：A，C，D都是错误的；
故选：B．
【点评】本题考查了数轴与实数的关系，理解并正确运用是解题的关键．
5．（3分）如图是一个正方体积木，它的每个面上都有一个数字，其中1的对面是6，2的对面是5，3的对面是4，现将积木沿着地面标志翻转，最后朝上的面的数字是（ ）
A．4B．3C．2D．5
【分析】根据题意可知，翻转第一次时3朝上；翻转第二次时5朝上．
【解答】解：由题意可知，最后朝上的面的数字是5．
故选：D．
【点评】本题考查正方体的展开图，掌握正方体的展开图是解题的关键．
6．（3分）如图，一束光从点C出发，经过平面镜AE反射后，沿与AB平行的射线DF射出（此时有∠∠1＝∠2），若测得∠3＝100°，则∠A等于（ ）
A．50°B．60°C．70°D．80°
【分析】由平行线的性质可得∠1＝∠2＝∠A，由外角的性质可求解．
【解答】解：∵DF∥AB，
∴∠1＝∠A，
∵∠1＝∠2，
∴∠1＝∠2＝∠A，
∵∠3＝∠A+∠2＝2∠A，∠3＝100°，
∴∠A＝50°，
故选：A．
【点评】本题考查了平行线的性质，掌握平行线的性质是本题的关键．
7．（3分）任意掷一枚骰子，下列情况出现的可能性比较大的是（ ）
A．面朝上的点数是3
B．面朝上的点数是奇数
C．面朝上的点数小于2
D．面朝上的点数不小于3
【分析】分别求出每个事件发生的可能性大小，从而得出答案．
【解答】解：A．面朝上的点数是3的概率为；
B．面朝上的点数是奇数的概率为＝；
C．面朝上的点数小于2的概率为；
D．面朝上的点数不小于3的概率为＝；
∴概率最大的是面朝上的点数不小于3，
故选：D．
【点评】本题主要考查可能性的大小，解题的关键是掌握概率公式．
8．（3分）把多项式m2﹣1分解因式得（ ）
A．（m+1）（m﹣1）B．m（m﹣1）
C．（m+1）2D．（m﹣1）2
【分析】直接利用平方差公式分解因式即可得到答案．
【解答】解：m2﹣1＝（m+1）（m﹣1），
故选：A．
【点评】本题主要考查了分解因式﹣运用公式法，解题的关键是掌握运用公式法分解因式．
9．（3分）“鸡兔同笼”是我国民间流传的诗歌形式的数学题：“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔”解决此问题，设鸡为x只，兔为y只，则所列方程组正确的是（ ）
A．B．
C．D．
【分析】首先明确生活常识：一只鸡有一个头，两只脚；一只兔有一个头，四只脚．
此题中的等量关系为：①鸡的只数+兔的只数＝36只；②2×鸡的只数+4×兔的只数＝100只．
【解答】解：如果设鸡为x只，兔为y只．根据“三十六头笼中露”，得方程x+y＝36；根据“看来脚有100只”，得方程2x+4y＝100．
即可列出方程组．
故选：C．
【点评】根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．本题要用常识判断出隐藏的条件．
10．（3分）如图，AB是圆O的直径，CD是圆O的弦，∠ABD＝69°，则∠C等于（ ）
A．29°B．21°C．31°D．62°
【分析】首先根据同弧所对的圆周角相等求得角A的度数，然后再求得∠ABD的度数即可．
【解答】解：∵AB是直径，
∴∠ADB＝90°，
∵∠ABD＝69°，
∴∠A＝21°，
∴∠C＝21°，
故选：B．
【点评】考查了圆周角定理的知识，解题的关键是熟知圆周角定理的知识，难度不大．
11．（3分）二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1，其中结论正确的为（ ）
A．abc＜0B．b2﹣4ac＝0C．a﹣b+c＞0D．4a+2b+c＜0
【分析】根据所给函数图象，可得出a，b，c的正负，再结合抛物线的对称性及增减性即可解决问题．
【解答】解：由所给函数图象可知，
a＞0，b＜0，c＜0，
所以abc＞0．
故A选项错误．
因为抛物线与x轴有两个不同的交点，
所以方程ax2+bx+c＝0有两个不相等的实数根，
即b2﹣4ac＞0．
故B选项错误．
因为抛物线与x轴的一个交点坐标为（﹣1，0），
所以a﹣b+c＝0．
故C选项错误．
因为抛物线与x轴的一个交点坐标为（﹣1，0），且对称轴为直线x＝1，
所以抛物线与x轴的另一个交点坐标为（3，0）．
又因为抛物线开口向上，
所以当x＝2时，函数值小于零，
即4a+2b+c＜0．
故D选项正确．
故选：D．
【点评】本题考查二次函数的图象和性质，熟知二次函数的图象和性质是解题的关键．
12．（3分）如图，正方形ABCD的边长为4点M是AD的中点，若动点P在对角线AC上，动点Q在CD边上，则PM+PQ的最小值是（ ）
A．4B．C．D．6
【分析】作M关于AC的对称点N，结合正方形性质确定其为AB的中点，当N、P、Q三点共线且NQ⊥CD时，PM+PQ的值最小值．
【解答】解：作M关于AC的对称点N，
又∵四边形ABCD为正方形，
∴点N即为AB的中点，如图：
∴PM+PQ＝PN+PQ≥NQ，
∴当NQ⊥CD时，四边形ANQD为矩形，NQ＝AD＝4，
此时PM+PQ的值最小值为4．
故选：A．
【点评】本题考查的是轴对称的性质和正方形的性质，根据题意作出对称后的图形是解题的关键．
二、填空题：（本大题共6小题，每小题2分，共12分）
13．（2分）如果某天的温度上升了7℃，记作＝7℃，那么温度下降7℃，记作 ﹣7 ℃．
【分析】温度上升用正表示，那么温度下降就用负表示，据此求解即可．
【解答】解：如果某天的温度上升了7℃，记作，那么温度下降7℃，记作﹣7℃，
故答案为：﹣7．
【点评】本题主要考查了正负数的实际应用，在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
14．（2分）若代数式有意义，则实数x的取值范围是 x≠2 ．
【分析】根据分式的分母不为零列出不等式，解不等式得到答案．
【解答】解：由题意得：x﹣2≠0，
解得：x≠2，
故答案为：x≠2．
【点评】本题考查的是分式有意义的条件，熟记分式的分母不为零是解题的关键．
15．（2分）某校九年级有8个班级，人数分别为37，a，32，36，37，32，38，34．若这组数据的众数为32，则这组数据的中位数为 35 ．
【分析】根据众数、中位数的定义分别进行解答，即可求出答案．
【解答】解：∵一组数据37，a，32，36，37，32，38，34的众数为32，
∴a＝32，
把这组数据从小到大排列为32，32，32，34，36，37，37，38，排在中间的两个数分别为34，36，所以这组数据的中位数为＝35．
故答案为：35．
【点评】本题考查了确定一组数据的中位数和众数的能力．要明确定义，一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．
16．（2分）如图，有一斜坡AB，此斜坡的坡面长AB＝40m，斜坡的坡角是∠BAC，若，则坡顶B离地面的高度BC为 16 m．
【分析】由正弦三角函数定义即可得出答案．
【解答】解：∵，
∴，
故答案为：16．
【点评】本题考查了正弦三角函数，熟练掌握正弦三角函数为角的对边比邻边是解题的关键．
17．（2分）如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，AB＝12，则圆环的面积为 36π ．
【分析】设AB与小圆的切点为C，连接OC、OA，由勾股定理可求得OA2﹣OC2＝AC2，再结合圆的面积可求得阴影部分的面积．
【解答】解：如图，设AB与小圆的切点为C，连接OC、OA，
∵AB为小圆的切线，
∴OC⊥AB，
∴AC＝AB＝6，
由勾股定理可得AO2﹣OC2＝AC2＝36，
∴S圆环＝S大圆﹣S小圆＝πOA2﹣πOC2＝π（OA2﹣OC2）＝πAC2＝36π，
故答案为：36π．
【点评】本题主要考查切线的性质，掌握连接圆心和切点的半径与切线垂直是解题的关键，注意整体思想的应用．
18．（2分）以△ABC的顶点A为圆心，大于二分之一AC为半径画弧与AC，AB分别交于两点，分别以这两点为圆心，以大于二分之一两点间距离为半径（半径不变）画弧．已知∠C＝90°，∠B＝30°，AB＝4，那么CD的长为 ．
【分析】根据角平分线的作图可得∠CAD＝30°，利用勾股定理和30°角的直角三角形的性质求出DC的长即可．
【解答】解：在Rt△ACB中，∠B＝30°，AB＝4，
∴AC＝2，∠BAC＝60°，
∴，
∴在Rt△ACD中，AD＝2CD，
∴AC2+CD2＝4CD2，
∴3CD2＝22，
∴，
故答案为：．
【点评】本题考查的是角平分线的作图，勾股定理，熟练掌握含30度角的直角三角形特征是关键．
三、解答题（本大题共8小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
19．（9分）计算：．
【分析】先算乘法、乘方，再算除法，最后算加减即可．
【解答】解：原式＝﹣2+4÷4
＝﹣2+1
＝﹣1．
【点评】本题考查了含乘方得有理数的混合运算，熟练掌握其运算法则是解题的关键．
20．（9分）解方程组：．
【分析】方程组利用加减消元法求出解即可．
【解答】解：解方程组：，
①+②，得3x＝9，
解得 x＝3，
将x＝3代入方程②，得3﹣y＝2，
解得 x＝1，
所以原方程组的解是．
【点评】本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
21．（9分）如图，已知AE∥BF，AC平分∠BAE．
（1）尺规作图：作∠ABF的平分线交AC于点O，交AE于点D；
（要求：保留作图痕迹，不写作法，标明字母）
（2）求证：△ABO≌△ADO．
【分析】（1）根据角平分线的作法即可完成作图；
（2）先证明∠AOB＝∠AOD＝90°，然后利用ASA即可证明△ABO≌△ADO．
【解答】（1）解：如图所示，即为所求；
（2）证明：∵AE∥BF，
∴∠ABC+∠BAD＝180°，
∵AC平分∠BAE，BD平分∠ABF，
∴∠BAC＝BAD，∠ABD＝ABC，
∴∠BAC+∠ABD＝（∠BAD+∠ABC）＝90°，
∴∠AOB＝∠AOD＝90°，
在△ABO和△ADO中，
，
∴△ABO≌△ADO（ASA）．
【点评】本题考查了作图﹣基本作图，全等三角形的判定，角平分线定义，解决本题的关键是掌握基本作图方法．
22．（9分）某学校为了美化校园环境，打造绿色校园，计划用长为120米的篱笆来围成一个一面靠墙（墙足够长）的矩形花园，并用一道篱笆把花园分为A和B两块区域（如图所示）．（1）设垂直于墙的一边长为x米，则平行于墙的一边长为 （120﹣3x） 米；
（2）请设计一个方案，使得花园的面积最大，并求出最大面积．
（3）在花园面积最大的条件下，A和B两块区域分别种植牡丹和芍药，每平方米种植2株，已知牡丹每株的售价为25元，芍药每株的售价为15元，学校计划购买这些植物的费用不超过5万元，求学校最多能购买多少株牡丹．
【分析】（1）直接根据图形列出代数式即可；
（2）设围成的矩形面积为S平方米，再结合（1）可得到S与x的函数关系式，再配成顶点式求出函数的最大值即可；
（3）设购买牡丹m株，则购买芍药1200×2﹣m＝（2400﹣m）株，再根据题意列出不等式即可求得种植牡丹面积的最大值．
【解答】解：（1）设垂直于墙的一边长为x米，则平行于墙的一边长为120﹣3x．
故答案为：（120﹣3x）；
（2）设围成的矩形面积为S平方米，根据（1）得：
S＝x（120﹣3x）＝﹣3x2+120x＝﹣3（x﹣20）2+1200，
∵﹣3＜0，
∴当x＝20时，S取最大值1200，
∴当垂直于墙的一边长为20米时，花园面积最大为1200平方米；
（3）设购买牡丹m株，则购买芍药1200×2﹣m＝（2400﹣m）株，
∵学校计划购买费用不超过5万元，25m+15（2400﹣m）≤50000，
解得m≤1400，
∴最多可以购买1400株牡丹．
【点评】本题主要考查了二次函数的应用、一元一次不等式的应用等知识点，明确题意、找出所求问题需要的条件是解题的关键．
23．（9分）如图，点A，C均在⊙O上，OA⊥OC，⊙O外一点P在直线OC上，连接PA交⊙O于点B，作点B关于PC的对称点D，以点D为顶点作∠ADE＝∠PAO，点E在PA上．
（1）求证：ED是⊙O的切线；
（2）若AD平分∠PAO，，求DE的长．
【分析】（1）连接OD，OB，根据对称的性质可得点D必在⊙O上，OD是⊙O的半径，，根据圆周角定理有，从而∠POD＝∠PAD，进而得到∠ADO＝∠APO，由O A⊥P C得到∠PAO+∠APO＝90°，因此∠ADE+∠ADO＝90°，即ED⊥OD，得证结论；
（2）先求得∠APO＝∠PAD＝∠DAO＝30°，进而∠PAO＝∠AOD+∠PAD＝60°，∠AED＝90°，因此，根据OA＝OB，∠PAO＝60°，得到△OAB是等边三角形，根据三线合一得到AD⊥OB，，而在Rt△AOF中，从而．
【解答】（1）证明：如图，连接OD，OB，记OP与AD的交点为G，
∵点B在⊙O上，PC是经过圆心O的直线，
∴点B关于PC的对称点D必在⊙O上，
∴OD是⊙O的半径，
∵点A在⊙O上，
∴，
∵点B和点D关于PD对称，
∴，
∴∠POD＝∠PAD，
∵∠ADO＝180°﹣∠DGO﹣∠POD，∠APO＝∠180°﹣∠AGP﹣∠PAD，
又∠DGO＝∠AGP，
∴∠ADO＝∠APO，
∵O A⊥P C于点O，
∴∠AOP＝90°，
∴∠PAO+∠APO＝90°，
又∠ADE＝∠PAO，
∴∠ADE+∠ADO＝90°，即ED⊥OD，
∴ED是⊙O的切线；
（2）解：记OB与AD的交点为F，
∵AD平分∠PAO，
∴∠DAO＝∠PAD，
∵OA＝OD，
∴∠DAO＝∠ADO，
∵∠APO＝∠ADO，∠PAO+∠APO＝90°，
∴∠APO＝∠PAD＝∠DAO＝30°，∠PAO＝∠AOD+∠PAD＝60°
又∠ADE＝∠PAO＝60°，
∴∠AED＝90°，
∴在Rt△ADE中得：，
∵OA＝OB，∠PAO＝60°，
∴△OAB是等边三角形，
∴AD⊥OB
∵OA＝OD，
∴，
在Rt△AOF中得：，
∴．
【点评】本题主要考查圆周角定理，等边三角形的判定，等腰三角形的性质，切线的证明，轴对称的性质，综合运用相关知识是解题的关键．
24．（9分）甲、乙两位同学玩转盘游戏，游戏规则：将圆盘平均分成三份，分别涂上红，黄，绿三种颜色，两位同学分别转动转盘两次（若压线，重新转）．若两次指针指到的颜色相同，则甲获胜；若两次指针指到的颜色是黄绿组合则乙获胜；其余情况则视为平局．
（1）请用画树状图的方法，列出所有可能出现的结果；
（2）试用概率说明游戏是否公平．
【分析】（1）画出树状图，进一步一一列举得出所有情况即可；
（2）计算甲、乙获胜的概率，进一步比较得出答案即可．
【解答】解：（1）如图所示：
（红，红），（红，黄），（红，绿），（黄，红），（黄，黄），
（黄，绿），（绿，红），（绿，黄），（绿，绿） 共9种情况；
（2）P（甲获胜）＝＝，
P（乙获胜）＝，
P（甲获胜）＞P（乙获胜），
所以游戏不公平．
【点评】本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平．利用概率＝所求情况数与总情况数之比解决问题．
25．（9分）综合与实践：
【问题情景】某生物小组探究“酒精对人体的影响”，资料显示，一般饮用低度白酒100毫升后，血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似的用如图所示的图象表示．国家规定，人体血液中的酒精含量大于或等于20（毫克/百毫升）时属于“酒后驾驶”，不能驾车上路．
【实践探究】（1）求部分双曲线BC的函数表达式；
【问题解决】（2）参照上述数学模型，假设某人晚上20：00喝完100毫升低度白酒，则此人第二天早上9：00能否驾车出行？请说明理由．
【分析】（1）由待定系数法可以求出OA的函数表达式，从而得到A点坐标，进一步得到B点坐标，然后再利用待定系数法可以得到部分双曲线BC的函数表达式；
（2）在部分双曲线BC的函数表达式中令y＜20，可以得到饮用低度白酒100毫升后完全醒酒的时间范围，再把题中某人喝酒后到准备驾车的时间间隔进行比较即可得解．
【解答】解：（1）设OA的函数表达式为y＝kx，则：
，
∴k＝60，
∴OA的函数表达式为y＝60x，
∴当x＝时，y＝90，
可设部分双曲线BC的函数表达式为y＝，
由图象可知，当x＝3时，y＝90，
∴m＝270，
∴部分双曲线BC的函数表达式为y＝；
（2）在y＝中，令y＜20，
可得：，
解之可得：x＞13.5，
∵晚上20：00到第二天早上9：00的时间间隔为9+4＝13（h），13h＜13.5h，
∴某人晚上20：00喝完100毫升低度白酒，则此人第二天早上9：00时体内的酒精含量高于20（毫克/百毫升），
∴某人晚上20：00喝完100毫升低度白酒，则此人第二天早上9：00不能驾车出行．
【点评】本题考查反比例函数的应用，熟练掌握一次函数与反比例函数的图象、待定系数法的应用是解题关键．
26．（9分）综合与实践
小明在刘老师的指导下开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．小明继续利用上述结论进行探究．
【提出问题】
如图1，在线段AC同侧有两点B，D，连接AD，AB，BC，CD，如果∠B＝∠D，那么A，B，C，D四点在同一个圆上．
探究展示：
【反思归纳】（1）上述探究过程中的横线上填的内容是 ∠AEC+∠B＝180° ；
【拓展延伸】（2）如图3，在Rt△ABC中，∠ACB＝90°，AC＝BC，将△ABC绕点A逆时针旋转得△ANM，连接CM交BN于点D，连接BM、AD．小明发现，在旋转过程中，∠CDB永远等于45°，不会发生改变．
①根据∠CDB＝45°，利用四点共圆的思想，试证明ND＝DB；
②在（1）的条件下，当△BDM为直角三角形，且BN＝4时，直接写出BC的长．
【分析】（1）根据已给推论过程证明即可；
（2）①根据旋转的性质，证明∠MDB＝45°；
②分当∠BMD＝90°时，当∠DBM＝90°时，根据四点共圆、圆周角定理证明△ABN和△ACM相似，得到相应线段的长，再利用勾股定理即可求解．
【解答】（1）解：如图2，作经过点A，C，D的⊙O，在劣弧AC上取一点E（不与A，C重合），连接AE，CE，
则∠AEC+∠D＝180°，
又∵∠B＝∠D，
∴∠AEC+∠B＝180°，
∴点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆），
∴点B，D在点A，C，E所确定的⊙O上，
∴点A，B，C，D四点在同一个圆上，
故答案为：∠AEC+∠B＝180°；
（2）①证明：∵在Rt△ACB中，AC＝BC，如图3，
∴∠BAC＝45°，
∵∠CDB＝45°，
∴∠CDB＝∠BAC＝45°，
∴A，C，B，D四点共圆，
∴∠ADB+∠ACB＝180°，
∵∠ACB＝90°，
∴∠ADB＝90°，
∴AD⊥BN，
∵△ACB旋转得△AMN，
∴△ACB≌△AMN，
∴AB＝AN，
∵AD⊥BN，
∴ND＝DB；
②如图4，当∠BMD＝90°时，
∵CA＝CB，∠ACB＝90°，
∴，
∵，∠NAB＝MAC，
∴△NAB∽△MAC，
∴，
∵BN＝4，
∴，
又∵∠CDB＝45°，∠DMB＝90°，，
∴，
∴；
如图5，当∠DBM＝90°时，
过B作BH⊥CD交CD于H，
∵CA＝CB，∠ACB＝90°，
∴，
∵，∠NAB＝MAC，
∴△NAB∽△MAC，
∴，
∵BN＝4，
∴，
∵∠CDB＝45°，∠NBM＝90°，
∴，
∵BH⊥CD，
∴，
∴，
∴．
【点评】本题考查了直角所对的弦是直径，圆内接四边形对角互补，确定圆的条件，相似三角形的性质与判定，勾股定理，等腰三角形的性质与判定，熟练掌握以上知识是解题的关键．
如图2，作经过点A，C，D的⊙O，在劣弧AC上取一点E（不与A，C重合），连接AE，CE，
则∠AEC+∠D＝180°
又∵∠B＝∠D，
∴ ，
∴点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆），
∴点B，D在点A，C，E所确定的⊙O上
∴点A，B，C，D四点在同一个圆上．
如图2，作经过点A，C，D的⊙O，在劣弧AC上取一点E（不与A，C重合），连接AE，CE，
则∠AEC+∠D＝180°
又∵∠B＝∠D，
∴ ∠AEC+∠B＝180° ，
∴点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆），
∴点B，D在点A，C，E所确定的⊙O上
∴点A，B，C，D四点在同一个圆上．