





高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制授课课件ppt
展开奥运会赛场上,跳水运动员的优美动作引来阵阵喝彩.跳水(Diving)是一项优美的水上运动,它是从高处通过空中转体,并以特定动作入水的运动.
问题 如果跳水运动员在空中顺时针连续转体一周半,那么运动员转过的角度是多少?
知识点一 任意角的概念
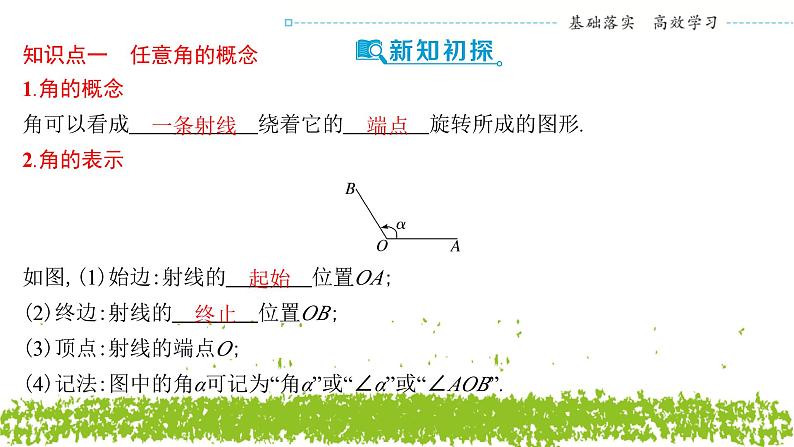
角可以看成 一条射线 绕着它的 端点 旋转所成的图形.
如图,(1)始边:射线的 起始 位置OA;
(2)终边:射线的 终止 位置OB;
(3)顶点:射线的端点O;
(4)记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
1.始边与终边重合的角一定是零角吗?
提示:不一定.只有始边没有做任何旋转,始边与终边重合的角才是零角.
2.正角、负角、零角是根据什么区分的?
提示:根据组成角的射线是否旋转及旋转方向.
知识点二 角的加、减法设α,β是任意两个角:(1)角的加法:把角α的终边旋转角β,这时终边所对应的角是 α+β .α+β角的始边为α的始边,终边为β的终边;(2)相反角:把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为 相反角 ,角α的相反角记为 -α ;(3)角的减法:像实数减法的“减去一个数等于加上这个数的相反数”一样,我们有α-β=α+(-β).这样,角的减法可以转化为角的加法.
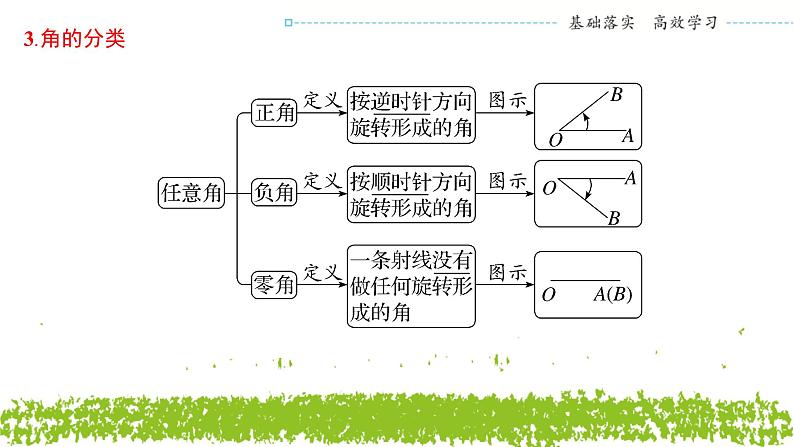
知识点三 象限角与终边相同的角1.象限角:在平面直角坐标系中,若角的顶点与 原点 重合,角的始边与 x 轴的非负半轴重合,那么,角的 终边 在第几象限,就说这个角是第几 象限角 ;如果角的终边在 坐标轴上 ,那么就认为这个角不属于任何一个象限.2.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S= {β|β=α+k·360°,k∈Z} ,即任一与角α终边相同的角,都可以表示成角α与 整数个周角 的和.提醒 对集合S={β|β=α+k·360°,k∈Z}的理解:①角α为任意角,“k∈Z”不能省略;②k·360°与α中间要用“+”连接,k·360°-α可理解成k·360°+(-α);③相等的角的终边一定相同,而终边相同的角不一定相等;终边相同的角有无数个,它们相差360°的整数倍.
{β|β=α+k·360°,k∈Z}
1.若手表时针走过4小时,则时针转过的角度为( )
2.设α=-300°,则与α终边相同的角的集合为( )
解析:B 因为α=-300°=-360°+60°,所以角α的终边与60°角的终边相同,故选B.
3.角α=-60°+k·180°(k∈Z)的终边落在( )
解析:D 令k=0,则α=-60°,角α的终边在第四象限;再令k=1,则α=-60°+180°=120°,角α的终边在第二象限,故选D.
【例1】 (多选)下列说法正确的是( )
解析 锐角是大于0°且小于90°的角,终边落在第一象限,是第一象限角,所以A正确;-350°角是第一象限角,但它是负角,所以B错误;0°角是小于180°的角,但它既不是钝角,也不是直角或锐角,所以C错误;由于在90°≤β<180°范围内的角β包含90°角,所以不一定是钝角,所以D正确.
通性通法理解与角的概念有关问题的关键关键在于正确理解象限角与锐角、直角、钝角、平角、周角等概念,弄清角的始边与终边及旋转方向与大小.另外需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需要举一个反例即可.
1.射线OA绕端点O逆时针旋转120°到达OB位置,由OB位置顺时针旋转270°到达OC位置,则∠AOC=( )
解析:B 各角和的旋转量等于各角旋转量的和.所以∠AOC=120°+(-270°)=-150°,故选B.
2.经过2个小时,钟表的时针和分针转过的角度分别是( )
【例2】 已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角:
(1)最小的正角为315°.
解 因为-1 845°=-45°+(-5)×360°,即-1 845°角与-45°角的终边相同,所以与角α终边相同的角的集合是{β|β=-45°+k·360°,k∈Z}.
解 (2)最大的负角为-45°.
(3)-360°~720°范围内的角.
解 (3)-360°~720°范围内的角分别是-45°,315°,675°.
通性通法终边相同的角的表示(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式;(2)终边相同的角相差360°的整数倍;(3)终边在同一直线上的角之间相差180°的整数倍.
1.若角2α与240°角的终边相同,则α=( )
解析:B 角2α与240°角的终边相同,则2α=240°+k·360°,k∈Z,则α=120°+k·180°,k∈Z.
2.写出与75°角终边相同的角的集合,并求在360°~1 080°范围内与75°角终边相同的角.
解:与75°角终边相同的角的集合为S={β|β=k·360°+75°,k∈Z}.当360°≤β≤1 080°,即360°≤k·360°+75°≤1 080°时,
【例3】 (1)(多选)在①160°;②480°;③-960°;④1 530°这四个角中,是第二象限角的是( )
解析 (1)第二象限角α需满足k·360°+90°<α<k·360°+180°,k∈Z,分析可知:①是第二象限角;②是第二象限角;③是第二象限角;④不是第二象限角.故选A、B、C.
(变设问)在本例(2)的条件下,求角2α的终边的位置.
解:∵α是第二象限角,∴k·360°+90°<α<k·360°+180°(k∈Z).∴k·720°+180°<2α<k·720°+360°(k∈Z).∴角2α的终边在第三或第四象限或在y轴的非正半轴上.
1.-1 060°的终边落在( )
解析:A 因为-1 060°=-3×360°+20°,所以-1 060°的终边落在第一象限.
【例4】 已知角α的终边在图中阴影部分内,试指出角α的取值范围.
解 终边在30°角的终边所在直线上的角的集合为S1={α|α=30°+k·180°,k∈Z},终边在180°-75°=105°角的终边所在直线上的角的集合为S2={α|α=105°+k·180°,k∈Z},因此,终边在图中阴影部分内的角α的取值范围为{α|30°+k·180°≤α<105°+k·180°,k∈Z}.
通性通法1.求解终边在某条直(射)线上的角的集合的思路(1)若所求角β的终边在某条直线上,则集合的形式为{β|β=k·180°+α,k∈Z};(2)若所求角β的终边在某条射线上,则集合的形式为{β|β=k·360°+α,k∈Z}.2.表示区域角的三个步骤第一步:先按逆时针的方向找到区域的起始和终止边界;第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α<x<β},其中β-α<360°;第三步:起始、终止边界对应角α,β再加上360°的整数倍,即得区域角集合.
(1)分别写出终边落在OA,OB位置上的角的集合;
解 (1)终边落在OA位置上的角的集合为{α|α=210°+k·360°,k∈Z},终边落在OB位置上的角的集合为{α|α=300°+k·360°,k∈Z}.
(2)写出终边落在阴影部分(包括边界)的角的集合.
解 (2)终边落在阴影部分(包括边界)的角的集合是{α|210°+k·360°≤α≤300°+k·360°,k∈Z}.
4.终边相同的角和角的终边相同
1.把一条射线绕着端点按顺时针方向旋转240°所形成的角是( )
解析:D 一条射线绕着端点按顺时针方向旋转240°所形成的角是-240°,故选D.
2.-495°角的终边与下列哪个角的终边相同( )
解析:C 因为-495°=-2×360°+225°,所以与-495°角终边相同的是225°角.故选C.
3.已知角α在平面直角坐标系中如图所示,其中射线OA与y轴正半轴的夹角为30°,则α=( )
解析:D 由角α按逆时针方向旋转,可知α为正角.又旋转量为480°,∴α=480°.
4.在0°~360°范围内,找出与下列各角终边相同的角,并指出它们分别是第几象限角:
(1)-150°;(2)650°.
解:(1)因为-150°=-360°+210°,所以在0°~360°范围内,与-150°角终边相同的角是210°角,它是第三象限角.
(2)因为650°=360°+290°,所以在0°~360°范围内,与650°角终边相同的角是290°角,它是第四象限角.
高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制背景图ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000280_t3/?tag_id=26" target="_blank">5.1 任意角和弧度制背景图ppt课件</a>,共44页。
人教A版 (2019)必修 第一册5.1 任意角和弧度制课堂教学课件ppt: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000280_t3/?tag_id=26" target="_blank">5.1 任意角和弧度制课堂教学课件ppt</a>,共24页。PPT课件主要包含了角的分类,逆时针,顺时针,知识点2象限角等内容,欢迎下载使用。
人教A版 (2019)必修 第一册5.1 任意角和弧度制评课ppt课件: 这是一份人教A版 (2019)必修 第一册5.1 任意角和弧度制评课ppt课件,共49页。PPT课件主要包含了必备知识·自主学习,逆时针,顺时针,非负半轴,第几象限角,关键能力·合作学习,课堂检测·素养达标等内容,欢迎下载使用。













