湖南省永州市冷水滩区京华中学2024年中考模拟数学试题(含答案)

展开

这是一份湖南省永州市冷水滩区京华中学2024年中考模拟数学试题(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的；请将你认为正确的选项填涂到答题卡上）
1．熊大比熊二大2岁，如果熊二y岁，则熊大（）
A．岁B．岁C．岁D．岁
2．剪纸是一种传统的民间艺术，有着悠久的历史传承．下列剪纸作品为中心对称图形的是（）
A．B．C．D．
3．“霜降见霜，谷米满仓”，2023年我国粮食再获丰收．据统计，去年秋粮的种植面积为13.1亿亩，比前年增加了700多万亩，奠定了增产的基础．将1310000000用科学记数法表示应为（）
A．B．C．D．
4．已知一组数据26，36，36，2■，41，42，其中一个两位数的个位数字被墨水涂污，则关于这组数据下列统计量的计算结果与被涂污数字无关的是（）
A．平均数B．方差C．中位数D．众数
5．神奇的自然界处处隐含着数学美！生物学家在向日葵圆盘中发现：向日葵籽粒成螺线状排列，螺线的发散角是137.5°．我们知道圆盘一周为360°，，．这体现了（）
A．轴对称B．旋转C．平移D．黄金分割
6．由6个同样的立方体摆出从正面看是的几何体，下面摆法正确的是（）
A．B．C．D．
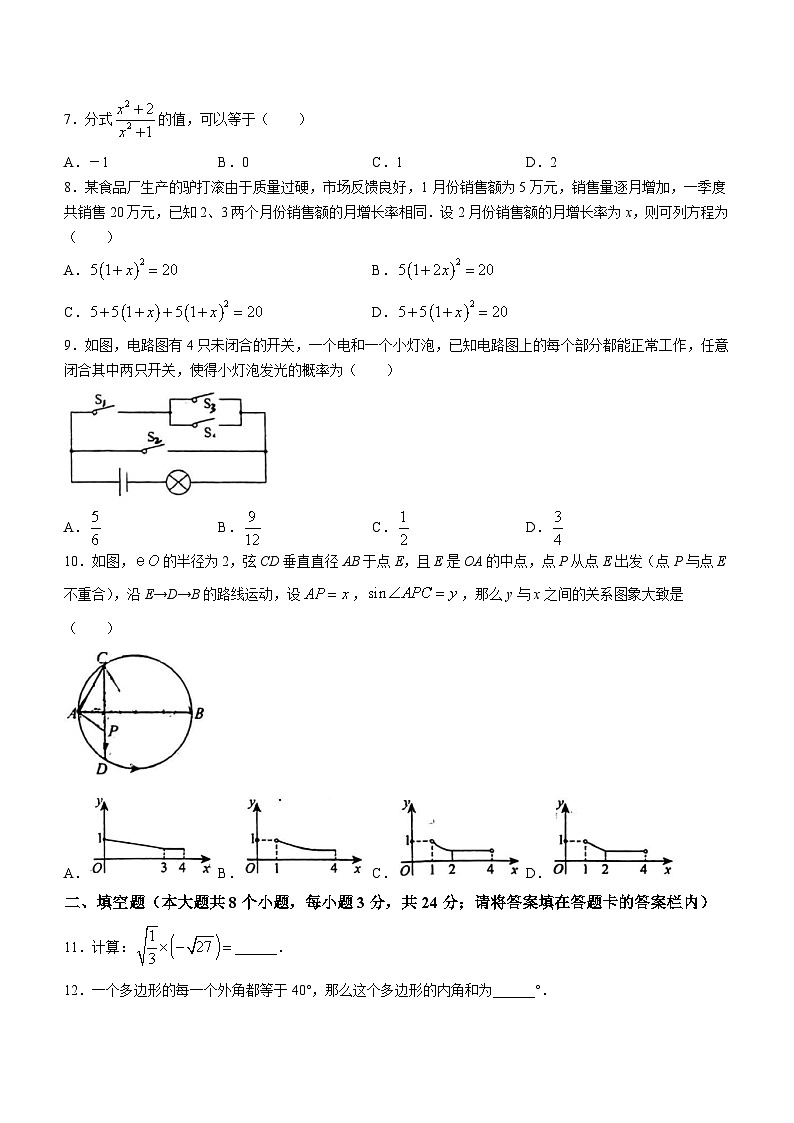
7．分式的值，可以等于（）
A．－1B．0C．1D．2
8．某食品厂生产的驴打滚由于质量过硬，市场反馈良好，1月份销售额为5万元，销售量逐月增加，一季度共销售20万元，已知2、3两个月份销售额的月增长率相同．设2月份销售额的月增长率为x，则可列方程为（）
A．B．
C．D．
9．如图，电路图有4只未闭合的开关，一个电和一个小灯泡，已知电路图上的每个部分都能正常工作，任意闭合其中两只开关，使得小灯泡发光的概率为（）
A．B．C．D．
10．如图，的半径为2，弦CD垂直直径AB于点E，且E是OA的中点，点P从点E出发（点P与点E不重合），沿E→D→B的路线运动，设，，那么y与x之间的关系图象大致是（）
A．B．C．D．
二、填空题（本大题共8个小题，每小题3分，共24分；请将答案填在答题卡的答案栏内）
11．计算：______．
12．一个多边形的每一个外角都等于40°，那么这个多边形的内角和为______°．
13．已知反比例函数经过点，则k的值是______．
14．如图，在中，．过点C作的平分线交AB于点D，过点A作，交BC延长线于点E．若，则______°．
15．已知菱形ABCD的对角线AC、BD的长度是关于x的方程的两个实数根，则此菱形的面积是______．
16．明代数学家程大位编撰的《算法统宗》记载了“绳索量竿”问题：“一条竿子一条索，索比竿子长一托，折回索子来量竿，却比竿子短一托．”译文为：“有一根竿和一条绳，若用绳去量竿，则绳比竿长5尺；若将绳对折后再去量竿，则绳比竿短5尺，那么绳索长______尺．（注：“托”和“尺”为古代的长度单位，1托＝5尺）
17．为了给同学庆祝生日，小明自己动手用扇形纸片制作了一顶圆锥形生日帽，生日帽的底面圆半径r为7cm，高h为24cm，则该扇形纸片的面积为______．
18．如图：中，，，，把边长分别为，，，…的n个正方形依次放在中；第一个正方形的顶点分别放在的各边上；第二个正方形的顶点分别放在的各边上，其他正方形依次放入，则第2024个正方形的边长为______．
三、解答题（本大题共8个小题，共66分，解答题要求写出证明步骤或解答过程）
19．（6分）计算：．
20．（6分）解不等式，并求它的非正整数解．
21．（8分）如图，在平行四边形ABCD中，对角线BD，AC相交于点O，，，垂足分别为E，F．若，求证：四边形ABCD为矩形．
22．（8分）为提高居民防范电信网络诈骗的意识，某社区举办相关知识比赛．现从该社区甲、乙两个参赛代表队中各随机抽取10名队员的比赛成绩，并进行整理、描述和分析（分数用x表示，共分为四组：A．，B．，C．，D．）．
下面给出了部分信息：
甲队10名队员的比赛成绩：69，79，88，90，92，94，94，96，98，100．
乙队10名队员的比赛成绩在D组中的所有数据为：92，92，97，99，99，99．
甲、乙代表队中抽取的队员比赛成绩统计表
根据以上信息，解答下列问题：
（1）填空：______，______，______；
（2）该社区甲代表队有200名队员、乙代表队有230名队员参加了此次比赛，估计此次比赛成绩在A组的队员共有多少名；
（3）根据以上数据，你认为甲、乙哪个代表队的比赛成绩更好？请说明理由（写出一条理由即可）．
23．（9分）如图某货船以20海里/h的速度将一批重要的物资由A处运往正西方向的B处，经16h的航行到达，到达后必须立即卸货．此时，接到气象部门的通知，一台风中心、以40海里/h的速度由A处向北偏西60°方向移动，距台风中心200海里以内的圆形区域会受到影响．（）问：
（1）B处是否会受到台风的影响？请说明理由．
（2）如果B处受到台风影响，那么求出影响的时间．
24．（9分）如图，一农户要建一个矩形鸡舍，为了节省材料，鸡舍的一边利用长为a米的墙，另外三边用长为31米的建筑材料围成，为方便进出，在垂直墙的一边留下一个宽1米的门．设米时，鸡舍面积为S平方米．
（1）求S关于x的函数表达式及x的取值范围．
（2）在（1）的条件下，当AB为多少时，鸡舍的面积为96平方米？
（3）若住房墙的长度足够长，问鸡舍面积能否达到130平方米？
25．（10分）在中，，AO平分交BC于点O，以OC为半径作．
（1）求证：直线AB是的切线．
（2）若，，求的半径．
26．（10分）如图①，已知抛物线与x轴交于，两点，与y轴交于点C．
（1）求该抛物线的表达式；
（2）若点D是抛物线上第一象限内的一个动点，连接CD，BD，BC，AC．当的面积等于面积的2倍时，求点D的坐标；
（3）抛物线上是否存在点P，使得？若存在，请求出点P的坐标；若不存在，请说明理由．
2024年中考数学仿真试题（二）
参考答案
一、选择题
1--5 BDBCD 6-10 BDCAC
二、填空题
11．-3 12．1260 13．-5 14．72． 15．27
16．20 17．175π 18．（
三、解答题
19．（6分）
解：=0
20．（6分）
移项，得，
合并同类项，得，
不等式的两边同时除以2，得，
所以，原不等式的解集为．··························3分
如图所示：
所以非负整数解是-4、-3、-2、-1、0··········6分
21．（8分）
证明：∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∵AE⊥BD，BF⊥AC，
在Rt△ADE与Rt△BCF中，
，
∴Rt△ADE≌Rt△BCF（HL），····················3分
∴∠ADE＝∠BCF＝∠DAO
∴DO＝AO，······································6分
由平行边形的性质可得，AC＝BD，
∴平行四边形ABCD是矩形．·······················8分
22．（8分）
解：（1）
a=93，b=99，m=10；·····························3分
（2）20023043（名），
估计此次比赛成绩在A组的队员共有43名；·········6分
（3）乙队成绩好．·······························7分
因为乙对的众数远远高于甲队．····················8分
23．（9分）
（1）解：如图1，过点B作交于点D，
∵在中，
∴,····················1分
∵海里
∴海里··········3分
∵，
∴会受台风影响．······················4分
（2）如图2，
如图，海里，
在中，
海里，···············6分
同时在点D右侧相同的距离内点B也受影响，
∴小时，
∴影响的时间为小时．································9分
24．（9分）
解：设AB=2x米时，则BC=（31+1-2x）米，·············1分
鸡舍面积为S平方米，
根据题意得，S=（31+1-2x）x=-2+32x=-2+128；···········2分
∵31+1-2x>0，≥0
∴x<16，x≥8
∴x的取值范围为8≤x<16．········································3分
解：根据题意得：-2+32x=96，解得=12，·············5分
∵x的取值范围为8≤x<16
∴x=12．
答：当为12米时，鸡舍的面积为96平方米．····················6分
解：根据题意得-2+32x=130：，整理得，-16x+65=0，∆=-4×65<0，
所以方程没有实数根，················································8分
∴鸡舍面积不能达到130平方米．······································9分
25．（10分）
（1）证明：过作于，
，
平分，
，
，
（），·············································3分
，
与相切；····················································5分
（2）解：，
设
则
，，
，·····················································6分
，
，
，
在中，，
即：，···········································7分
解得或（舍去），
的半径为．··················································10分
26．（10）
（1）解：把代入中，得：
，解得：，·························2分
∴抛物线解析式为；·························3分
（2）解：过点作轴平行线交轴于，交于点，作于点，
把代入中，得：，
∴点坐标是，·····································4分
设直线，
把，，代入，得
，
解得，·∴直线的解析式为
设，则，
∴
由得：，
∴
整理得：
解得：
∵，
∴的值为或，················································5分
当时，，
当时，，
∴点的坐标为或；·······································6分
（3）解：存在．···················································7分
由，，，得，
∴，
①当点在左侧时．
在轴上取点，，延长交抛物线于点．
在和中
，
∴，∴，
∴，
设直线的解析式为，
将代入，得
，解得，
∴设直线的解析式为，
由得：或，
∴；·················································8分
②当点在右侧时，
作关于的对称，交二次函数于点，则，，
∴，
∵，
∴四边形是正方形，
∴，
令中，，则，
解得或，
∴······················································9分
，
∵，,
∴，∴，
∴
∴点在抛物线上，即点满足条件．
故存在满足条件的点有两个，分别是，，，．················10分
代表队
平均数
中位数
众数
“C”组所占百分比
甲
90
a
94
10%
乙
90
92
b
20%