2024海南中考数学二轮专题训练 几何图形动点型综合题 (含答案)

这是一份2024海南中考数学二轮专题训练 几何图形动点型综合题 (含答案)，共20页。试卷主要包含了5°等内容，欢迎下载使用。
模型再现：自旋转型全等模型
1. 如图，在矩形ABCD中，点E是BC上一动点，连接DE，点F是DE上一点，DF＝CE，BC＝DE.求证：AF⊥DE.
【思维教练】由矩形ABCD的性质可知∠ADF＝∠DEC，由BC＝DE，得AD＝DE，再由已知条件DF＝CE，即可证得△ADF≌△DEC，可得∠AFD＝∠C＝90°，即可得证．
第1题图
模型再现：一线三垂直型相似模型
2. 如图，在矩形ABCD中，AB＝4，BC＝5，E是BC边上的一个动点，DF⊥AE，垂足为点F，若AE＝BC，求tan ∠FCE的值．
【思维教练】要求tan ∠FCE的值，先过点F作BC的垂线，构造直角三角形，再结合矩形的性质和相似三角形的性质列出比例关系，即可求解．
第2题图
模型再现：8字型相似模型
3. 如图，在矩形ABCD中，E是BC边上一动点，AE⊥BD，垂足为点F，连接DE.若BE＝ eq \f(1,2) BC，求cs ∠AED的值．
【思维教练】要求cs ∠AED的值，即要求Rt△EFD中 eq \f(EF,ED) 的值，结合矩形的性质和相似三角形的性质即可得出EF＝ eq \f(1,3) AE＝ eq \f(1,3) DE.
第3题图
模型再现：正A字型相似模型
4. 如图，在矩形ABCD中，AB＝3，BC＝5，E是AD上一个动点，连接BD，O是对角线BD的中点，连接OE，AO，当OE＝DE时，求AE的长．
【思维教练】由矩形ABCD的性质和勾股定理，可得BD的长，再通过角度之间的等量关系转换，得△ODE∽△ADO，结合相似的性质对应边成比例得出AE的长．
第4题图
(对接中考)
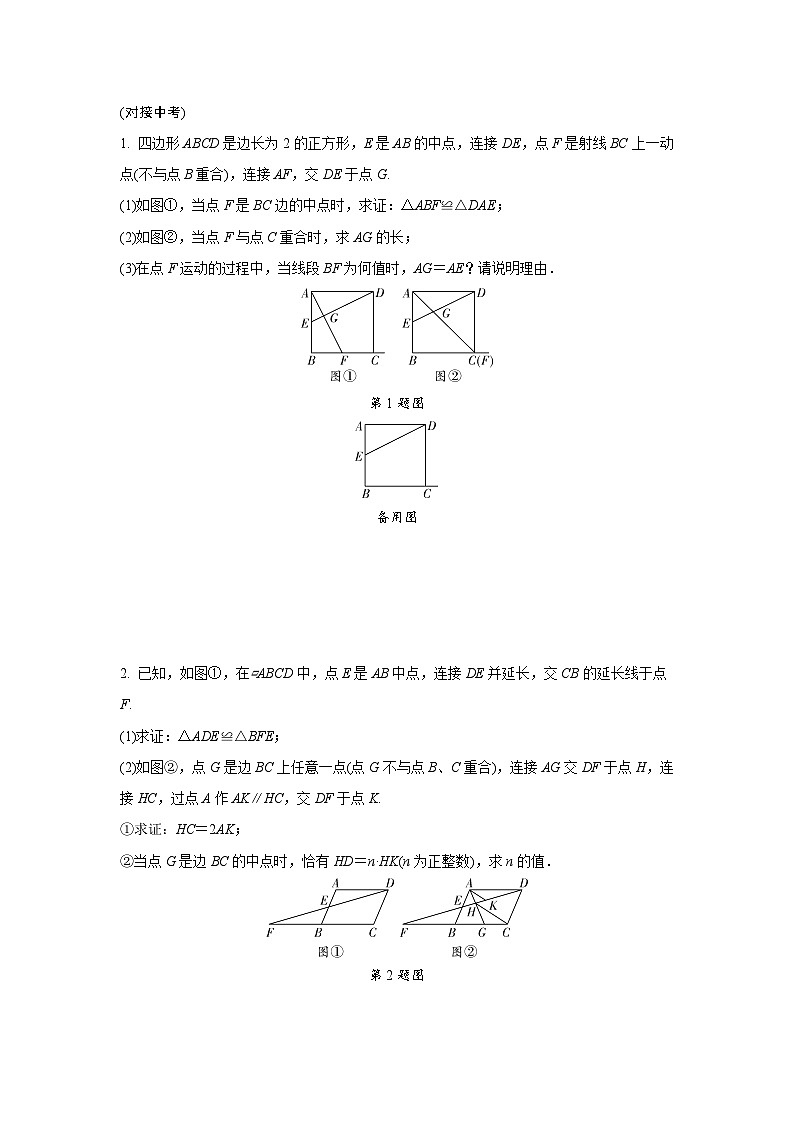
1. 四边形ABCD是边长为2的正方形，E是AB的中点，连接DE，点F是射线BC上一动点(不与点B重合)，连接AF，交DE于点G.
(1)如图①，当点F是BC边的中点时，求证：△ABF≌△DAE；
(2)如图②，当点F与点C重合时，求AG的长；
(3)在点F运动的过程中，当线段BF为何值时，AG＝AE？请说明理由．
第1题图
备用图
2. 已知，如图①，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F.
(1)求证：△ADE≌△BFE；
(2)如图②，点G是边BC上任意一点(点G不与点B、C重合)，连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K.
①求证：HC＝2AK；
②当点G是边BC的中点时，恰有HD＝n·HK(n为正整数)，求n的值．
第2题图
(针对训练)
1. 如图，边长为1的正方形ABCD中，点K在AD上，连接BK，过点A，C作BK的垂线，垂足分别为M，N，点O是正方形ABCD的中心，连接OM，ON.
第1题图
(1)求证：△ABM≌△BCN；
(2)请判定△OMN的形状，并说明理由；
(3)若点K在线段AD上运动(不包括端点)，当AK＝ eq \f(1,3) 时，求△OMN的面积．
2. 如图①，在正方形ABCD中，M是AD的中点，点E是边AB上的一个动点，连接EM并延长交射线CD于点F，过点M作EF的垂线交射线BC于点G，连接EG、FG.
(1)求证：△AME≌△DMF；
(2)在点E的运动过程中，探究：
①tan ∠GEF的值是否发生变化？若不变，求出这个值；
②如图②，把正方形ABCD改为矩形(AB