二项分布与超几何分布课件-2024届高考数学一轮复习

这是一份二项分布与超几何分布课件-2024届高考数学一轮复习，共33页。PPT课件主要包含了伯努利试验，ACD，变式演练，对点训练，ABC等内容，欢迎下载使用。
【课时目标】　理解二项分布、超几何分布，能判定随机变量是否服从 二项分布、超几何分布，会求它们的均值和方差；能够利用二项分布和 超几何分布解决简单的实际问题.【考情概述】　二项分布和超几何分布是两个基本的概率分布类型，是 新高考考查的热点，主要以解答题的形式进行考查，难度中等.
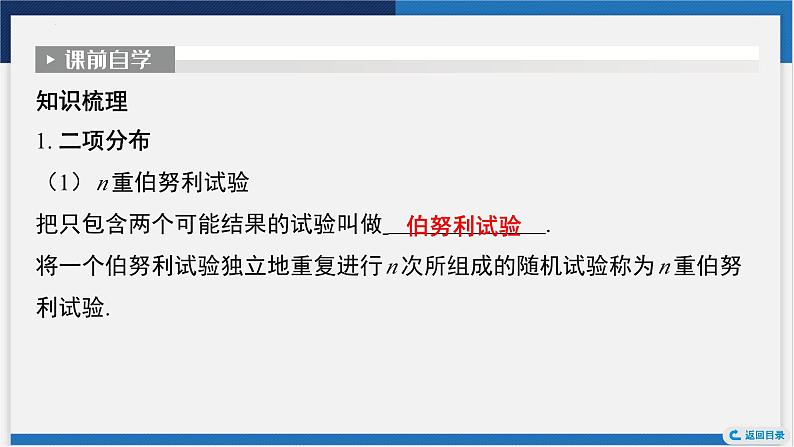
知识梳理1. 二项分布（1） n 重伯努利试验把只包含两个可能结果的试验叫做 ⁠.将一个伯努利试验独立地重复进行 n 次所组成的随机试验称为 n 重伯努 利试验.
（2） 二项分布的概念一般地，在 n 重伯努利试验中，设每次试验中事件 A 发生的概率为 p （0 ＜ p ＜1），用 X 表示事件 A 发生的次数，则 X 的分布列为 P （ X ＝ k ） ＝ （ k ＝0，1，2，…， n ）.如果随机变量 X 的 分布列具有上式的形式，那么称随机变量 X 服从二项分布，记作 X ～ ⁠.（3） 二项分布的均值与方差如果 X ～ B （ n ， p ），那么 E （ X ）＝ ， D （ X ）＝ ⁠ ⁠.
B （ n ， p ）　
np （1－
2. 两点分布（1） 两点分布的概念若随机变量 X 的分布列为
其中0＜ p ＜1，则称离散型随机变量 X 服从两点分布.（2） 两点分布的均值与方差若随机变量 X 服从两点分布，则 E （ X ）＝ ， D （ X ）＝ ⁠ ⁠.
如果随机变量 X 的分布列具有以上的形式，那么称随机变量 X 服从超几 何分布.（2） 超几何分布的均值从包含 M 件次品的 N 件产品中，不放回地随机抽取 n 件产品，若用 X 表 示抽取的 n 件产品中的次品数，则 E （ X ）＝ ⁠.
（3） （RA选三P59定义改编）若随机变量 X 的分布列为 P （ X ＝1）＝ 0.3， P （ X ＝2）＝0.7，则随机变量 X 服从两点分布.（　✕　）（4） （RA选三P81习题7.4第6题改编）有一个摸奖游戏，在一个袋子 中有10个红球、20个白球和30个黄球，这些球除颜色外完全相同，一次 从中随机地摸出5个球.若用 X 表示其中红球的个数，则 X 服从超几何分 布.（　√　）
2. （RA选三P78例5改编）一批零件共有30个，其中有3个不合格.若随机 从中抽取10个零件进行检测，则恰有1个不合格的概率为（　B　）
4. （多选）（RA选三P80习题7.4第1题改编）抛掷一颗质地均匀的骰 子，当朝上一面的点数是5或6时，就说这次试验成功.设30次试验中成 功的次数为 X ，则下列结论正确的是（　ACD　）
5. （RA选三P91复习参考题7第6题改编）已知每门大炮击中目标的概率 都是0.5.现在 n 门大炮同时对某一目标各射击一次.当 n ＝5时，恰好击中 目标3次的概率为 .如果使目标至少被击中一次的概率超过90％， 那么 n 的最小值为 ⁠.
（1） X 的分布列和数学期望；
（2） 甲答对几道题的概率最大.
解：所以 E （ X ）＝2.　（2） 由（1）中的分布列可知，甲答对2道题 的概率最大.
[拓展探究]将例1中“甲参加共有3道判断题的测试”改成“甲参加共有3 m （ m ∈N*）道判断题的测试”，问甲答对几道题的概率最大？
考向2　二项分布及变量间的线性关系例2　某企业从生产的一批零件中抽取100个作为样本，检测其质量指标 值 m （ m ∈[100，400]），得到如图所示的频率分布直方图.并依据质量 指标值划分等级如表所示.
以样本分布的频率作为总体分布的概率，解决下面的问题：
（1） 从生产的零件中随机抽取3个零件，记其中A级零件的个数为 X ， 求 X 的分布列和数学期望.
（2） 该企业为节省检测成本，采用混装的方式将所有零件按400个一 箱包装.已知1个A级零件的利润是12元，1个B级零件的利润是4元，试估 计每箱零件的利润.
解：（2） 设每箱零件中A级零件有 Y 个，则B级零件有（400－ Y ）个. 设每箱零件的利润为 Z 元，由题意知， Z ＝12 Y ＋4（400－ Y ）＝8 Y ＋ 1600.因为每个零件是A级零件的概率为0.9，每箱有400个零件，所以 Y ～ B （400，0.9）.所以 E （ Y ）＝400×0.9＝360.所以 E （ Z ）＝ E （8 Y ＋1600）＝8 E （ Y ）＋1600＝8×360＋1600＝4480.所以估计每箱 零件的利润为4480元.
1. 在例2的条件下，若一个A级零件的利润是12元，一个B级零件的利润 是4元，该企业采用混装的方式按箱包装，请问每箱至少装多少个零 件，才能使每箱的平均利润不低于1000元？
（多选）（2023·浙江联考）已知甲盒中有2个红球，1个蓝球，乙盒中 有1个红球，2个蓝球，这些球除颜色外都相同.从甲、乙两个盒子中各 取1个球放入原来为空的丙盒中.现从甲、乙、丙三个盒子中分别取1个 球，记从甲、乙、丙盒中取得红球的概率分别为 p 1， p 2， p 3，从甲、 乙、丙盒中取得红球的个数分别为 X 1， X 2， X 3，则下列结论中，正确 的是（　ABC　）
（2） 若不放回地从袋子里随机取出3个球，其中黑球的个数记为 X ，求 X 的分布列和数学期望.
2. 在例4（2）的条件下，若每次取出白球记3分，每次取出黑球记－2 分，不放回地从袋子里随机取出3个球，设总得分为 Y 分，则 Y 的期望 为 ⁠.3. 将例4（2）中的“不放回”变为“有放回”，则恰好取出2个黑球的 概率为 ⁠.