人教版高中数学必修第二册8.4——8.5同步测试滚动训练(含答案)

这是一份人教版高中数学必修第二册8.4——8.5同步测试滚动训练(含答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(本大题共8小题,每小题5分,共40分)
1.空间中,如果两个角的两条边分别对应平行,那么这两个角( )
A.相等B.互补
C.相等或互补D.不能确定
2.下列条件中能推出平面α与平面β平行的是( )
A.平面α内有无数条直线与β平行
B.平面α内的任意一条直线都与β平行
C.直线m∥α,m∥β,且直线m不在α内,也不在β内
D.直线m⊂α,直线l⊂β,且m∥β,l∥α
3.给出下列四个条件:
①空间中的三个点;②一条直线和一个点;③两条平行的直线;④两条垂直的直线.
其中能确定一个平面的是( )
A.①②③④B.①③
C.③④D.③
4.已知m,n,l1,l2表示直线,α,β表示平面,若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是( )
A.m∥β且l1∥αB.m∥β且n∥β
C.m∥β且n∥l2D.m∥l1且n∥l2
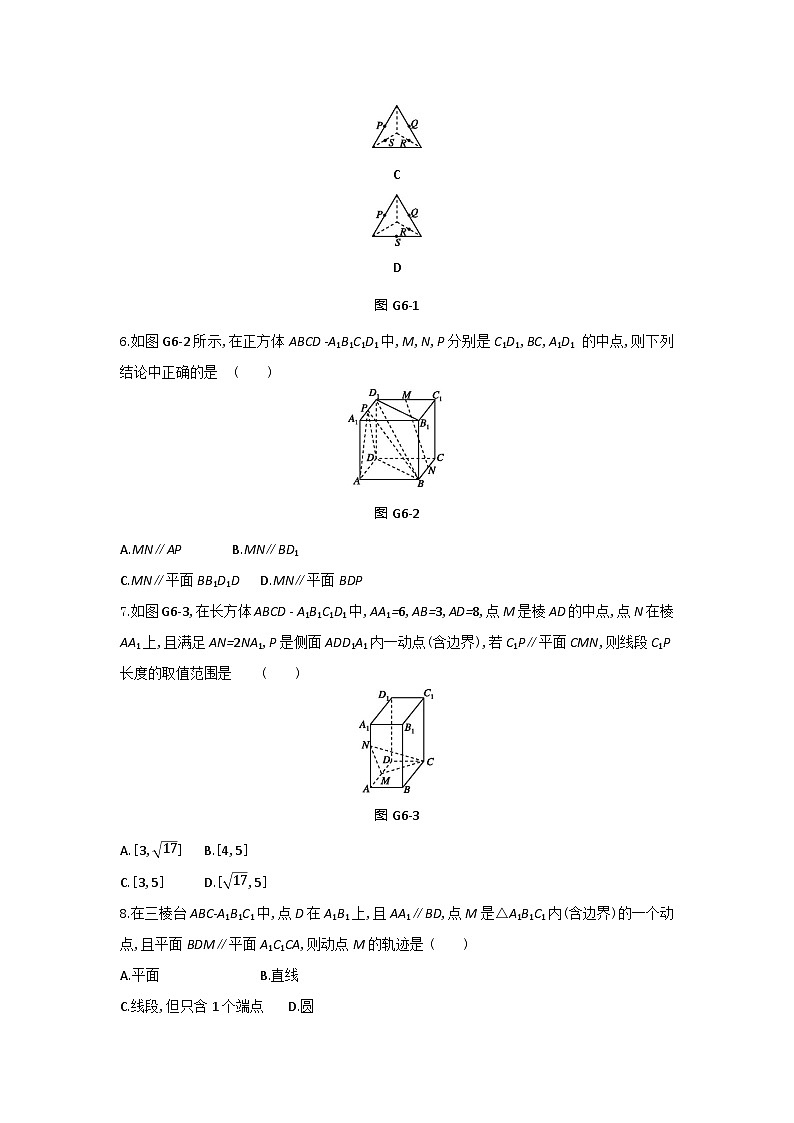
5.如图G6-1所示,P,Q,R,S分别是所在棱的中点,则这四个点不共面的是( )
A
B
C
D
图G6-1
6.如图G6-2所示,在正方体ABCD -A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1 的中点,则下列结论中正确的是( )
图G6-2
A.MN∥APB.MN∥BD1
C.MN∥平面BB1D1DD.MN∥平面BDP
7.如图G6-3,在长方体ABCD - A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )
图G6-3
A.[3,17]B.[4,5]
C.[3,5]D.[17,5]
8.在三棱台ABC-A1B1C1中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且平面BDM∥平面A1C1CA,则动点M的轨迹是( )
A.平面B.直线
C.线段,但只含1个端点D.圆
二、填空题(本大题共4小题,每小题5分,共20分)
9.空间三个平面之间的交线条数为n,则n的可能值为 .
10.过平面外一点作与该平面平行的平面有 个;过平面外一点作该平面的平行直线有 条.
11.如图G6-4,在正方体ABCD - A1B1C1D1中,M,N,P,Q,R,S分别是AB,BC,C1D1,C1C,A1B1,BB1的中点,给出下列说法:
①PQ与RS共面;②MN与RS共面;③PQ与MN共面.其中正确说法的序号是 .
图G6-4
12.在棱长为1的正方体ABCD - A1B1C1D1中,E,F分别是DD1和AB的中点,若平面B1EF交AD于点P,则PE= .
三、解答题(本大题共3小题,共40分)
13.(10分)正方体ABCD - A1B1C1D1如图G6-5所示.
(1)若E,F分别为AA1,CC1的中点,画出过点D1,E,F的截面;
(2)若M,N,P分别为A1B1,BB1,B1C1上的点(均不与B1重合),求证:△MNP是锐角三角形.
图G6-5
14.(15分)如图G6-6所示,在直四棱柱ABCD - A1B1C1D1中,底面ABCD是梯形,AB∥CD,CD=2AB,P,Q分别是CC1,C1D1的中点,求证:平面AD1C∥平面BPQ.
图G6-6
15.(15分)如图G6-7所示,四边形EFGH为四面体ABCD的一个截面,且该截面为平行四边形.
(1)求证:AB∥平面EFGH;
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
图G6-7
参考答案与解析
1.C [解析] 由等角定理知选C.
2.B [解析] 平面α内有无数条直线与β平行,则α与β相交或平行,故A不满足题意;平面α内的任意一条直线都与β平行,则平面α内一定有两条相交直线与平面β平行,则由面面平行的判定定理得α∥β,故B满足题意;直线m∥α,m∥β,且直线m不在α内,也不在β内,则α与β相交或平行,故C不满足题意;直线m⊂α,直线l⊂β,且m∥β,l∥α,则α与β相交或平行,故D不满足题意.故选B.
3.D [解析] 对于①,当这三个点共线时,经过这三个点的平面有无数个,故①不满足题意.对于②,当此点在此直线上时,有无数个平面经过这条直线和这个点,故②不满足题意.对于③,根据推论3可知两条平行直线唯一确定一个平面,故③满足题意.对于④,当这两条直线是异面直线时,这两条直线不同在任何一个平面内,不能确定一个平面,故④不满足题意.故选D.
4.D [解析] 由题意得,m,n 是平面α内的两条直线,l1,l2是平面β内的两条相交直线,要使α∥β,一个平面内有两条相交直线和另一个平面平行即可,故选D.
5.D [解析] 对于选项A,连接PS,QR,易证PS∥QR,∴P,S,R,Q四点共面;对于选项B,过P,S,R,Q可作一个正六边形,∴P,S,R,Q四点共面;对于选项C,连接PQ,RS,易证PQ∥RS,∴P,Q,R,S四点共面.故选D.
6.C [解析] 易知MN与AP是异面直线,故A中结论不正确.易知MN与BD1是异面直线,故B中结论不正确.连接AC,与BD交于点O,则O为BD的中点,连接OD1,ON.在正方体ABCD - A1B1C1D1中,∵M,N分别是C1D1,BC的中点,∴ON∥CD∥D1M,ON=12CD=D1M,∴四边形MNOD1为平行四边形,∴MN∥OD1.∵MN⊄平面BB1D1D,OD1⊂平面BB1D1D,∴MN∥平面BB1D1D,故C中结论正确.由选项C知MN∥平面BB1D1D,而平面BB1D1D和平面BDP相交,∴MN与平面BDP不平行,故D中结论不正确.故选C.
7.D [解析] 取A1D1的中点E,在DD1上取点F,使D1F=2DF,连接EF,C1E,C1F,则易知平面CMN∥平面C1EF.∵P是侧面ADD1A1内一动点(含边界),C1P∥平面CMN,∴P∈线段EF,∵C1E=C1D12+D1E2=5,C1F=C1D12+D1F2=5,∴当P与EF的中点重合时,线段C1P的长度取得最小值,当P与点E或点F重合时,线段C1P的长度取得最大值.取EF的中点O,连接C1O,则由题意知EF=42,C1O=C1E2-EO2=25−(22)2=17,∴线段C1P长度的取值范围是[17,5].故选D.
8.C [解析] 如图所示,在平面A1B1C1内,过D作DN∥A1C1,交B1C1于点N,连接BN.∵AA1∥BD,AA1⊂平面A1C1CA,BD⊄平面A1C1CA,∴BD∥平面A1C1CA.∵DN∥A1C1,DN⊄平面A1C1CA,A1C1⊂平面A1C1CA,∴DN∥平面A1C1CA.∵BD∩DN=D,∴平面BDN∥平面A1C1CA.∵点M是△A1B1C1内(含边界)的一个动点,且平面BDM∥平面A1C1CA,∴M的轨迹是线段DN,且M与D不重合,即动点M的轨迹是线段,但只含1个端点.故选C.
9.0,1,2,3 [解析] 三个平面可以互相平行,可以交于同一条直线,可以两个平面平行且被第三个平面所截,也可以两两相交,故答案为0,1,2,3.
10.1 无数 [解析] 过平面外一点作与该平面平行的平面,这样的平面有且只有1个.在符合题意的平面上过这个点的直线有无数条,这些直线都与原平面平行.
11.①③ [解析] 连接PR,QS,因为P,Q,R,S分别是C1D1,C1C,A1B1,B1B的中点,所以PRB1C1,QSB1C1,所以PRQS,所以四边形PRSQ是平行四边形,故①正确;连接QN,C1B,PM,则由题意得QN12C1BPM,所以PQ与MN共面,故③正确;因为MN与RS既不平行也不相交,故②错误.
12.136 [解析] 过点C1作C1G∥B1F,交CD于点G,过点E作HQ∥C1G,交CD的延长线于点H,交C1D1于点Q,连接B1Q,HF交AD于点P,则HQ∥B1F,所以Q,H,F,B1四点共面.由正方体的棱长为1,易知CG=BF=12.设D1Q=x,由题知HD=D1Q,因为C1Q∥HG,HQ∥C1G,所以四边形HQC1G为平行四边形,所以HG=QC1,即x+12=1-x,解得x=14.由题可知△PDH∽△PAF,所以APPD=AFHD=2,则PD=13.在Rt△PED中,可得PE=PD2+ED2=19+14=136.
13.解:(1)过点D1,E,F的截面如图所示.
(2)证明:设MB1=a,NB1=b,PB1=c,
则MN2=a2+b2,NP2=b2+c2,MP2=c2+a2,所以在△MNP中,cs M=MP2+MN2-NP22MP·MN=2a22MP·MN>0.
同理可得cs N>0,cs P>0.
故△MNP的三个内角均为锐角,即△MNP是锐角三角形.
14.证明:在直四棱柱ABCD - A1B1C1D1中,易知C1D1∥CD,C1D1=CD.
∵AB∥CD,∴AB∥C1D1,即D1Q∥AB.
∵Q为C1D1的中点,∴D1Q=12C1D1=12CD=AB,
∴四边形D1QBA为平行四边形,
∴AD1∥BQ,又AD1⊂平面AD1C,BQ⊄平面AD1C,∴BQ∥平面AD1C.
∵P,Q分别为CC1,C1D1的中点,∴PQ∥CD1,
又PQ⊄平面AD1C,CD1⊂平面AD1C,∴PQ∥平面AD1C.
∵BQ∩PQ=Q,∴平面AD1C∥平面BPQ.
15.解:(1)证明:∵四边形EFGH为平行四边形,∴EF∥HG,
又HG⊂平面ABD,EF⊄平面ABD,∴EF∥平面ABD.
∵EF⊂平面ABC,平面ABD∩平面ABC=AB,∴EF∥AB,
又AB⊄平面EFGH,EF⊂平面EFGH,∴AB∥平面EFGH.
(2)设EF=x(0∴CFCB=x4,则FG6=BFBC=BC-CFBC=1-x4,∴FG=6-32x,
∴四边形EFGH的周长l=2x+6-32x=12-x,
又0