2023_2024学年山东青岛莱西市六年级下学期期中数学试卷

这是一份2023_2024学年山东青岛莱西市六年级下学期期中数学试卷，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2023~2024学年山东青岛莱西市六年级下学期期中数学试卷
一、单选题
1.计算
A.
等于（
）
B. 1
C.
D.
2.已知三点M、N、G，画直线MN、画射线MG、连结NG，按照上述语句画图正确的是（ ）
A.
B.
C.
D.
3.下列运算正确的是（
A.
）．
B.
C.
D.
4.用简便方法计算
，下列变形正确的是（
）
A.
C.
B.
D.
下列各式中，计算结果等于 的是（
）
A.
B.
C.
D.
6.如图， 是线段
；（3）
的中点， 为线段
上一点，下列等式：（1）
；（2）
，其中正确的有（
）
A. 0个
B. 1个
C. 2个
D. 3个

7.如图所示，正方形网格中有
和
，如果每个小正方形的边长都为1，估测
与
的大小关系为（
）
A.
B.
C.
D. 无法估测
8.如图，OA的方向是北偏东15°，OB的方向是西北方向，若
，则OC的方向是（
）
A. 北偏东30°
B. 北偏东45°
C. 北偏东60°
D. 北偏东75°
2
2
2
2
9.选择计算（﹣4xy +3x y）（4xy +3x y）的最佳方法是（
）
A. 运用多项式乘多项式
法则
B. 运用平方差公式
C. 运用单项式乘多项式
法则
D. 运用完全平方公式
10.如图 ，将边长为 的大正方形剪去一个边长为 的小正方形（阴影部分），并将剩余部分沿虚线剪开，得到
两个长方形，再将这两个长方形拼成图 所示长方形．这两个图能解释下列哪个等式（ ）
A.
B.
C.
D.
二、填空题

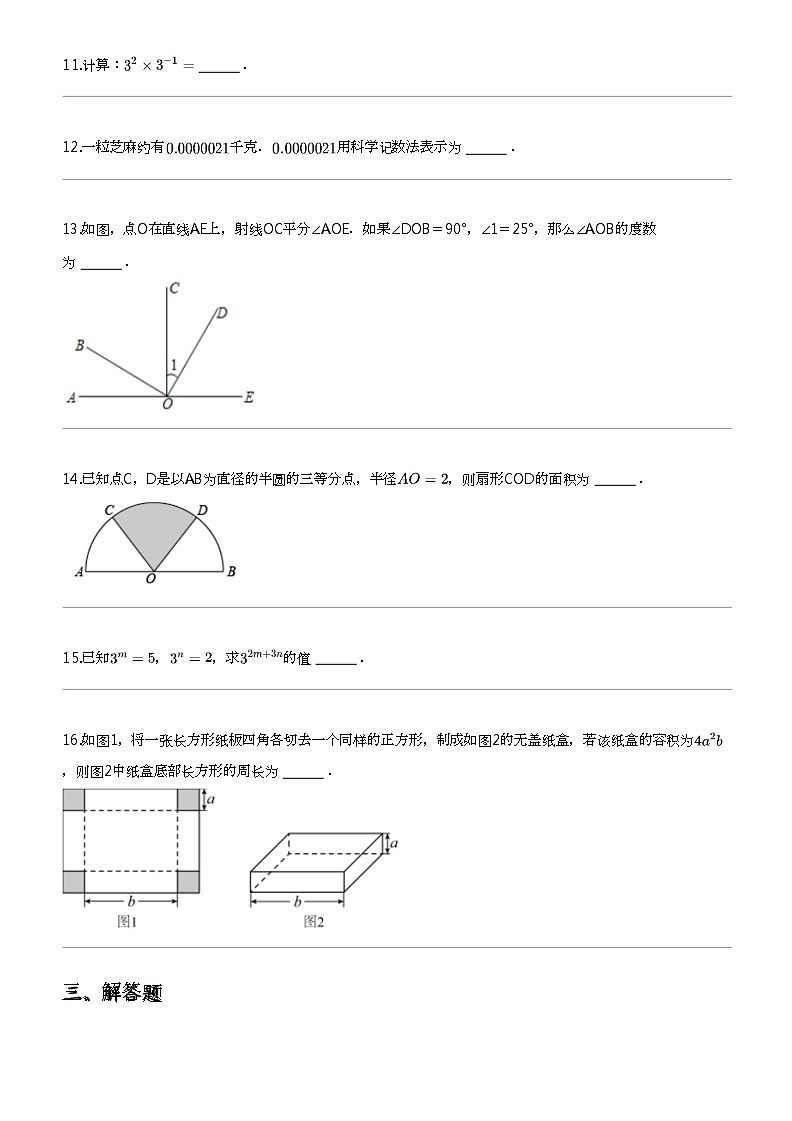
11.计算：
．
12.一粒芝麻约有
千克．
用科学记数法表示为
．
13.如图，点O在直线AE上，射线OC平分∠AOE．如果∠DOB＝90°，∠1＝25°，那么∠AOB的度数
为
．
14.已知点C，D是以AB为直径的半圆的三等分点，半径
，则扇形COD的面积为
．
15.已知
，
，求
的值
．
16.如图1，将一张长方形纸板四角各切去一个同样的正方形，制成如图2的无盖纸盒，若该纸盒的容积为
，则图2中纸盒底部长方形的周长为
．
三、解答题

17.计算
(1)
；
(2)
；
(3)
(4)
；
．
18.化简求值
(1)
(2)
，其中
，其中
，
．
，
．
19.如果整式
20.如图，
运算后不含 项，求m的值并计算结果．
，延长
到C，使
，宽为
，D是
，高为
的中点，求
的长度．
21.将如图所示的长为
史博物馆．
的大理石运往某地用以建设革命历
(1)求每块大理石的体积；（结果用科学记数法表示）
(2)如果一列火车总共运送了
科学记数法表示）
块大理石，共约重
千克，求每块大理石约重多少千克？（结果用
22.如图，某市有一块长为
间将修建一座雕像．
米，宽为
米的长方形地块，规划部门计划将阴影部分进行绿化，中

(1)求绿化的面积是多少平方米？（用代数式表示）
(2)求出当 时的绿化面积．
，
23.如图，将直角三角板OMN的直角顶点O放在直线AB上，射线OC平分
．
(1)当
(2)若
时，求
，求
的度数；
的度数．
24.在数学中，有许多关系都是在不经意间被发现的，请认真观察图形，解答下列问题：
(1)如图1，用两种不同的方法表示阴影图形的面积，得到一个等量关系：
．
2
2
(2)若图1中a、b满足a+b＝7，ab＝10，求a +b 的值；
(3)如图2，C是线段AB上一点，以AC，BC为边向两边作正方形，AC+BC=8，两正方形面积和S +S ＝40，求
1
2
图中阴影部分面积．
25.“时钟里的数学问题”：时钟是我们日常生活中常用的生活用品，钟表上的时针和分针都绕其轴心旋转，表
盘中数字 均匀分布，分针转动一周（ ）需要60分钟，时针转动一周的 需要60分钟，这样，分针
的转速为每分钟转6度，时针的转速为每分钟转 度．
课题学习：

时，时针与分针所成角度多少度？解决这个问题，可以先考虑三点整，时针与分针所成角度为
；从
到
，我们可以先计算分针转动的角度，
．故 时，时针与分针所成角度是
，时针转动的角度，
．
，
问题解决：
(1)当
(2)如图1，盘上的点A对应数字“12”，点B对应数字“3”，若分针
钟， 第一次平分
(3)当时针和分针所成角度
时，时针与分针所成角度是____________；
从
的位置开始转动，经过多少分
；
时形成一条直线，这条直线刚好平分钟面，我们将这样的时刻称为“美妙时
刻”，如图3，六点整就是一个美妙时刻，从0时到24时共有____________个美妙时刻．
26.规定两数a，b之间的一种运算，记作
．
：如果
，那么
．例如：因为
，所以
(1)根据上述规定完成填空：
____________，
____________，
____________；
(2)小明在研究这种运算时发现一个现象：
，小明给出了如下的理由：
设
，则
，即
，即
．
所以
所以
．
．
请你尝试运用这种方法判断
是否成立，并说明理由．