江西省吉安市青原区2024年中考数学一模试卷

这是一份江西省吉安市青原区2024年中考数学一模试卷，共7页。

考试时间：分钟 满分：分
*注意事项：
1、填写答题卡的内容用2B铅笔填写2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
一、单项选择题（本大题共6小题，每小题3分，共18分）在每小题列出的四个备选项中只有一项是最符合题目要求的，请将其代码填涂在答题卡相应位置．错选，多选或未选均不得分．(共6题；共18分)
1. 下列各数中，最大的数是（ ）
2. 2024年我省政府工作报告中，梳理了2023年关于民生福祉的工作业绩，其中在教育方面我省义务教育学位新增27.4万个，将27.4万用科学记数法表示应为（ ）
3. 如图所示，由三个完全相同的小正方体搭成的几何体，它的俯视图为（ ）
4. 下列运算正确的是（ ）
5. 如图， ， 平分 ， ， ， 则的度数为（ ）
6. 如图，矩形中， ， ， 点E在矩形的边上，则当的一个内角度数为时，符合条件的点E的个数共有（ ）
二、填空题（本大题共6小题，每小题3分，共18分）(共6题；共18分)
7. 的绝对值是____________________.
8. 已知方程的两个根分别为 ， ， 则的值为____________________．
9. 如图所示，若入射光线与平面镜成夹角，且入射光线与反射光线与平面镜所成的角度相等，则入射光线与反射光线的夹角的度数为____________________．
10. 古印度数学家所著的《算法本原》一本中记载了一个有趣的猴群问题：一群猴子在树林中玩耍，总数的八分之一的平方只猴子在欢乐地蹦跳；还有12只猴子在啼叫，设这群猴子共有x只，根据题意，可列方程为____________________．
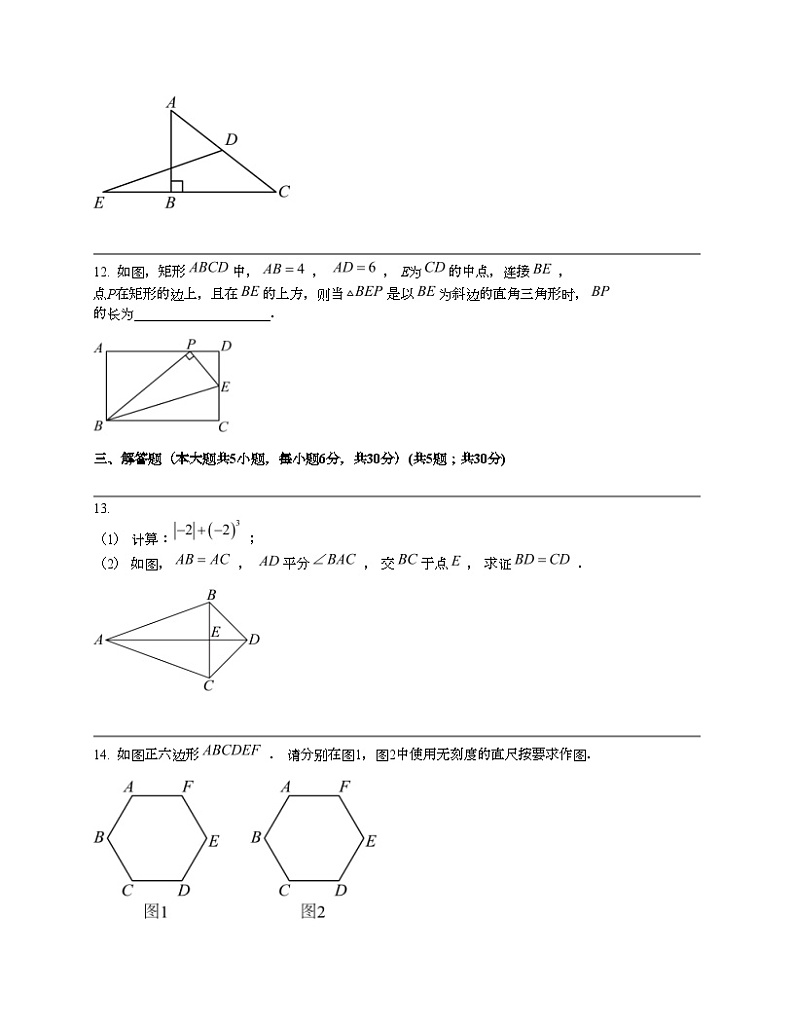
11. 如图，中， ， D为的中点，延长至E ， 使 ， 若 ， 则的度数为____________________．
12. 如图，矩形中， ， ， E为的中点，连接 ， 点P在矩形的边上，且在的上方，则当是以为斜边的直角三角形时，的长为____________________．
第Ⅱ卷 主观题
第Ⅱ卷的注释
三、解答题（本大题共5小题，每小题6分，共30分）(共5题；共30分)
13.
（1） 计算：；
（2） 如图， ， 平分 ， 交于点 ， 求证 ．
14. 如图正六边形 ． 请分别在图1，图2中使用无刻度的直尺按要求作图．
（1） 在图1中，以为直角边，作一个直角三角形；
（2） 在图2中，以为边作一个菱形．
15. 计算： ， 下面是某同学的解答过程：
解：原式…………………第一步
…………………第二步
（1） 第一步的依据是____________________，运用的方法是____________________，第二步的依据是____________________；
①分式的基本性质；②分式的加减法则；③分式的通分；④分式的约分法则．
（2） 计算： ．
16. 如图，点A反比例函数的图象上，点C在x轴上，轴，垂足为B ， ， ， ， 交反比例函数的图象于点D ．
（1） 求反比例函数的解析式；
（2） 求点D的坐标．
17. 某地爱心驿站招募志愿者3人，共有20人报名，小李和小王两男同学报了名．由于报名者都符合条件，故采取抽签的方式决定，所招募的3个志愿者中要求两女一男，于是共做20个签，其中两个写有的“女”的签、一个写有“男”的签，17个未写任何字的空签，每个签从外观上无任何差别．
（1） 若小李先抽，正好抽到的是“男”签概率为____________________；
（2） 若小李和小王两人分别在第17和18个抽，此时只有四个签，其中只有一个“女”签和一个“男”签，另两个为空签，求小李或小王抽到“男”签的概率．
四、解答题（本大题共3小题，每小题8分，共24分）(共3题；共24分)
18. 为鼓励学生加强强身健体，某校计划购买一批篮球和排球，根据学校实际，决定共购买30个排球，20个篮球，共花费2560元，若篮球和排球的单价之和为104元．
（1） 求篮球和排球的单价；
（2） 据不完全统计，每个学年篮球的损耗率是排球的损耗率的两倍，若学期末这批篮球和排球最少剩下43个，求排球的最大损耗率．
19. 如图1是某地公园里的一座纪念碑，将其抽象为图2，已知 ， ， ， ， ， （结果精确到小数点后一位）
（1） 求证：；
（2） 求纪念碑的高度．
（参考数据： ， ， ， ， ， ． ）
20. 如图，在中， ， 以为直径的与线段交于点 ， 作 ， 垂足为 ， 的延长线与的延长线交于点F ．
（1） 求证：直线是的切线：
（2） 若 ， ， 求长．
五、解答题（本大题共2小题，每小题9分，共18分）(共2题；共18分)
21. 某校为了有效提升学生综合素质，同时减轻学生课业负担，决定在全校开展丰富多彩的学生课外活动，经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书共五类项目，并在组织活动前进行了初步调查，调查要求在以上五类项目中只能选一项最感兴趣的一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的统计图，请解答下列问题：
（1） 求m的值；
（2） 补全条形统计图；
（3） 求“社会实践”所对扇形圆心角的度数；
（4） 已知该校共有1200名学生，请你估计该校最喜欢读书活动的学生数，根据统计图中的数据，请你针对课外活动提出一条合理化建议．
22. 如图
（1） 课本再现
在学习了平行四边形的概念后，进一步得到平行四边形的性质：平行四边形的对角线互相平分．
如图1，在平行四边形中，对角线与交于点O ， 求证： ， ．
（2） 知识应用
在中，点P为的中点．延长到D ， 使得 ， 延长AC到E ， 使得 ， 连接 ． 如图2，连接 ， 若 ， 请你探究线段与线段之间的数量关系．写出你的结论，并加以证明．
六、解答题（本大题共12分）(共1题；共12分)
23. 综合与实践
问题提出
如图1，在中， ， ， 点D在上， ， 点P沿折线运动（运动到点C停止），以为边作正方形 ． 设点P运动的线路长为x ， 正方形的面积为y ．
初步感悟
（1） 当点P在上运动时，若 ， 则
①____________________，y关于x的函数关系式为____________________；
②连接 ， 则长为____________________．
（2） 当点P在上运动时，求y关于x的函数解析式．
（3） 延伸探究
如图2，将点P的运动过程中y与x的函数关系绘制成如图2所示的图象，请根据图象信息，解决如下问题：
①当点P的运动到使时，图像上对应点的坐标为 ▲ ；
②当将正方形分成面积相等的两部分时，与正方形交于点G、H两点，请直接写出此时的长，以及自变量和函数的值．A . 0
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A . 4个
B . 5个
C . 6个
D . 7个