江西省萍乡市2023-2024学年高二下学期期中考试数学试题

这是一份江西省萍乡市2023-2024学年高二下学期期中考试数学试题，共4页。

考试时间：分钟 满分：分
*注意事项：
1、填写答题卡的内容用2B铅笔填写2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
一、/span>､单项选择题：本大题共8小题，每小题5分，共40分.每小题给出的四个选项中，只有一项是符合题目要求的.(共8题；共40分)
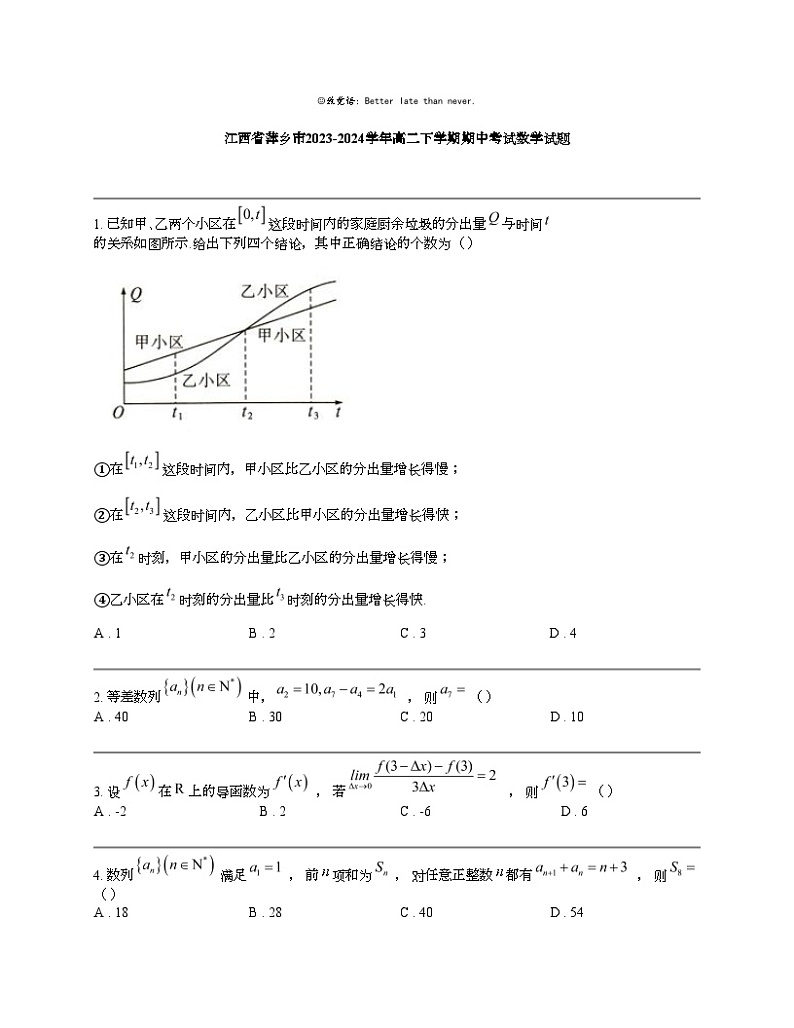
1. 已知甲､乙两个小区在这段时间内的家庭厨余垃圾的分出量与时间的关系如图所示.给出下列四个结论，其中正确结论的个数为（ ）
①在这段时间内，甲小区比乙小区的分出量增长得慢；
②在这段时间内，乙小区比甲小区的分出量增长得快；
③在时刻，甲小区的分出量比乙小区的分出量增长得慢；
④乙小区在时刻的分出量比时刻的分出量增长得快.
2. 等差数列中， ， 则（ ）
3. 设在上的导函数为 ， 若 ， 则（ ）
4. 数列满足 ， 前项和为 ， 对任意正整数都有 ， 则（ ）
5. 等比数列中， ， 函数的导函数为 ， 则（ ）
6. 我国古代《洛书》中记载着一种三阶幻方：将九个数字填入一个的正方形方格，满足每行､每列､每条对角线上的三个数字之和相同（如图）.已知数列的通项公式为 ， 现将该数列的前16项填入一个的正方形方格，使其满足四阶幻方，则此四阶幻方中每一行的数字之和为（ ）
7. 对于三次函数 ， 给出定义：是的导函数，是的导函数，若方程有实数解 ， 则称点为函数的“拐点”.经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.设函数 ， 则（ ）
8. 对于任意实数 ， 不等式恒成立，则集合的一个子集为（ ）
二、/span>､多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.(共3题；共18分)
9. 等比数列满足 ， 公比为2，数列满足 ， 下列说法正确的是（ ）
10. 奇函数满足对于任意 ， 有 ， 其中为的导函数，则下列不等式成立的是（ ）
11. 已知 ， 若函数的三个不同零点依次构成等差数列，则下列结论正确的是（ ）
三、/span>､填空题：本大题共3小题，每小题5分，共15分.(共3题；共15分)
12. 已知函数 ， 则____________________.
13. 足球世界杯小组赛中，同一小组的每支队伍都必须和组内其他队伍各进行一场比赛，比如组中有4支队伍，则该组需要进行6场比赛.按此规则，设一个含有支球队的小组中进行的所有比赛场次为场，则____________________.
14. 已知函数 ， 当时，恒成立，则实数的取值范围为____________________.
第Ⅱ卷 主观题
第Ⅱ卷的注释
四、/span>､解答题：本大题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.(共5题；共77分)
15. 已知数列的前项和为 ， 且满足.
（1） 求的值；
（2） 试猜想的通项公式，并证明.
16. 已知函数.
（1） 若函数 ， 求在点处的切线方程；
（2） 试判断的单调性，并证明；
（3） 证明：.
17. 正项等差数列的公差与正项等比数列的公比相同，且 ， ， 数列满足.
（1） 求的通项公式；
（2） 求的前项和.
18. 函数.
（1） 讨论函数的单调性；
（2） 若函数图象上存在两点 ， 且 ， 使得 ， 则称为“拉格朗日中值函数”，并称线段的中点为函数的一个“拉格朗日平均值点”.试判断函数是否为“拉格朗日中值函数”？若是，判断函数的“拉格朗日平均值点”的个数；若不是，请说明理由.
19. 函数.
（1） 当时，求的极值点个数；
（2） 若时，单调递减，求的取值范围；
（3） 求证：.
A . 1
B . 2
C . 3
D . 4
A . 40
B . 30
C . 20
D . 10
A . -2
B . 2
C . -6
D . 6
A . 18
B . 28
C . 40
D . 54
A . -8
B . 4
C . -2
D . 0
A . 60
B . 72
C . 76
D . 80
A . 2022
B . 2023
C . 2024
D . 2025
A .
B .
C .
D .
A . 为递增数列
B . 为递增数列
C . 中最小项的值为1
D .
A .
B .
C .
D .
A .
B .
C .
D .