

四川省金堂县金龙中学北师版八下数学期末数学模拟试卷 (含解析)
展开考卷信息:
本卷试题共 26 题,单选 12题,填空6题,解答8题,满分 120 分,限时120分钟,本卷题型针对性较高,覆盖面题有深度,可衡量学生掌握本册内容的具体情况!
一.单项选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )
A.B.C.D.
2.若a<b,则下列结论成立的是( )
A.a+2>b+2B.﹣2a<﹣2bC.3a>3bD.1﹣a>1﹣b
3.只用同一种正多边形铺满地面,不可以选择( )
A.正六边形B.正五边形C.正四边形D.正三角形
4.下列各式分解因式正确的是( )
A.9x2﹣1=(9x﹣1)(9x+1)
B.a4﹣1=(a2+1)(a2﹣1)
C.﹣81a2﹣b2=﹣(9a﹣b)(9a+b)
D.(ab+a)﹣1﹣b=(a﹣1)(b+1)
5.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点B.三条角平分线的交点
C.三边中垂线的交点D.三边上高的交点
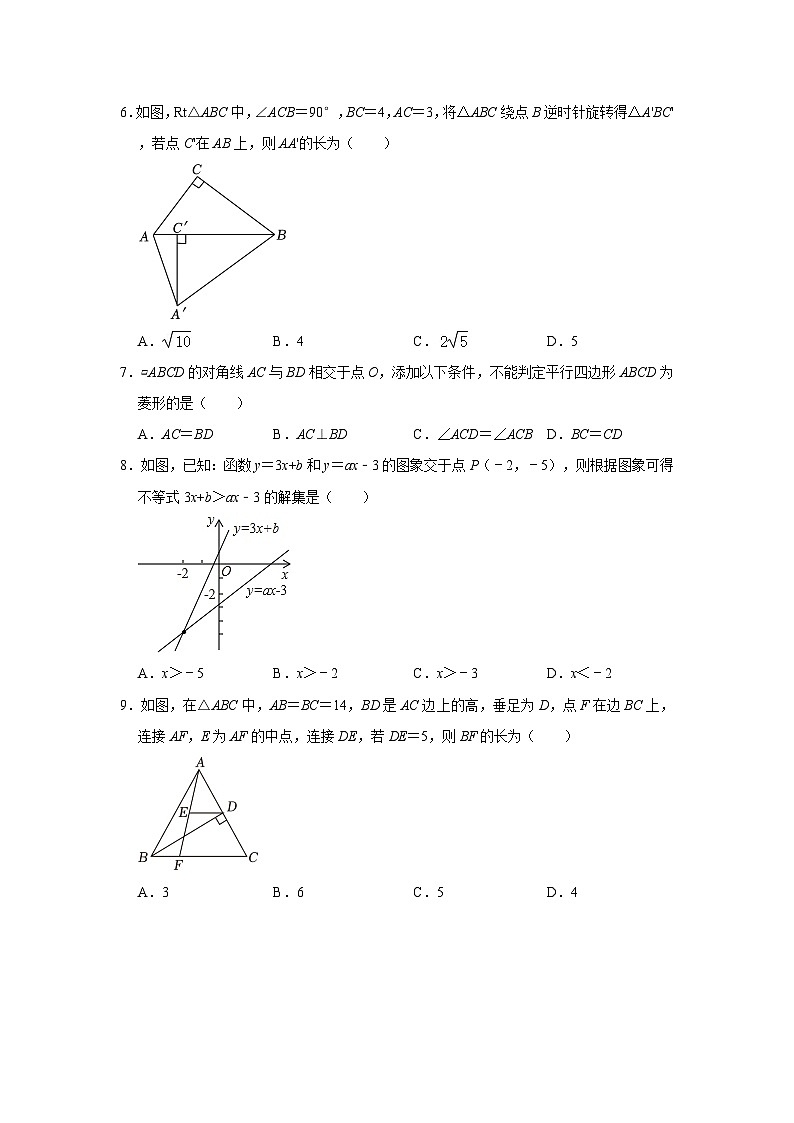
6.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得△A'BC',若点C'在AB上,则AA'的长为( )
A.B.4C.D.5
7.▱ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC=BDB.AC⊥BDC.∠ACD=∠ACBD.BC=CD
8.如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5B.x>﹣2C.x>﹣3D.x<﹣2
9.如图,在△ABC中,AB=BC=14,BD是AC边上的高,垂足为D,点F在边BC上,连接AF,E为AF的中点,连接DE,若DE=5,则BF的长为( )
A.3B.6C.5D.4
10.如图,已知A,B的坐标分别为(1,2),(3,0),将△OAB沿x轴正方向平移,使B平移到点E,得到△DCE,若OE=4,则点C的坐标为( )
A.(2,2)B.(3,2)C.(1,3)D.(1,4)
11.若关于x的方程=2的解为正数,则m的取值范围是( )
A.m<6B.m>6C.m>6且m≠10D.m<6且m≠2
12.如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC,CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE;⑤S△CEF=S△ABE.其中正确的是( )
A.①②③B.①②④C.②③④D.①②⑤
二、填空题(本题共6小题,每小题2分,共12分.)
13.因式分解:6x2﹣9xy= .
14.若分式的值为0,则x= .
15.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到△DEF,若四边形ABED的面积为20,则平移距离为 .
16.如图,直线y1=﹣x+a与y2=bx﹣4相交于点P,已知点P的坐标为(1,﹣3),则关于x的不等式﹣x+a≤bx﹣4的解集是 .
17.宜宾市与甲、乙两地的距离分别为320千米和250千米,从宜宾市开往甲地高铁的速度比从宜宾市开往乙地高铁的速度快70千米/时,结果从宜宾市到甲、乙两地所需时间相同.求从宜宾市到甲、乙两地高铁的速度分别是多少千米/时?设从宜宾市开往乙地高铁的速度为x千米/时,则可列方程为 .
18.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
三、解答题(本题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)解不等式组:.
20.(8分)先化简,再求值:(﹣1)÷,其中x=3.
21.(8分)在如图所示的直角坐标系中,画图并解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求△ABC的面积.
22.(8分)如图,平行四边形ABCD中,BD是它的一条对角线过A,C两点作AE⊥BD,CF⊥BD,垂足分别为E,F,延长AE,CF分别交CD,AB于M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求BN的长.
23.(10分)【三角形中位线定理】
已知:在△ABC中,点D,E分别是边AB,AC的中点.直接写出DE和BC的关系;
【应用】
如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,若BC=5,CD=3,EF=2,∠AFE=45°,求∠ADC的度数;
【拓展】
如图,在四边形ABCD中,AC与BD相交于点E,点M,N分别为AD,BC的中点,MN分别交AC,BD于点F,G,EF=EG.
求证:BD=AC.
24.(10分)新华书店决定用不多于28000元购进甲乙两种图书共1200本进行销售,已知甲种图书进价是乙种图书每本进价的1.4倍,若用1680元购进甲种图书的数量比用1400元购进的乙种图书的数量少10本.
(1)甲乙两种图书的进价分别为每本多少元?
(2)新华书店决定甲种图书售价为每本40元,乙种图书售价每本30元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完)
25.(10分)阅读材料:要将多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,再把它的后两项分成一组,从而得到:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n),这时a(m+n)+b(m+n)中又有公因式(m+n),于是可以提出(m+n),从而得到(m+n)(a+b),因此有am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.请回答下列问题:
(1)尝试填空:2x﹣18+xy﹣9y= ;
(2)解决问题:因式分解;ac﹣bc+a2﹣b2.
(3)拓展应用:已知三角形的三边长分别是a,b,c,且满足a2﹣2ab+2b2﹣2bc+c2=0,试判断这个三角形的形状,并说明理由.
26.(10分)在△ABC中,AB=AC,∠BAC=90°,点D在边BC上.
(1)如图1,将线段AD绕着点A顺时针旋转90°,得到线段AE,连接EB,判断线段EB,BD,AD的数量关系,并证明;
(2)在图2中,在线段BD取一点F,使得DF=DC,以BF为斜边向△ABC外作等腰直角三角形BGF,连接AG.
①补全图形;
②判断线段AG与AD的数量关系,并证明.
参考答案与详细解析
考卷信息:
本卷试题共 26 题,单选 12题,填空6题,解答8题,满分 120 分,限时120分钟,本卷题型针对性较高,覆盖面题有深度,可衡量学生掌握本册内容的具体情况!
一.单项选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )
A.B.
C.D.
【答案】B
【解答】解:选项A、C、D不能找到这样的一个点,使这些图形绕某一点旋转180°后与原来的图形重合,所以它们不是中心对称图形;
选项B能找到这样的一个点,使这个图形绕某一点旋转180°后与原来的图形重合,所以它是中心对称图形;
故选:B.
2.若a<b,则下列结论成立的是( )
A.a+2>b+2B.﹣2a<﹣2bC.3a>3bD.1﹣a>1﹣b
【答案】D
【解答】解:A、a<b,则a+2<b+2,选项说法错误,不符合题意;
B、a<b,则﹣2a>﹣2b,选项说法错误,不符合题意;
C、a<b,则3a<3b,选项说法错误,不符合题意;
D、a<b,则1﹣a>1﹣b,选项说法正确,符合题意;
故选:D.
3.只用同一种正多边形铺满地面,不可以选择( )
A.正六边形B.正五边形C.正四边形D.正三角形
【答案】B
【解答】解:A、正六边形的每个内角是120°,能整除360°,3个能密铺,故不符合题意;
B、正五边形的每个内角是108°,不能整除360°,不能密铺,故符合题意;
C、正方形的每个内角是90°,4个能密铺,故不符合题意;
D、正三角形的每个内角是60°,能整除360度,6个能密铺,故不符合题意;
故选:B.
4.下列各式分解因式正确的是( )
A.9x2﹣1=(9x﹣1)(9x+1)
B.a4﹣1=(a2+1)(a2﹣1)
C.﹣81a2﹣b2=﹣(9a﹣b)(9a+b)
D.(ab+a)﹣1﹣b=(a﹣1)(b+1)
【答案】D
【解答】解:A.9x2﹣1=(3x+1)(3x﹣1)≠(9x﹣1)(9x+1),故选项A分解错误;
B.a4﹣1=(a2+1)(a2﹣1)=(a2+1)(a+1)(a﹣1),故选项B分解错误;
C.﹣81a2﹣b2=﹣(81a2+b2)≠(9a﹣b)(9a+b),故选项C分解错误;
D.(ab+a)﹣1﹣b=a(b+1)﹣(1+b)=(a﹣1)(b+1),故选项D分解正确.
故选:D.
5.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点B.三条角平分线的交点
C.三边中垂线的交点D.三边上高的交点
【答案】C
【解答】解:∵三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最适当.
故选:C.
6.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得△A'BC',若点C'在AB上,则AA'的长为( )
A.B.4C.D.5
【答案】A
【解答】解:∵将△ABC绕点B逆时针旋转得△A′BC',
∴∠A'C'B=∠C=90°,A'C'=AC=3,AB=A'B,
根据勾股定理得:
AB==5,
∴A'B=AB=5,
∴AC'=AB﹣BC'=1,
在Rt△AA'C'中,由勾股定理得:
AA'==,
故选:A.
7.▱ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC=BDB.AC⊥BDC.∠ACD=∠ACBD.BC=CD
【答案】A
【解答】解:A、AC=BD时,▱ABCD是矩形,故选项A符合题意;
B、AC⊥BD时,▱ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠ACD=∠ACB,
∴∠DAC=∠ACD,
∴AD=CD,
∴▱ABCD是菱形,故选项C不符合题意;
D、BC=CD时,▱ABCD是菱形,故选项D不符合题意;
故选:A.
8.如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5B.x>﹣2C.x>﹣3D.x<﹣2
【答案】B
【解答】解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
则根据图象可得不等式3x+b>ax﹣3的解集是x>﹣2,
故选:B.
9.如图,在△ABC中,AB=BC=14,BD是AC边上的高,垂足为D,点F在边BC上,连接AF,E为AF的中点,连接DE,若DE=5,则BF的长为( )
A.3B.6C.5D.4
【答案】D
【解答】解:∵BC=14,
∴FC=BC﹣BF=14﹣BF.
∵AB=BC,BD⊥AC,
∴AD=DC,
∵AE=EF,
∴DE是△AFC的中位线,
∴DE=FC=5.
∴FC=10.
∴14﹣BF=10.
∴BF=4.
故选:D.
10.如图,已知A,B的坐标分别为(1,2),(3,0),将△OAB沿x轴正方向平移,使B平移到点E,得到△DCE,若OE=4,则点C的坐标为( )
A.(2,2)B.(3,2)C.(1,3)D.(1,4)
【答案】A
【解答】解:∵B(3,0),
∴OB=3,
∵OE=4,
∴BE=OE﹣OB=1,
∴将△OAB沿x轴正方向平移1个单位得到△DCE,
∴点C是将A向右平移1个单位得到的,
∴点C是的坐标是(1+1,2),即(2,2).
故选:A.
11.若关于x的方程=2的解为正数,则m的取值范围是( )
A.m<6B.m>6C.m>6且m≠10D.m<6且m≠2
【答案】D
【解答】解:关于x的方程=2的解为:x=,
∵原方程有可能产生增根2,
∴,
∴m≠2.
∵关于x的方程=2的解为正数,
∴,
∴m<6.
综上,m的取值范围是:m<6且m≠2.
故选:D.
12.如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC,CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE;⑤S△CEF=S△ABE.其中正确的是( )
A.①②③B.①②④C.②③④D.①②⑤
【答案】D
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);
①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF.
若AD与BF相等,则BF=BC,
题中未限定这一条件,
若S△BEF=S△ACD;则S△BEF=S△ABC,
则AB=BF,
∴BF=BE,题中未限定这一条件,
∴④不一定正确.
若AD与AF相等,即∠AFD=∠ADF=∠DEC,
即EC=CD=BE
即BC=2CD,
题中未限定这一条件,
∴③不一定正确,
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;⑤正确;
故选:D.
填空题(本题共6小题,每小题2分,共12分.)
13.因式分解:6x2﹣9xy= 3x(2x﹣3y) .
【答案】3x(2x﹣3y).
【解答】解:原式=3x•2x﹣3x•3y
=3x(2x﹣3y).
故答案为:3x(2x﹣3y).
14.若分式的值为0,则x= 2 .
【答案】2.
【解答】解:由分式的值为零的条件得x﹣2=0且x﹣4≠0,
解得x=2且x≠4,
∴x=2.
故答案为:2.
15.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到△DEF,若四边形ABED的面积为20,则平移距离为 4 .
【答案】4.
【解答】解:在Rt△ABC中,∵∠ABC=30°,
∴AC=AB=5,
∵△ABC沿CB向右平移得到△DEF,
∴AD=BE,AD∥BE,
∴四边形ABED为平行四边形,
∵四边形ABED的面积等于20,
∴AC•BE=20,即5BE=20,
∴BE=4,
即平移距离等于4.
故答案为:4.
16.如图,直线y1=﹣x+a与y2=bx﹣4相交于点P,已知点P的坐标为(1,﹣3),则关于x的不等式﹣x+a≤bx﹣4的解集是 x≥1 .
【答案】x≥1.
【解答】解:∵直线y1=﹣x+a与y2=bx﹣4相交于点P,已知点P的坐标为(1,﹣3),
∴关于x的不等式﹣x+a≤bx﹣4的解集是x≥1.
故答案为:x≥1.
17.宜宾市与甲、乙两地的距离分别为320千米和250千米,从宜宾市开往甲地高铁的速度比从宜宾市开往乙地高铁的速度快70千米/时,结果从宜宾市到甲、乙两地所需时间相同.求从宜宾市到甲、乙两地高铁的速度分别是多少千米/时?设从宜宾市开往乙地高铁的速度为x千米/时,则可列方程为 = .
【答案】=.
【解答】解:设从宜宾市开往乙地高铁的速度为x千米/时,则从宜宾市开往甲地高铁的速度为(x+70)千米/时,
根据题意可得=.
故答案为:=.
18.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 2 .
【答案】见试题解答内容
【解答】解:连接DN、DB,如图所示:
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD===4,
∵点E,F分别为DM,MN的中点,
∴EF是△DMN的中位线,
∴EF=DN,
由题意得,当点N与点B重合时DN最大,最大值为4,
∴EF长度的最大值为2,
故答案为:2.
三、解答题(本题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)解不等式组:.
【答案】1<x<5.
【解答】解:,
解不等式①,得x>1;
解不等式②,得 x<5;
∴原不等式组的解集为1<x<5.
(8分)先化简,再求值:(﹣1)÷,其中x=3.
【答案】见试题解答内容
【解答】解:原式=(﹣)•
=•
=x+2,
当x=3时,原式=3+2=5.
21.(8分)在如图所示的直角坐标系中,画图并解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求△ABC的面积.
【答案】(1)A(2,0),B(﹣1,﹣4);
(2)见解答;
(3).
【解答】解:(1)A(2,0),B(﹣1,﹣4);
(2)如图,△AB1C1为所作,
(3)△ABC的面积=4×4﹣﹣﹣=.
22.(8分)如图,平行四边形ABCD中,BD是它的一条对角线过A,C两点作AE⊥BD,CF⊥BD,垂足分别为E,F,延长AE,CF分别交CD,AB于M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求BN的长.
【答案】见试题解答内容
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴CM∥AN,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴四边形AMCN是平行四边形;
(2)解:∵四边形AMCN是平行四边形,
∴CM=AN,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴DM=BN,∠MDE=∠NBF,
在△MDE和△NBF中,
,
∴△MDE≌△NBF(AAS),
∴DE=BF=4,
在Rt△BFN中,由勾股定理得:BN===5.
23.(10分)【三角形中位线定理】
已知:在△ABC中,点D,E分别是边AB,AC的中点.直接写出DE和BC的关系;
【应用】
如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,若BC=5,CD=3,EF=2,∠AFE=45°,求∠ADC的度数;
【拓展】
如图,在四边形ABCD中,AC与BD相交于点E,点M,N分别为AD,BC的中点,MN分别交AC,BD于点F,G,EF=EG.
求证:BD=AC.
【答案】【三角形中位线定理】见解析;
【应用】135°;
【拓展】见解析.
【解答】解:【三角形中位线定理】DE∥BC,DE=BC;
理由:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC;
【应用】连接BD,如图所示,
∵E、F分别是边AB、AD的中点,
∴EF∥BD,BD=2EF=4,
∴∠ADB=∠AFE=45°,
∵BC=5,CD=3,
∴BD2+CD2=25,BC2=25,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=135°;
【拓展】证明:取DC的中点H,连接MH、NH.
∵M、H分别是AD、DC的中点,
∴MH是△ADC的中位线,
∴MH∥AC且MH=AC(三角形的中位线平行于第三边并且等于第三边的一半),
同理可得NH∥BD且NH=BD.
∵EF=EG,
∴∠EFG=∠EGF,
∵MH∥AC,NH∥BD,
∴∠EFG=∠HMN,∠EGF=∠HNM,
∴∠HMN=∠HNM,
∴MH=NH,
∴AC=BD.
24.(10分)新华书店决定用不多于28000元购进甲乙两种图书共1200本进行销售,已知甲种图书进价是乙种图书每本进价的1.4倍,若用1680元购进甲种图书的数量比用1400元购进的乙种图书的数量少10本.
(1)甲乙两种图书的进价分别为每本多少元?
(2)新华书店决定甲种图书售价为每本40元,乙种图书售价每本30元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完)
【答案】(1)甲种图书进阶每本28元,乙种图书进阶每本20元;
(2)书店甲种图书进货500本,乙种图书进货700本时利润最大,最大利润是13000元.
【解答】解:(1)设乙种图书进阶每本x元,则甲种图书进阶为每本1.4x元,
由题意得:﹣=10,
解得:x=20,
经检验,x=20是原方程的解,且符合题意,
则1.4x=1.4×20=28,
答:甲种图书进阶每本28元,乙种图书进阶每本20元;
(2)设书店甲种图书进货a本,总利润为w元,
由题意得:w=(40﹣28)a+(30﹣20)(1200﹣a)=2a+12000,
∵28a+20×(1200﹣a)≤28000,
解得:a≤500,
∵w随a的增大而增大,
∴当a最大时w最大,
∴当a=500时,w最大=2×500+12000=13000(元),
此时,乙种图书进货本数为1200﹣500=700(本)
答:书店甲种图书进货500本,乙种图书进货700本时利润最大,最大利润是13000元.
25.(10分)阅读材料:要将多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,再把它的后两项分成一组,从而得到:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n),这时a(m+n)+b(m+n)中又有公因式(m+n),于是可以提出(m+n),从而得到(m+n)(a+b),因此有am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.请回答下列问题:
(1)尝试填空:2x﹣18+xy﹣9y= ;
(2)解决问题:因式分解;ac﹣bc+a2﹣b2.
(3)拓展应用:已知三角形的三边长分别是a,b,c,且满足a2﹣2ab+2b2﹣2bc+c2=0,试判断这个三角形的形状,并说明理由.
【答案】(1)(y+2)(x﹣9);
(2)(a﹣b)(a+b+c);
(3)这个三角形是等边三角形,理由见解析.
【解答】解:(1)2x﹣18+xy﹣9y,
=(2x﹣18)+(xy﹣9y),
=2(x﹣9)+y(x﹣9),
=(y+2)(x﹣9),
故答案为:(y+2)(x﹣9);
(2)ac﹣bc+a2﹣b2
=c(a﹣b)+(a+b)(a﹣b),
=(a﹣b)(a+b+c),
(3)这个三角形是等边三角形,理由如下:
a2﹣2ab+2b2﹣2bc+c2=0,
a2﹣2ab+b2+b2﹣2bc+c2=0,
(a﹣b)2+(b﹣c)2=0,
∵(a﹣b)2≥0,(b﹣c)2≥0,
∴(a﹣b)2=0,(b﹣c)2=0,
∴a=b,b=c,
∴a=b=c,
∴这个三角形是等边三角形.
26.(10分)在△ABC中,AB=AC,∠BAC=90°,点D在边BC上.
(1)如图1,将线段AD绕着点A顺时针旋转90°,得到线段AE,连接EB,判断线段EB,BD,AD的数量关系,并证明;
(2)在图2中,在线段BD取一点F,使得DF=DC,以BF为斜边向△ABC外作等腰直角三角形BGF,连接AG.
①补全图形;
②判断线段AG与AD的数量关系,并证明.
【答案】(1)BE2+BD2=2AD2,理由见解析;
(2)①补全图形见解析;
②AG=AD,证明见解析.
【解答】解:(1)EB2+BD2=2AD2,理由如下:
∵AB=AC,∠BAC=90°,
∴∠ABC=∠C=45°,
由旋转的性质得:AE=AD,∠EAD=∠BAC=90°,
∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,
即∠EAB=∠DAC,
在△EAB与△DAC中,
,
∴△EAB≌△DAC(SAS),
∴BE=CD,∠EBA=∠C=45°,
∴∠EBC=∠EBA+∠ABC=45°+45°=90°,
在Rt△BED中,由勾股定理得:EB2+BD2=DE2,
∵AE=AD,∠EAD=90°,
∴DE2=2AD2,
∴EB2+BD2=2AD2;
(2)①补全图形,如图2;
②线段AG与AD的数量关系为:AG=AD,证明如下:
如图3,延长GF交AC于点H,连接DH、DG,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠C=45°,
∵△BGF是以BF为斜边的等腰直角三角形,
∴BG=FG,∠GBF=∠BFG=45°,∠BGF=90°,
∴∠ABG=∠ABC+∠GBF=45°+45°=90°,
∴∠BAH=∠ABG=∠BGH=90°,
∴四边形ABGH是矩形,
∴∠AHG=90°,BG=AH=FG,
∵∠HFC=∠BFG=45°,
∴∠HFC=∠C=45°,
∴△CHF是等腰直角三角形,
∵DF=DC,
∴DF=DH=DC,∠HDF=∠HDC=90°,∠DHC=∠FHD=45°,
∴∠AHD=∠AHG+∠FHD=90°+45°=135°,
∵∠GFD=180°﹣∠BFG=180°﹣45°=135°,
∴∠AHD=∠GFD,
在△AHD和△GFD中,
,
∴△AHD≌△GFD(SAS),
∴AD=DG,∠ADH=∠GDF,
∴∠ADH+∠ADB=∠GDF+∠ADB,
即∠HDF=∠ADG=90°,
∴△ADG是等腰直角三角形,
∴AG=AD.
2024年四川省成都市金堂县金龙中学中考数学模拟试卷【含解析】: 这是一份2024年四川省成都市金堂县金龙中学中考数学模拟试卷【含解析】,共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省金堂县金龙中学北师版八下数学期末数学模拟试卷 (含解析): 这是一份四川省金堂县金龙中学北师版八下数学期末数学模拟试卷 (含解析),共25页。
金堂县金龙中学八下数学综合适应性试题解析版: 这是一份金堂县金龙中学八下数学综合适应性试题解析版,共9页。












