专题八：数学广角——搭配（二）（复习课件）-三年级数学下学期期末核心考点集训（人教版）

这是一份专题八：数学广角——搭配（二）（复习课件）-三年级数学下学期期末核心考点集训（人教版），共24页。PPT课件主要包含了单元知识框架，简单的排列问题，排列与事物的顺序有关，搭配问题，简单的搭配问题，稍复杂的组合问题，组合与事物的顺序无关，简单排列问题，知识梳理，典型例题等内容，欢迎下载使用。

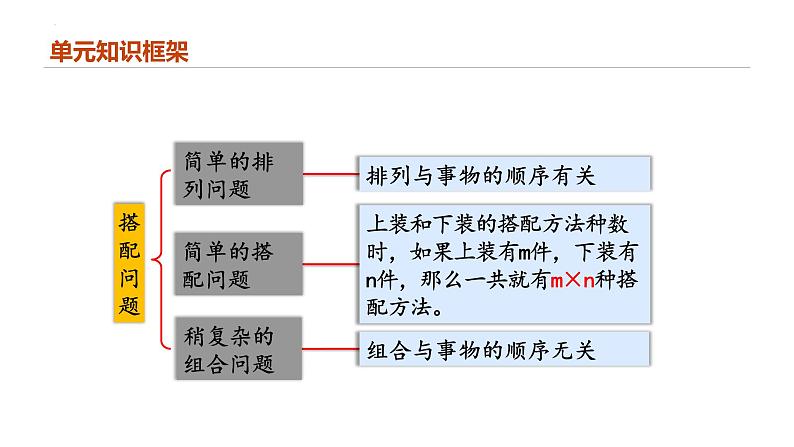
上装和下装的搭配方法种数时，如果上装有m件，下装有n件，那么一共就有m×n种搭配方法。
以组数问题为例，要做到不重复、不遗漏，可以用列举的方法，先考虑高位，再考虑低位，有顺序地依次排列，一一列举出所有的情况。注意：0在组数时，不能在首位。
例1 用 三张数字卡片能摆出多少个不同的三位数？
思路分析：可以用列举法，先摆出百位，再摆出十位和个位，但要注意0不能作百位。 用8作百位，则有860、806两种摆法；用6作百位，则有680、608两种摆法，所以共能摆出4个不同的三位数。
规范作答：能摆出4个不同的三位数，860、806、680、608。
填空：用0、1、2可以组成（ ）个没有重复数字的三位数。
错误答案：6正确答案：错点警示：
此题错在忽略了“0”不能放在首位。
规避策略：用数字组数时，不要忘记“0”不能放在首位。
知识点2：简单的搭配问题
搭配时，可以从不同的角度考虑，比如先固定一个，再按顺序一一去搭配另一个。
求上装和下装的搭配方法种数时，如果上装有m件，下装有n件，那么一共就有m×n种搭配方法。
解决简单的搭配问题，可以用图形、符号、字母等表示实物，再用连线表示不同的搭配方法。
选择：如果一种汉堡搭配一种饮料，一共有（ ）种不同的搭配方法。
错误答案：2正确答案：
规避策略：在搭配过程中要做到不重复、不遗漏，搭配有序，思考全面。
此题错在搭配时有遗漏，没有按照一定的顺序进行搭配。一共有4 种搭配方法：
下面的早餐有（ ）种不同的搭配。
饮料和点心只能各选1种。
知识点3：稍复杂的组合问题
组合中不考虑事物的先后顺序，只需注意事物的不同元素。
解决稍复杂的组合问题时，可以借助图片连线的方法来完成。
例1 8名乒乓球运动员参加单打比赛，两两配对进行淘汰赛，要决出冠军，一共要比赛多少场？
思路分析：组合与事物的顺序无关。8名乒乓球运动员要决出冠军，其比赛场次的统计可按比赛程序进行，通常淘汰赛按下图进行。
规范解答：4＋2＋1＝7（场）答：一共要比赛7场。
2.如下图，从甲地到乙地有2条路可走，从乙地到丙地有3条路可走，从甲地到丙地有4条路可走。从甲地到丙地共有多少种不同的走法？
2×3＋4＝10答：共有10种不同的走法。
1.填一填。（1）用5、7、9三张数字卡片,能摆成(　)个不同的两位数,它们分别是( 　　　 )。如果用0代替9,能摆成(　)个不同的两位数。（2）用3、4、5、6这四个数字,能组成(　　)个不同的两位数,分别是(　　　　　 )。
34、 35、 36、 43、 45、 46、 53、 54、 56、 63、64、 65
57、 59、 75、 79、 97、 95
2.唐僧师徒4人坐在椅子上。如果唐僧的位置不变，其他人可以任意换位置，一共有多少种坐法？
孙悟空 猪八戒 唐僧 沙和尚
3.用2、5、7、9组成没有重复数字的两位数，能组成多少个个位是单数的两位数？
能组成9个个位是单数的两位数。
4. 把5朵花送给给张老师、李老师、王老师，每人至少送1朵。有多少种送法？
第1组分法：1,1,3
第2组分法：1,2,2
把5朵花分成3份，有两种分法（1,1,3）和（1,2,2）
5.右面4个分类垃圾桶摆成一排，其中“其它垃圾”桶不能摆在最左边，这样的摆法一共有多少种？
这样的摆法一共有18种。
6.甲、乙、丙、丁4个人参加乒乓球小组赛，每2个人比赛一场，一共要比赛多少场？
7.按下面的要求，用5、0、7和6这几个数字写出没有重复数字的小数。（1）小于1而小数部分是三位的小数。（2）大于7而小数部分是三位的小数。
0.567 0.576 0.657 0.675 0.765 0.756
7.056 7.065 7.506 7.560 7.605 7.650