2025高考数学一轮知识必备练习第八章平面解析几何8.1直线的倾斜角斜率与方程

这是一份2025高考数学一轮知识必备练习第八章平面解析几何8.1直线的倾斜角斜率与方程，共3页。

2.理解直线的倾斜角和斜率的概念，经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式.
3.根据确定直线位置的几何要素，探索并掌握直线方程的几种形式（点斜式、两点式及一般式）.
必备知识 温故知新
【教材梳理】
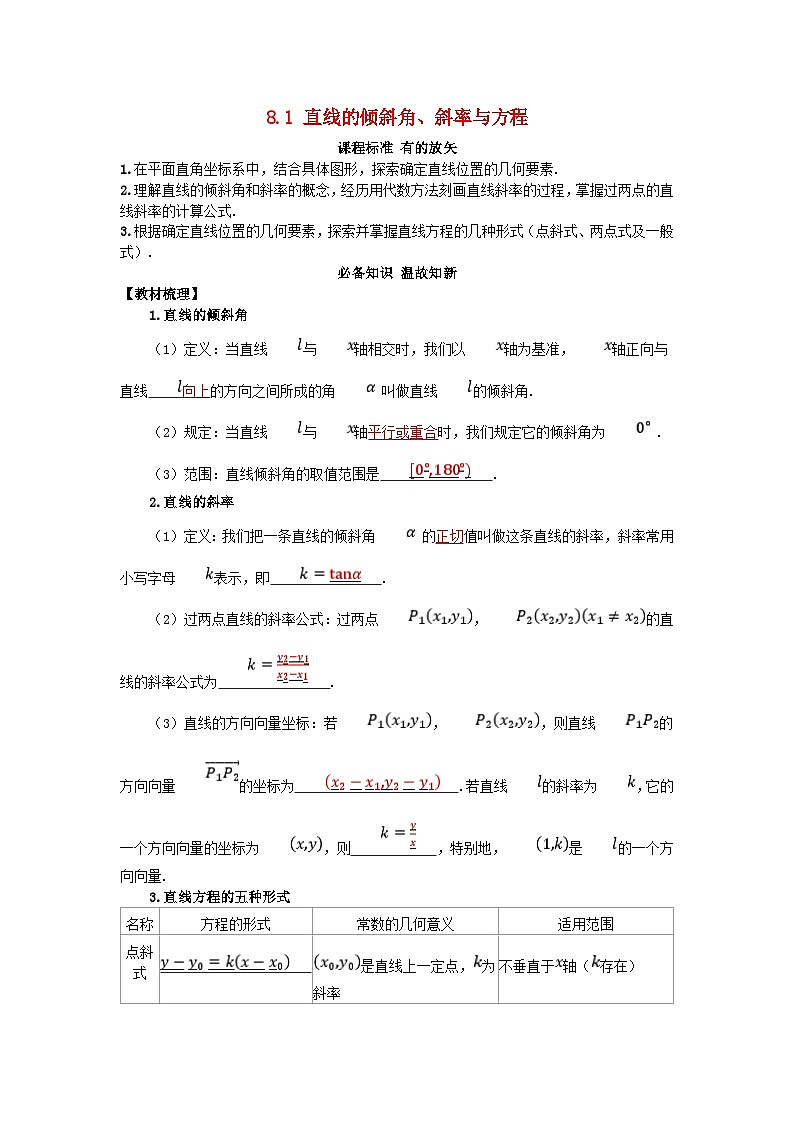
1.直线的倾斜角
（1）定义：当直线与轴相交时，我们以轴为基准，轴正向与直线向上的方向之间所成的角 叫做直线的倾斜角.
（2）规定：当直线与轴平行或重合时，我们规定它的倾斜角为 .
（3）范围：直线倾斜角的取值范围是 .
2.直线的斜率
（1）定义：我们把一条直线的倾斜角 的正切值叫做这条直线的斜率，斜率常用小写字母表示，即 .
（2）过两点直线的斜率公式：过两点，的直线的斜率公式为 .
（3）直线的方向向量坐标：若，，则直线的方向向量的坐标为 .若直线的斜率为，它的一个方向向量的坐标为，则 ，特别地，是的一个方向向量.
3.直线方程的五种形式
常用结论
1.斜率与倾斜角的对应关系
2.过点 ， 的特殊直线方程
（1）若，且，则直线垂直于轴，方程为.
（2）若，且，则直线垂直于轴，方程为.
（3）若，且，则直线即为轴，方程为.
（4）若，且，则直线即为轴，方程为.
自主评价 牛刀小试
1. 判断下列命题是否正确，正确的在括号内画“√”，错误的画“×”.
（1） 倾斜角越小，斜率越小.（ × ）
（2） 不是所有的直线都有斜率.（ √ ）
（3） 过点的直线都可用方程表示.（ × ）
（4） 能用斜截式方程表示的直线都能用点斜式方程表示. （ √ ）
（5） 直线恒过定点.（ √ ）
2. 直线的倾斜角为（ C ）
A. B. C. D.
解：由题意，得,，所以 .故选.
3. 倾斜角为 ，在轴上的截距为的直线方程是（ D ）
A. B. C. D.
解：直线的斜率为，所以直线方程为,即.故选.
4. （教材题改编）如果，且，那么直线不经过（ C ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
解：由已知，得直线 在 轴上的截距，在 轴上的截距，故直线经过第一、二、四象限，不经过第三象限.故选.名称
方程的形式
常数的几何意义
适用范围
点斜式

是直线上一定点，为斜率
不垂直于轴（存在）
斜截式

为斜率，是直线的纵截距，是点斜式的特例
不垂直于轴（存在）
两点式

,是直线上两个定点
不垂直于轴和轴
截距式

为横截距，为纵截距，是两点式的特例
不垂直于轴和轴，且不过原点
一般式


,,为系数
任何位置的直线
图示
倾斜角（范围）




斜率（范围）


不存在