2024年江苏省南京市鼓楼区南京民办求真中学九年级中考数学三模试题(无答案)

这是一份2024年江苏省南京市鼓楼区南京民办求真中学九年级中考数学三模试题(无答案)，共8页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

一、选择题（本大题共6小题，每小题2分，共12分）
1．为了了解某县初中4500名七年级学生的身高情况，从该县各初中学校七年级中随机抽取800名学生进行测量．关于这个问题，下列说法不正确的是（ ）
A．4500名七年级学生的身高情况的全体是总体
B．每名学生的身高情况是个体
C．抽取的800学生的身高情况是样本
D．样本容量是4500名
2．如图，数轴上位于数字1和2之间的点表示的数为，则的取值范围是（ ）
A．B．C．D．
3．下列各组数中是勾股数的为（ ）
A．B．C．7，8，9D．
4．在中，，．当最大时，的长是（ ）
A．B．C．D．
5．已知反比例函数的图象经过点，则下列关于与的大小关系正确的是（ ）
A．B．C．D．不能确定
6．如图，在中，，，是上的一个动点，则的度数可能是（ ）
第6题
A．B．C．D．
二．填空题（本大题共10小题，每小题2分，共20分）
7．分解因式：______．
8．若关于的方程有实数根，则的取值范围是______．
9．计算的结果是______．
10．如图所示，为了验证某个机械零件的截面是个半圆，某同学用三角板放在了如下位置，通过实际操作可以得出结论，该机械零件的截面是半圆，其中蕴含的数学依据是______．
第10题
11．在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强与汽缸内气体的体积成反比例，关于的函数图象如图所示．若压强由加压到，则气体体积压缩了______．
第11题
12．如图，点是线段的黄金分割点，即，若以为边的正方形的面积为100，则长为，宽为的矩形的面积为______．
第12题
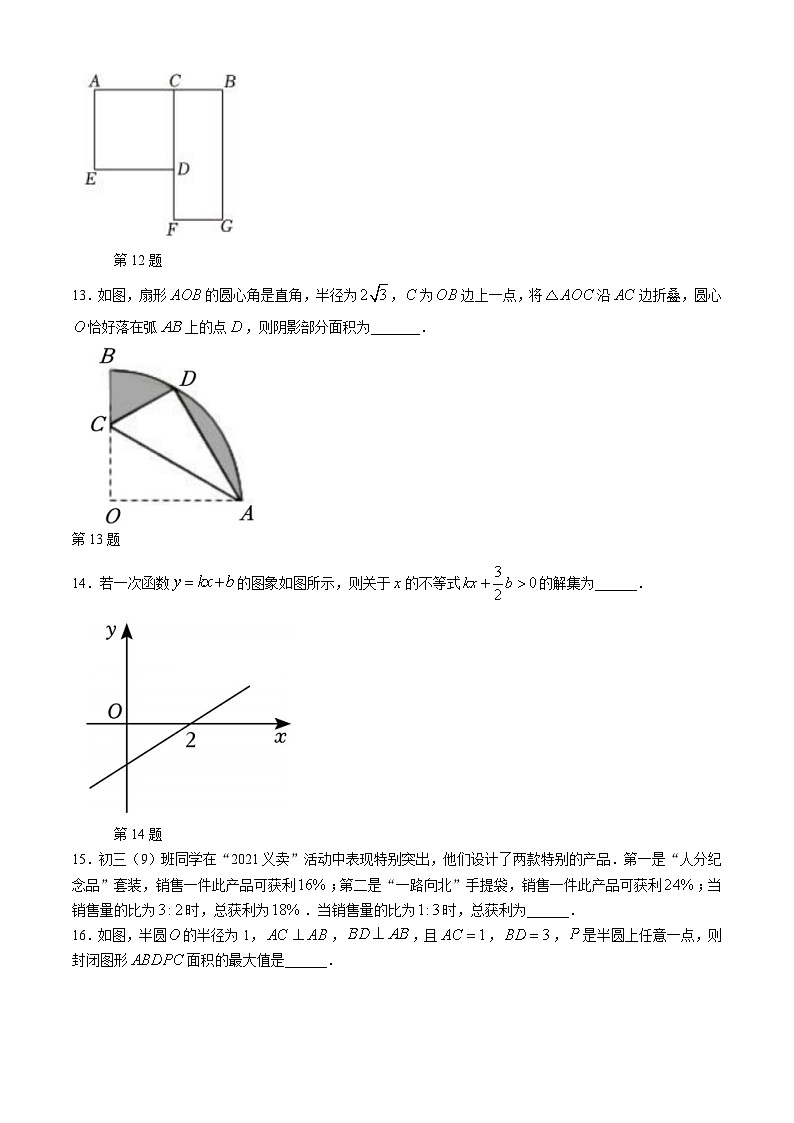
13．如图，扇形的圆心角是直角，半径为，为边上一点，将沿边折叠，圆心恰好落在弧上的点，则阴影部分面积为_______．
第13题
14．若一次函数的图象如图所示，则关于的不等式的解集为______．
第14题
15．初三（9）班同学在“2021义卖”活动中表现特别突出，他们设计了两款特别的产品．第一是“人分纪念品”套装，销售一件此产品可获利；第二是“一路向北”手提袋，销售一件此产品可获利；当销售量的比为时，总获利为．当销售量的比为时，总获利为______．
16．如图，半圆的半径为1，，，且，，是半圆上任意一点，则封闭图形面积的最大值是______．
第16题
三、解答题（本大题共11小题，共88分．解答时应写出必要的文字说明、证明过程或演算步骤）
17．（4分）（1）计算：．
18．（5分）化简：，再从中选择一个合适的数作为的值代入求值．
19．（8分）如图，在中，点分别是的中点，分别连接．
（1）求证：四边形为平行四边形；
（2）当满足什么条件时，四边形是菱形，并证明．
20．（34分）如图，是某卖场国产大米牌手机的宣传广告．
（1）你认为大米手机5月份的销售量必定是三个品牌手机中最高的吗？请说明你的理由．
（2）若各品牌手机2015年4月的销售量如下：
求该卖场5月份三个品牌手机销售量的平均增长率．
21．（25分）如图，有四张背面完全相同的纸牌，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．
（1）从中随机摸出一张，则摸出的牌面图形是中心对称图形的概率为______；
（2）小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用表示）．
22．（6分）尺规作图：如图，已知正方形，在边上求作一点，使．（保留作图痕迹，不写作法）
23．（44分）桔槔俗称“吊杆”“称杆”（如图1），是我国古代农用工具，始见于《墨子·备城门》，是一种利用杠杆原理的取水机械．如图2所示的是桔槔示意图，是垂直于水平地面的支撑杆，米，是杠杆，且米，．当点位于最高点时，．
图1 图2
（1）求点位于最高点时到地面的距离；
（2）当点从最高点逆时针旋转到达最低点时，求此时水桶上升的高度．
（参考数据：，，）
24．（9分）社区利用一块矩形空地建了一个小型停车场，其布局如图所示．已知米，米，阴影部分设计为停车位，要铺花砖，其余部分均为宽度为米的道路．已知铺花砖的面积为880平方米．
（1）求道路的宽是多少米？
（2）该停车场共有车位60个，据调查分析，当每个车位的月租金为200元时，可全部租出；若每个车位的月租金每上涨5元，就会少租出1个车位．问当每个车位的月租金上涨多少元时，停车场的月租金收入最大？
25．（10分）两个函数交点的横坐标可视为两个函数联立后方程的根，例如函数的图象与函数的图象交点的横坐标可视为方程的根．
（1）函数的图象与函数的图象有两个不同交点，求取值范围．
（2）已知二次函数（为常数）．
①设直线与抛物线有两个不同交点，求取值范围．
②已知点，若抛物线与线段只有一个公共点，请直接写出的取值范围．
26．（12分）综合与探究
我们知道：顶点在圆上，并且两边都和圆相交的角叫做圆周角，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．类似地，我们定义：顶点在圆外，并且两边都和圆相交的角叫做圆外角．
【探究】
圆外角的度数与它所夹的弧所对的圆心角的度数之间有什么关系？
【实验】
（1）如图1，当圆外角的两条边分别与有两个公共点时，改变的度数，测量得到如下数据：
猜想：______．（用含的式子表示）
图1 图2
【特例】
（2）当圆外角的其中一条边与只有一个公共点时，如图2，射线与相切于点，射线经过圆心，交于另一点，设所对的圆心角度数分别为，写出的度数与，之间的数量关系，并证明．
【应用】
（3）在（2）的条件下，连接，若，，求的半径．
27．（12分）综合与实践
背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为的三角形称为型三角形，例如：三边长分别为或的三角形就是型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．
实践操作 如图1，在矩形纸片中，，．
第一步：如图2，将图1中的矩形纸片沿过点的直线折叠，使点落在上的点处，折痕为，再沿折叠，然后把纸片展平．
第二步：如图3，将图2中的矩形纸片再次折叠，使点重合，折痕为，然后展平，隐去．
第三步：如图4，将图3中的矩形纸片沿折叠，得到，再沿折叠，折痕为，与折痕交于点，然后展平．
图1 图2 图3 图4
问题解决
（1）请在图2中证明四边形是正方形．
（2）请在图4中判断与的数量关系，并加以证明；
（3）请在图4中证明型三角形；
探索发现
（4）在不添加字母的情况下，图4中还有哪些三角形是型三角形？请找出并直接写出它们的名称．
手机品牌
芒果手机
四星手机
大米手机
销售量（台）
200
80
120
的度数
所对的圆心角度数
所对的圆心角度数