第4章《三角形》【易错题拔高卷】-2023-2024学年北师大版数学七年级下册章节复习检测卷

这是一份第4章《三角形》【易错题拔高卷】-2023-2024学年北师大版数学七年级下册章节复习检测卷，文件包含第4章《三角形》教师版docx、第4章《三角形》学生版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。
考试时间：100分钟 试卷满分：100分 难度系数：0.50
一、选择题（本大题共10小题，每小题2分，共20分．在每小题所给出的四个选项中，恰有一项是符合
题目要求的，请将正确选项前的字母代号填写在括号内）
1．（2分）（2023春•香坊区校级期中）下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（ ）
A．13，11，20B．3，7，10C．6，8，16D．3，3，7
解：A、∵13+11＞20，
∴长度为13，11，20的三根小木棒，能摆成三角形，本选项符合题意；
B、∵3+7＝10，
∴长度为3，7，10的三根小木棒，不能摆成三角形，本选项不符合题意；
C、∵6+8＜16，
∴长度为6，8，16的三根小木棒，不能摆成三角形，本选项不符合题意；
D、∵3+3＜7，
∴长度为3，3，7的三根小木棒，不能摆成三角形，本选项不符合题意；
故选：A．
2．（2分）（2023秋•淮南期中）下列各图中，作△ABC边AC上的高，正确的是（ ）
A．B．
C．D．
解：A、AD是△ABC边BC上的高，不符合题意；
B、AD是△ADC边AC上的高，不符合题意；
C、BD是△DBC边BC上的高，不符合题意；
D、BD是△ABC边AC上的高，符合题意；
故选：D．
3．（2分）（2023春•沈河区期末）用一块含45°角的透明直角三角板画已知△ABC 的边AB上的高，下列三角板的摆放位置正确的是（ ）
A．B．
C．D．
解：用一块含45°角的透明直角三角板画已知△ABC 的边AB上的高，下列三角板的摆放位置正确的是
故选：C．
4．（2分）（2023春•达川区期中）给出下列说法：
①从直线外一点到这条直线的垂线段叫做这个点到这条直线的距离；
②三角形的角平分线是射线；
③三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外；
④任何一个三角形都有三条高、三条中线、三条角平分线；
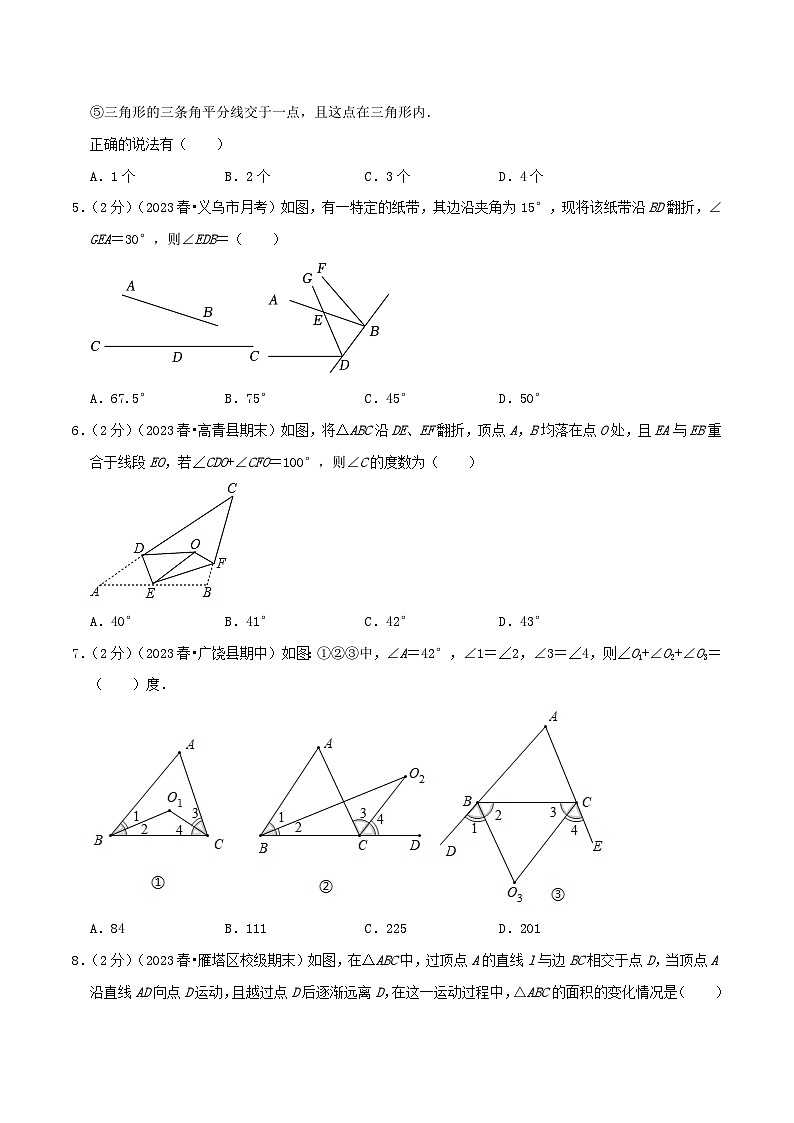
⑤三角形的三条角平分线交于一点，且这点在三角形内．
正确的说法有（ ）
A．1个B．2个C．3个D．4个
解：①从直线外一点到这条直线的垂线段的长度叫做这个点到这条直线的距离，故本小题说法错误；
②三角形的角平分线是线段，故本小题说法错误；
③三角形的高所在的直线交于一点，这一点在三角形内或在三角形外或在三角形的一边上，故本小题说法错误；
④任何一个三角形都有三条高、三条中线、三条角平分线，说法正确；
⑤三角形的三条角平分线交于一点，且这点在三角形内，说法正确；
故选：B．
5．（2分）（2023春•义乌市月考）如图，有一特定的纸带，其边沿夹角为15°，现将该纸带沿BD翻折，∠GEA＝30°，则∠EDB＝（ ）
A．67.5°B．75°C．45°D．50°
解：如图，延长CD交AB的延长线于点M，由题意可知，∠M＝15°，
∵∠AEG＝30°，
∴∠DEB＝30°，
∴∠EDM＝180°﹣∠DEB﹣∠M＝135°，
由折叠可知，∠EDB＝∠MDB，
∴∠EDB＝135°÷2＝67.5°．
故选：A．
6．（2分）（2023春•高青县期末）如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO＝100°，则∠C的度数为（ ）
A．40°B．41°C．42°D．43°
解：如图，连接AO、BO．
由题意EA＝EB＝EO，
∴∠AOB＝90°，∠OAB+∠OBA＝90°，
∵DO＝DA，FO＝FB，
∴∠DAO＝∠DOA，∠FOB＝∠FBO，
∴∠CDO＝2∠DAO，∠CFO＝2∠FBO，
∵∠CDO+∠CFO＝100°，
∴2∠DAO+2∠FBO＝100°，
∴∠DAO+∠FBO＝50°，
∴∠CAB+∠CBA＝∠DAO+∠OAB+∠OBA+∠FBO＝140°，
∴∠C＝180°﹣（∠CAB+∠CBA）＝180°﹣140°＝40°，
故选：A．
7．（2分）（2023春•广饶县期中）如图：①②③中，∠A＝42°，∠1＝∠2，∠3＝∠4，则∠O1+∠O2+∠O3＝（ ）度．
A．84B．111C．225D．201
解：∵①②③中，∠A＝42°，∠1＝∠2，∠3＝∠4，
∴①中，∠2+∠4＝（∠1+∠2+∠3+∠4）＝（180°﹣42°）＝69°，故∠O1＝180°﹣69°＝111°；
②中，∠O2＝∠4﹣∠2＝[（∠3+∠4）﹣（∠1+∠2）]＝∠A＝21°；
③中，∠ABC+∠ACB＝180°﹣∠A＝180°﹣42°＝138°，则∠1+∠2+∠3+∠4＝180°+180°﹣138°＝222°
故∠O3＝180°﹣（∠2+∠3）＝180°﹣×222°＝69°
∴∠O1+∠O2+∠O3＝111°+21°+69°＝201°
故选：D．
8．（2分）（2023春•雁塔区校级期末）如图，在△ABC中，过顶点A的直线l与边BC相交于点D，当顶点A沿直线AD向点D运动，且越过点D后逐渐远离D，在这一运动过程中，△ABC的面积的变化情况是（ ）
A．由大变小
B．由小变大
C．先由大变小，后由小变大
D．先由小变大，后由大变小
解：设点A到BC的距离为h，
∴△ABC的面积＝BC•h，
由题意得：
在A点的运动过程中，BC的长度不变，点A到BC的距离h先变小，然后变大，
∴△ABC的面积的变化情况是先由大变小，后由小变大，
故选：C．
9．（2分）（2023春•钟楼区校级期中）如图，△ABC的两条中线AD、BE交于点F，若四边形CDFE的面积为17，则△ABC的面积是（ ）
A．54B．51C．42D．41
解：如图所示，连接CF，
∵△ABC的两条中线AD、BE交于点F，
∴S△BCE＝S△ABD，
∴S四边形CDFE＝S△ABF＝17，
∵BE是△ABC的中线，FE是△ACF的中线，
∴S△BCE＝S△ABE，S△FCE＝S△FAE，
∴S△BCF＝S△BAF＝17，
同理可得，S△ACF＝S△BAF＝17，
∴S△BCF＝S△BAF＝S△ACF＝17，
∴S△ABC＝3S△BAF＝3×17＝51，
故选：B．
10．（2分）（2023秋•江门期末）如图，在Rt△ABC中，∠ABC＝90°，以AC为边，作△ACD，满足AD＝AC，E为BC上一点，连接AE，2∠BAE＝∠CAD，连接DE，下列结论中正确的有（ ）
①AC⊥DE；②∠ADE＝∠ACB；③若CD∥AB，则AE⊥AD；④DE＝CE+2BE．
A．①②③B．②③④C．②③D．①②④
解：如图，延长EB至G，使BE＝BG，设AC与DE交于点M，
∵∠ABC＝90°，
∴AB⊥GE，
∴AB垂直平分GE，
∴AG＝AE，∠GAB＝∠BAE＝∠DAC，
∵∠BAE＝∠GAE，
∴∠GAE＝∠CAD，
∴∠GAE+∠EAC＝∠CAD+∠EAC，
∴∠GAC＝∠EAD，
在△GAC与△EAD中，
，
∴△GAC≌△EAD（SAS），
∴∠G＝∠AED，∠ACB＝∠ADE，
∴②是正确的；
∵AG＝AE，
∴∠G＝∠AEG＝∠AED，
∴AE平分∠BED，
当∠BAE＝∠EAC时，∠AME＝∠ABE＝90°，则AC⊥DE，
当∠BAE≠∠EAC时，∠AME≠∠ABE，则无法说明AC⊥DE，
∴①是不正确的；
设∠BAE＝x，则∠CAD＝2x，
∴∠ACD＝∠ADC＝＝90°﹣x，
∵AB∥CD，
∴∠BAC＝∠ACD＝90°﹣x，
∴∠CAE＝∠BAC﹣∠EAB＝90°﹣x﹣x＝90°﹣2x，
∴∠DAE＝∠CAE+∠DAC＝90°﹣2x+2x＝90°，
∴AE⊥AD，
∴③是正确的；
∵△GAC≌△EAD，
∴CG＝DE，
∵CG＝CE+GE＝CE+2BE，
∴DE＝CE+2BE，
∴④是正确的，
故选：B．
二、填空题（本大题共10小题，每题2分，共20分．不需写出解答过程，请将正确答案填写在横线上）
11．（2分）（2023春•山亭区期中）如图为6个边长相等的正方形的组合图形，则∠1+∠3﹣∠2＝ 45° ．
解：如图：
在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠1＝∠4，
∵∠3+∠4＝90°，
∴∠1+∠3＝90°，
又∵∠2＝45°，
∴∠1+∠3﹣∠2＝90°﹣45°＝45°．
故答案为：45°．
12．（2分）（2023春•宛城区期末）如图，AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝50°，点F为边AB上一点，当△BDF为直角三角形时，则∠ADF的度数为 20°或60° ．
解：如图所示，当∠BFD＝90°时，
∵AD是△ABC的角平分线，∠BAC＝60°，
∴∠BAD＝30°，
∴Rt△ADF中，∠ADF＝60°；
如图，当∠BDF＝90°时，
同理可得∠BAD＝30°，
∵CE是△ABC的高，∠BCE＝50°，
∴∠BFD＝∠BCE＝50°，
∴∠ADF＝∠BFD﹣∠BAD＝20°，
综上所述，∠ADF的度数为20°或60°．
故答案为：20°或60°．
13．（2分）（2023春•仪征市期末）如图，DE⊥AB垂足为E，交AC于点F，∠A＝45°，∠D＝25°，则∠ACB＝ 70° ．
解：∵DE⊥AB，
∴∠DEB＝90°，
∵∠D＝25°，
∴∠B＝90°﹣∠D＝65°，
∵∠A＝45°，
∴∠ACB＝180°﹣∠A﹣∠ABC＝70°，
故答案为：70°．
14．（2分）（2022秋•石门县期末）如果一个三角形的三个内角的度数之比为1：2：3，那么这个三角形中最大的一个内角等于 90 度．
解：设三个内角的度数分别为k，2k，3k．
则k+2k+3k＝180°，
解得k＝30°，
则2k＝60°，3k＝90°，
这个三角形最大的角等于90°．
故答案为：90．
15．（2分）（2022春•泰兴市期末）如图，△ABC的顶点A、B、C都在小正方形的顶点上，我们把这样的三角形叫做格点三角形．则图中与△ABC有唯一公共顶点C且与△ABC全等的格点三角形共有 20 个（不包括△ABC）．
解：如图：
与△ABC有唯一公共顶点C且与△ABC全等的格点三角形有：
△CEB，△CEB1，△CA1B1，△CA1B2，△CE1B2，△CE1B3，△CA2B3，△CA2B4，△CE2B4，△CE2B5，△CA3B5，△CA3B6，△CB6E3，△CE3B7，△CA1E3，△CA1E2，△CA2E，△CA2E3，△CA3E1，△CA3E，
共有20个，
故答案为：20．
16．（2分）（2023秋•伊犁州期末）已知：如图所示，在△ABC中，点D，E，F分别为BC，AD，CE的中点，且S△ABC＝4cm2，则阴影部分的面积为 1 cm2．
解：∵D为BC中点，根据同底等高的三角形面积相等，
∴S△ABD＝S△ACD＝S△ABC＝×4＝2（cm2），
同理S△BDE＝S△CDE＝S△BCE＝×2＝1（cm2），
∴S△BCE＝2（cm2），
∵F为EC中点，
∴S△BEF＝S△BCE＝×2＝1（cm2）．
故答案为1．
17．（2分）（2023春•金牛区校级期中）△ABC中，∠A＝90°．现进行第一次操作：如图1作射线BA1，使得∠ABA1＝∠ABC，作射线CA1，使得∠ACA1＝∠ACD．再进行第二次操作：如图2作射线BA2，使得∠A1BA2＝∠A1BC，作射线CA2，使得∠A1CA2＝∠A1CD．再进行第三次操作：如图3作射线BA3使得∠A2BA3＝∠A2BC，作射线CA3，使得∠A2CA3＝∠A2CD．则∠A3＝ 20° ．
解：第一次操作：
∵∠A＝90°，
∴∠ABC+∠ACB＝90°，
∵∠ABA1＝∠ABC，∠ACA1＝∠ACD，
∴∠DCA1＝（90°+∠ABC）＝45°+，∠CBA1＝∠ABC，
第二次操作：
∵∠A1BA2＝∠A1BC，∠A1CA2＝∠A1CD，
∴A2BC＝∠A1BC＝∠ACB，∠A2CD＝∠A1CD＝（90°﹣∠ABC）＝60°﹣∠ABC，
第三次操作：
∵∠A2BA3＝∠A2BC，∠A2CA3＝∠A2CD，
∴∠A3BC＝∠ACB，∠A3CD＝40°﹣∠ABC，
∴∠A3＝∠A3CD﹣∠A3BC＝40°﹣∠ABC﹣∠ACB＝40°﹣（∠ABC+∠ACB）＝20°；
故答案为：20°．
18．（2分）（2023春•思明区校级期末）如图，点D和点E是△ABC中AB和AC边上的两点，将∠A沿DE翻折，使点A的对应点A′恰好落在射线BC上，A′D与EC相交于点F，若∠BDA′＝∠CEA′+2∠DA′B，∠B+∠DFC＝160°，则∠EDF的度数为 40° ．
解：由翻折可得：∠ADE＝∠EDA′，∠A＝∠DA′E，∠AED＝∠A′ED．
设∠A＝∠DA′E＝α，∠ADE＝∠EDA′＝β，
∴∠B＝∠ADA′﹣∠DA′B＝2β﹣∠DA′B，
∠DFC＝∠A+∠ADF＝2β+α，
∴∠B+∠DFC＝4β+α﹣∠DA′B，
∵∠B+∠DFC＝160°，
∴4β+α﹣∠DA′B＝160°，
∵∠BDA′＝∠CEA′+2∠DA′B，
∴180°﹣∠ADA′＝∠CEA′+2∠DA′B，
∴180°﹣2β＝∠CEA′+2∠DA′B，
∴∠CEA′+2∠DA′B+2β＝180°，
∵∠AED＝180°﹣β﹣α＝∠DEA′＝∠DEC+∠CEA′，
∠DEC＝∠A+∠ADE＝α+β，
∴180°﹣β﹣α＝α+β+∠CEA′，
∴2α+2β+∠CEA′＝180°，
∴∠CEA′+2∠DA′B+2β＝2α+2β+∠CEA′，
∴∠DA′B＝α，
∵4β+α﹣∠DA′B＝160°，
∴4β+α﹣α＝160°，
∴β＝40°，
∴∠EDF＝40°．
故答案为：40°．
19．（2分）（2023春•常州期末）将一副三角尺按如图所示放置，直角顶点重合于点C，∠B＝60°，∠E＝45°，斜边AB⊥DE，垂足为F，则∠ACD＝ 15° ．
解：∵∠ACB＝90°，∠B＝60°，
∴∠A＝90°﹣∠B＝30°，
∵DE⊥AB，
∴∠AFM＝90°，
∴∠AMF＝90°﹣∠A＝60°，
∴∠AMF＝∠CME＝60°，
∵∠E＝45°，
∴∠MCE＝180°﹣∠E﹣∠CME＝75°，
∵∠DCE＝90°，
∴∠ACD＝∠DCE﹣∠MCE＝15°，
故答案为：15°．
20．（2分）（2022•盘龙区二模）如图，已知四边形ABCD中，AB＝10cm，BC＝8cm，CD＝12cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3cm/s的速度沿B﹣C﹣B运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 或3或或 cm/s时，能够使△BPE与△CQP全等．
解：设点P在线段BC上运动的时间为t s，
①点P由B向C运动时，BP＝3t（cm），CP＝（8﹣3t）cm，
∵△BPE≌△CQP，
∴BE＝CP＝5，
∴5＝8﹣3t，
解得t＝1，
∴BP＝CQ＝3，
此时，点Q的运动速度为3÷1＝3（cm/s）；
②点P由B向C运动时，
∵△BPE≌△CPQ，
∴BP＝CP，
∴3t＝8﹣3t，
t＝，
此时，点Q的运动速度为：5÷＝（cm/s）；
③点P由C向B运动时，CP＝3t﹣8，
∵△BPE≌△CQP，
∴BE＝CP＝5，
∴5＝3t﹣8，
解得t＝，
∴BP＝CQ＝3，
此时，点Q的运动速度为3÷＝（cm/s）；
④点P由C向B运动时，
∵△BPE≌△CPQ，
∴BP＝CP＝4，
3t﹣8＝4，
t＝4，
∵BE＝CQ＝5，
此时，点Q的运动速度为5÷4＝（cm/s）；
综上所述：点Q的运动速度为cm/s或3cm/s或cm/s或cm/s；
故答案为：或3或或．
三、解答题（本大题共8小题，共60分．解答时应写出文字说明、证明过程或演算步骤）
21．（6分）（2023秋•互助县期末）如图，在△ABC中，∠ABC＝50°，CE为AB边上的高，AF与CE交于点G．若∠AFC＝80°，求∠AGC的度数．
解：∵CE是AB边上的高，
∴∠BEC＝90°，
在△ABC中，∠ABC＝50°，
∴∠BCE＝180°﹣∠ABC﹣∠BEC＝40°，
∵∠AFC＝80°，
∴∠CGF＝180°﹣∠AFC﹣∠BCE＝60°，
∴∠AGC＝180°﹣∠CGF＝120°．
22．（6分）（2023春•二道区校级期末）如图，在直角三角形ABC中，CD是斜边AB上的高，∠BCD＝35°，求：
（1）∠FBC的度数．
（2）∠A的度数．
对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
解：（1）∵CD⊥AB（ CD是斜边AB上的高 ）
∴∠CDB＝ 90° ．
∵∠EBC＝∠CDB+∠BCD（ 三角形的外角的性质 ）
∴∠EBC＝ 90° +35°＝ 125° （等量代换）
（2）∵∠EBC＝∠A+∠ACB
∴∠A＝∠EBC﹣∠ACB（等式的性质）
∵∠ACB＝90°（已知）
∴∠A＝ 125° ﹣90°＝ 35° （等量代换）．
解：（1）∵CD⊥AB（CD是斜边AB上的高），
∴∠CDB＝90°．
∵∠EBC＝∠CDB+∠BCD（三角形的外角的性质），
∴∠EBC＝90°+35°＝125°（等量代换）．
故答案为：CD是斜边AB上的高；90°；三角形的外角的性质；90°；125°．
（2）∵∠EBC＝∠A+∠ACB
∴∠A＝∠EBC﹣∠ACB（等式的性质），
∵∠ACB＝90°（已知），
∴∠A＝125°﹣90°＝35°（等量代换）．
故答案为：125°；35°．
23．（8分）（2023春•石狮市校级期中）如图，在△ABC中，∠ABC＝65°，∠C＝35°，AD是△ABC的角平分线．
（1）求∠ADC的度数．
（2）过点B作BE⊥AD于点E，BE延长线交AC于点F．求∠AFE的度数．
解：（1）∵∠ABC＝65°，∠C＝35°，
∴∠BAC＝80°，
又∵AD是△ABC的角平分线，
∴∠DAF＝∠BAC＝40°，
∴△ACD中，∠ADC＝180°﹣40°﹣35°＝105°；
（2）∵BE⊥AD，
∴∠AEF＝90°，
由（1）可得∠EAF＝40°，
∴∠AFE＝180°﹣40°﹣90°＝50°．
24．（8分）（2023春•福田区校级期中）如图1，把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上．
（1）填空：∠1＝ 120 °，∠2＝ 90 °．
（2）如图2，现将三角板绕点B点逆时针旋转n°，当0＜n＜90，且点C恰好落在DG边上时，
①请直接写出∠1＝ （120﹣n） °，∠2＝ 90+n °．（结果用含n的代数式表示）；
②若∠2恰好是∠1的倍，求n的值．
（3）如图1三角板ABC的放置，现将AB绕点A以每秒1°的转速逆时针旋转，同时CF绕点C以每秒2°的转速顺时针旋转，当CF第一次旋转回到起点时，CF、AB均停止转动，设旋转时间为t（s）．请求出当t为何值时，AB∥CF．
解：（1）由图1可知：∠1＝180°﹣60°＝120°，∠2＝∠ACF＝90°．
故答案为：120，90．
（2）①如图2，∵DG∥EF，
∴∠DCB＝∠CBF＝n°，
∴∠ACD＝90°﹣n°，
∴∠1＝∠A+∠ACD＝（120﹣n）°，
∵DG∥EF，
∴∠BCG＝180°﹣∠CBF＝180°﹣n°，
∵∠ACB+∠BCG+∠2＝360°，
∴∠2＝360°﹣∠ACB﹣∠BCG
＝360°﹣90°﹣（180°﹣n°）
＝（90+n）°．
故答案为：（120﹣n），（90+n）．
②当 时，
，
解得n＝30．
∴n的值是30．
答：n的值是30．
（3）分类如下：
①0＜t＜90，如图：
由题意，得∠ACF'＝（90+2t）°，∠CAB'＝（t﹣30）°，
∵AB'∥CF'，
∴∠ACF'+∠CAB'＝180°，
即（90+2t）°+（t﹣30）°＝180°，
解得t＝40．
②90≤t＜120，如图：
由题意，得∠ACF'＝（270﹣2t）°，∠CAB'＝（t﹣30）°，
∵AB'∥CF'，
∴∠ACF'＝∠CAB'，
即（270﹣2t）°＝（t﹣30）°
解得t＝100．
③120≤t＜180，如图：
由题意，得∠F'CA＝（2t﹣270）°，∠CAB'＝（t﹣30）°，
∵AB'∥CF'，
∴∠F'CA+∠CAB'＝180°，
即（2t﹣270）°+（t﹣30）°＝180°，
解得t＝160．
综上所述，当t＝40，100，160时，AB∥CF．
25．（8分）（2023秋•大观区校级期中）如图，在△ABC中，点D在AB上，过点D作DE∥BC，交AC于点E，DP平分∠ADE，交∠ACB的平分线于点P，CP与DE相交于点G，∠ACF的平分线CQ与DP相交于点Q．
（1）若∠A＝50°，∠B＝60°，则∠DPC＝ 115 °，∠Q 25 °；
（2）若∠A＝50°，当∠B的度数发生变化时，∠DPC、∠Q的度数是否发生变化？并说明理由；
（3）若△PCQ中存在一个内角等于另一个内角的三倍，请直接写出所有符合条件的∠A的度数 45°或60°或120°或135° ．
解：（1）∵∠A＝50°，∠B＝60°，
∴∠ACB＝70°，
∴∠BCP＝∠ACB＝35°，
∵DE∥BC，
∴∠ADE＝∠B＝60°，∠PGD＝∠PCB＝35°，
∵∠PDE＝∠ADE＝30°，
∴∠DPC＝180°﹣∠PDE﹣∠PGD＝115°；
又∵∠ACQ＝∠ACF，
∴∠PCQ＝∠ACQ+∠ACP＝（∠ACF+∠ACB）＝90°，
∴∠Q＝∠DPC﹣∠QCP＝25°；
故答案为：115，25；
（2）∠DPC、∠Q的度数不会发生变化．
理由：由（1）得：∵∠PDE＝∠ADE＝∠B，∠PGD＝∠BCP＝∠ACB，
∴∠DPC＝180°﹣∠PDE﹣∠PGD＝180°﹣∠B﹣∠ACB＝180°﹣（∠B+∠ACB）＝180°﹣（180°﹣∠A）＝90°+∠A＝115°；
∴∠Q＝∠DPC﹣∠QCP＝25°；
（3）设∠A＝x，则，
∵CP平分∠ACB，CQ平分∠ACF，
∴，，
∴，，
因为△PCQ中存在一个内角等于另一个内角的三倍，
∴①当∠Q＝3∠QPC时，，
∴x＝135°，
②当∠QPC＝3∠Q时，，
∴x＝45°，
③当∠PCQ＝3∠Q时，，
∴x＝60°，
④当∠PCQ＝3∠QPC时，，
∴x＝120°，
综上①②③④可知∠A＝45°或60°或120°或135°．
故答案为：45°或60°或120°或135°．
26．（8分）（2022秋•淮南期末）（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC+∠ACB＝ 150° ，∠XBC+∠XCB＝ 90° ．
（2）如图2，△ABC的位置不变，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C，那么∠ABX+∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小．
解：（1）∵∠A＝30°，
∴∠ABC+∠ACB＝150°，
∵∠X＝90°，
∴∠XBC+∠XCB＝90°，
故答案为：150°；90°．
（2）不变化．
∵∠A＝30°，
∴∠ABC+∠ACB＝150°，
∵∠X＝90°，
∴∠XBC+∠XCB＝90°，
∴∠ABX+∠ACX＝（∠ABC﹣∠XBC）+（∠ACB﹣∠XCB）
＝（∠ABC+∠ACB）﹣（∠XBC+∠XCB）
＝150°﹣90°
＝60°．
27．（8分）（2023春•虹口区校级期末）（此题不需要写出括号内的定理理由）
（1）如图①，四边形ABCD，∠ABC与∠ADC互补，BC＝CD，点E、F在线段AB、AD上且BE+DF＝EF，若∠A＝n°，求：∠ECF的度数；
（2）如图②，若点E、F在线段AB、AD的延长线上，其余条件均不变，求∠ECF的度数．
解：（1）延长AD到G，使DG＝BE，
∵∠ABC+∠ADC＝180°，
∴∠A+∠BCD＝360°﹣（∠ABC+∠ADC）＝180°，
∵∠ADC+∠CDG＝180°，
∴∠CDG＝∠ABC，
∵BC＝CD，
∴△CBE≌△CDG（SAS），
∴CE＝CG，∠BCE＝∠DCG，
∵BE+DF＝EF，DG+DF＝FG，
∴EF＝FG，
∵CF＝CF，
∴△CEF≌△CGF（SSS），
∴∠ECF＝∠GCF，
∴∠ECF＝∠GCD+∠DCF＝∠BCE+∠DCF＝∠BCD＝（180°﹣∠A）＝（180°﹣n°）＝90°﹣n°，
∴∠ECF的度数为90°﹣n°；
（2）延长DA到G，使DG＝BE，
∵∠ABC+∠ADC＝180°，∠ABC+∠CBE＝180°，
∴∠ADC＝∠CBE，
∵BC＝CD，
∴△CBE≌△CDG（SAS），
∴CE＝CG，∠BEC＝∠G，
∵BE+DF＝EF，DG+DF＝FG，
∴EF＝FG，
∵CF＝CF，
∴△CEF≌△CGF（SSS），
∴∠G＝∠CEF，∠CFE＝∠CFG＝∠AFE，
∴∠BEC＝∠CEF＝∠AEF，
∴∠ECF＝180°﹣（∠CEF+∠CFE）
＝180°﹣（∠AEF+∠AFE）
＝180°﹣（∠AEF+∠AFE）
＝180°﹣（180°﹣∠EAF）
＝180°﹣（180°﹣n°）
＝180°﹣90°+n°
＝90°+n°，
∴∠ECF的度数为90°+n°．
28．（8分）（2023春•徐州期末）已知：在△ABC中，∠BAC＝α．过AC边上的点D作DE⊥BC，垂足为点E．BF为△ABC的一条角平分线，DG为∠ADE的平分线．
（1）如图1，若α＝90°，点G在边BC上且不与点B重合．
①判断∠1与∠2的数量关系，并说明理由；
②判断BF与GD的位置关系，并说明理由；
（2）如图2，若0°＜α＜90°，点G在边BC上，DG与FB的延长线交于点H，用含α的代数式表示∠H，并说明理由；
（3）如图3，若0°＜α＜90°，点G在边AB上，DG与BF交于点M，用含α的代数式表示∠BMD，则∠BMD＝ 135°+α ．
（1）解：①∵∠ABC+∠C＝90°，∠CDE+∠C＝90°，
∴∠ABC＝∠CDE＝2∠1．
又∵∠CDE+∠ADE＝180°，
∴2∠1+2∠2＝180，即2（∠1+∠2）＝180°，
∴∠1+∠2＝90°．
②∵∠BFC＝∠BAC+∠ABF＝90°+∠1，∠GDC＝∠GDE+∠CDE＝∠2+2∠1＝∠1+∠2+∠1＝90°+∠1，
∴∠BFC＝∠GDC＝90°+∠1，
∴BF∥GD．
（2）∠H＝45°﹣α．
证明：∵∠H+∠BGH＝∠FBG，∠BGH＝∠DGE＝90°﹣∠EDG，
∴∠H+90°﹣∠EDG＝∠FBG，
∴∠H＝∠FBG+∠EDG﹣90°．
∵∠BGD＝∠EDG+90°，∠BFD＝∠ABF+α，∠BGD+∠BFD+∠FBG+∠FDG＝360°，
∴∠EDG+90°+∠ABF+α+∠FBG+∠FDG＝360°．
又∵∠ABF＝∠FBG，∠FDG＝∠EDG，
∴∠EDG+90°+∠ABF+α+∠FBG+∠FDG＝∠EDG+90°+∠FBG+α+∠FBG+∠EDG＝360°，
整理得2（∠EDG+∠FBG）＝360°﹣90°﹣α＝270﹣α，
∴∠FBG+∠EDG＝（270﹣α）＝135﹣α．将之代入∠H＝∠FBG+∠EDG﹣90°，
得∠H＝135﹣α﹣90°＝45°﹣α．
（3）∵∠BMD+90°+∠MBE+∠MDE＝360°，
∴∠BMD＝360°﹣90°﹣（∠MBE+∠MDE）＝270°﹣（∠MBE+∠MDE）．
又∵α+90°+∠ABE+∠ADE＝360°，∠ABE＝2∠MBE，∠ADE＝2∠MDE，
∴α+90°+2∠MBE+2∠MDE＝α+90°+2c（∠MBE+∠MBE）＝360°，
∴∠MBE+∠MBE＝（360°﹣90°﹣α）＝135°﹣α．将之代入∠BMD＝270°﹣（∠MBE+∠MDE），
得∠BMD＝270°﹣（135°﹣α）＝135°+α．
故答案为：135°+α