第1章《三角形的证明》【培优讲练】-2023-2024学年北师大版数学八年级下册章节复习讲义

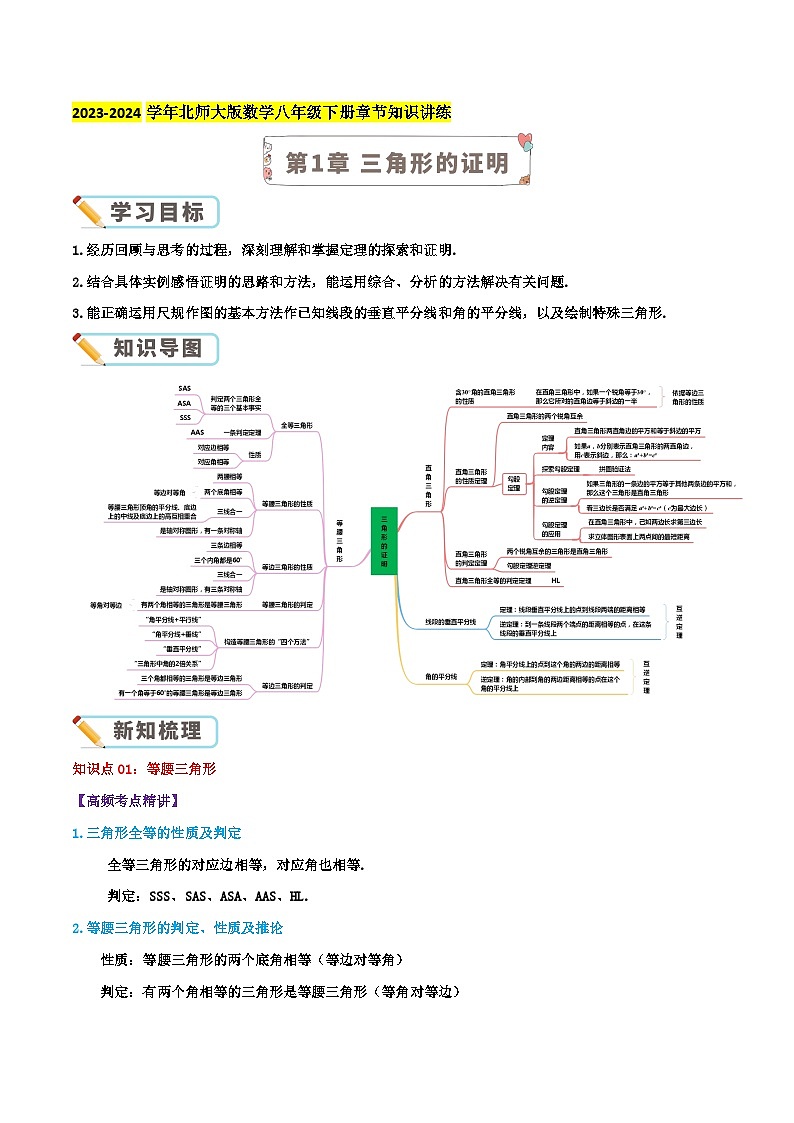
这是一份第1章《三角形的证明》【培优讲练】-2023-2024学年北师大版数学八年级下册章节复习讲义，文件包含第1章三角形的证明教师版docx、第1章三角形的证明学生版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。


1.经历回顾与思考的过程，深刻理解和掌握定理的探索和证明.
2.结合具体实例感悟证明的思路和方法，能运用综合、分析的方法解决有关问题.
3.能正确运用尺规作图的基本方法作已知线段的垂直平分线和角的平分线，以及绘制特殊三角形.
知识点01：等腰三角形
【高频考点精讲】
1.三角形全等的性质及判定
全等三角形的对应边相等，对应角也相等.
判定：SSS、SAS、ASA、AAS、HL.
2.等腰三角形的判定、性质及推论
性质：等腰三角形的两个底角相等（等边对等角）
判定：有两个角相等的三角形是等腰三角形（等角对等边）
推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）
3.等边三角形的性质及判定定理
性质定理：等边三角形的三个角都相等，并且每个角都等于60°；等边三角形的三条边都满足“三线合一”的性质；等边三角形是轴对称图形，有3条对称轴.
判定定理：有一个角是60°的等腰三角形是等边三角形；三个角都相等的三角形是等边三角形.
4.含30°的直角三角形的边的性质
定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
【易错点剖析】
等边三角形是中考中常考的知识点，并且有关它的计算也很常见，因此对于等边三角形的特殊数据要熟记于心，不如边长为a的等边三角形他的高是，面积是；含有30°的直角三角形揭示了三角形中边与角的关系，打破了以往那种只有角或边的关系，同时也为我们学习三角函数奠定了基础.
知识点02：直角三角形
【高频考点精讲】
1.勾股定理及其逆定理
定理：直角三角形的两条直角边的平方和等于斜边的平方.
逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.
2.命题与逆命题
命题包括题设和结论两部分；逆命题是将原命题的题设和结论交换位置得到的；正确的逆命题就是逆定理.
3.直角三角形全等的判定定理
定理：斜边和一条直角边对应相等的两个直角三角形全等（HL）
【易错点剖析】
①勾股定理的逆定理在语言叙述的时候一定要注意，不能说成“两条边的平方和等于斜边的平方”，应该说成“三角形两边的平方和等于第三边的平方”.
②直角三角形的全等判定方法，还有SSS,SAS,ASA,AAS,一共有5种判定方法.
知识点03：线段的垂直平分线
【高频考点精讲】
1.线段垂直平分线的性质及判定
性质：线段垂直平分线上的点到这条线段两个端点的距离相等.
判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
2.三角形三边的垂直平分线的性质
三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.
3.如何用尺规作图法作线段的垂直平分线
分别以线段的两个端点A、B为圆心，以大于AB的长为半径作弧，两弧交于点M、N；作直线MN，则直线MN就是线段AB的垂直平分线.
【易错点剖析】
①注意区分线段的垂直平分线性质定理和判定定理,注意二者的应用范围；
②利用线段的垂直平分线定理可解决两条线段的和距离最短问题.
知识点04：角平分线
【高频考点精讲】
1.角平分线的性质及判定定理
性质：角平分线上的点到这个角的两边的距离相等；
判定：在一个角的内部，且到角的两边的距离相等的点，在这个角的平分线上.
2.三角形三条角平分线的性质定理
性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.
3.如何用尺规作图法作出角平分线
【易错点剖析】
①注意区分角平分线性质定理和判定定理,注意二者的应用范围；
②几何语言的表述，这也是证明线段相等的一种重要的方法.遇到角平分线时，要构造全等三角形.
检测时间：120分钟 试题满分：100分 难度系数：0.51
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）（2023秋•包河区期末）如图，△ABC中，∠C＝90°，∠B＝30°，D在边BC上，DE垂直平分AB，DE＝3，则BC＝（ ）
A．7B．8C．9D．10
解：∵∠C＝90°，∠B＝30°，
∴∠BAC＝90°﹣30°＝60°，
∵DE垂直平分AB，
∴DA＝DB，
∴∠DAB＝∠B＝30°，
∴∠CAD＝∠BAC﹣∠BAD＝30°，
∴∠BAD＝∠CAD，
∵DC⊥AC，DM⊥AB，
∴DC＝DE＝3，
∵∠B＝30°，∠BED＝90°，
∴BD＝2DE＝2×3＝6，
∴BC＝BD+CD＝6+3＝9．
故选：C．
2．（2分）（2023秋•海口期末）如图，O是△ABC内一点，OA＝OB＝OC，∠BAC＝70°，则∠1等于（ ）
A．20°B．30°C．35°D．40°
解：∵OA＝OB＝OC，
∴∠OAB＝∠OBA，∠1＝∠OCB，∠OAC＝∠OCA，
∵∠BAC＝70°，
∴∠OAB+∠OAC＝70°，
∴∠OBA+∠OCA＝70°，
∴∠1+∠OCB＝180°﹣∠BAC﹣（∠OBA+∠OCA）＝40°，
∴∠1＝∠OCB＝20°，
故选：A．
3．（2分）（2023秋•宁波期末）如图，AD是△ABC的角平分线，E是AB的中点，△ABC的面积为21，AC＝6，AB＝8，则△BED的面积为（ ）
A．B．5C．6D．
解：∵AD是△ABC的角平分线，
∴点D到AB和AC的距离相等，
∴S△ABD：S△ACD＝AB：AC＝8：6＝4：3，
∴S△ABD＝S△ABC＝×21＝12，
∵E是AB的中点，
∴S△BED＝S△ABD＝×12＝6．
故选：C．
4．（2分）（2023秋•柘城县期末）如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴负半轴于点M，交y轴负半轴于点N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧在第三象限交于点P．若点P的坐标为（a，b），则a与b的数量关系为（ ）
A．a+b＝0B．a+b＞0C．a﹣b＝0D．a﹣b＞0
解：根据作图方法可得点P在第三象限角平分线上；点P到x轴、y轴的距离相等；
∴a﹣b＝0．
故选：C．
5．（2分）（2023秋•金寨县期末）如图，在△ABC中，∠ABC＝3∠C，∠1＝∠2，BE⊥AE，AB＝5，BE＝3，则AC＝（ ）
A．10B．11C．13D．15
解：延长BE交AC于M，
∵BE⊥AE，
∴∠AEB＝∠AEM＝90°
∴∠3＝90°﹣∠1，∠4＝90°﹣∠2，
∵∠1＝∠2，
∴∠3＝∠4，
∴AB＝AM＝5，
∵BE⊥AE，
∴BM＝2BE＝6，
∵∠4是△BCM的外角，
∴∠4＝∠5+∠C，
∵∠ABC＝3∠C，
∴∠ABC＝∠3+∠5＝∠4+∠5，
∴3∠C＝∠4+∠5＝2∠5+∠C，
∴∠5＝∠C，
∴CM＝BM＝6，
∴AC＝AM+CM＝AB+2BE＝11．
故选：B．
6．（2分）（2023秋•化州市期末）已知，如图长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ）
A．3cm2B．4cm2C．6cm2D．12cm2
解：将此长方形折叠，使点B与点D重合，∴BE＝ED．
∵AD＝9cm＝AE+DE＝AE+BE．
∴BE＝9﹣AE，
根据勾股定理可知AB2+AE2＝BE2．
解得AE＝4．
∴△ABE的面积为3×4÷2＝6．故选：C．
7．（2分）（2023秋•五华区期末）如图，在△ABC中，AB＝AC，AD是∠BAC的平分线，若BD＝5，则CD等于（ ）
A．3B．4C．5D．6
解：∵AD是∠BAC的平分线，AB＝AC，
∴AD为BC边上的中线，
∴CD＝BD＝5．
故选：C．
8．（2分）（2023秋•彰武县期末）如图，以Rt△ABC的三条边作三个正三角形，则S1、S2、S3、S4的关系为（ ）
A．S1+S2+S3＝S4B．S1+S2＝S3+S4
C．S1+S3＝S2+S4D．不能确定
解：如图，设Rt△ABC的三条边AB＝c，AC＝b，BC＝a，
∵△ACG，△BCH，△ABF是等边三角形，
∴S1＝S△ACG﹣S5＝b2﹣S5，S3＝S△BCH﹣S6＝a2﹣S6，
∴S1+S3＝（a2+b2）﹣S5﹣S6，
∵S2+S4＝S△ABF﹣S5﹣S6＝c2﹣S5﹣S6，
∵c2＝a2+b2，
∴S1+S3＝S2+S4，
故选：C．
9．（2分）（2023秋•宁江区期末）如图，AD是等边△ABC的一条中线，若在边AC上取一点E，使得AE＝AD，则∠EDC的度数为（ ）
A．30°B．20°C．25°D．15°
解：∵△ABC为等边三角形，
∴∠BAC＝60°，
∵AD是等边△ABC的一条中线，
∴AD⊥BC，∠CAD＝∠BAC＝30°，
∵AE＝AD，
∴∠ADE＝∠AED，
∵∠ADE+∠AED+∠CAD＝180°，
∴∠ADE＝75°，
∴∠EDC＝90°﹣75°＝15°，
故选：D．
10．（2分）（2022秋•河间市校级期末）如图，在△ABC中，AB＝AC＝5，BC＝6，则AC边上的高BD的长为（ ）
A．4B．C．D．5
解：过A作AE⊥BC于点E，
∵AB＝AC，
∴△ABC是等腰三角形，
∵AE⊥BC，
∴EB＝EC＝CB＝3，
在Rt△ABE中，AE＝＝4，
∴S△ABC＝•AC•BD＝•BC•AE＝×6×4＝12，
∴5×BD＝12，
解得BD＝．
故选：C．
二．填空题（共10小题，满分20分，每小题2分）
11．（2分）（2023秋•海口期末）如图，△ABC是边长为5的等边三角形，点D，E分别在BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，若BD＝2，则DF的长为 6 ．
解：∵△ABC是边长是5的等边三角形，
∴∠B＝∠ACB＝60°，BC＝5，
∵DE∥AB，
∴∠EDC＝∠B＝60°，
∴∠DEC＝180°﹣60°﹣60°＝60°，
∴△EDC是等边三角形，
∴DE＝CD，
∵BD＝2，
∴CD＝BC﹣BD＝5﹣2＝3，
∴DE＝CD＝3，
∵DE⊥EF，
∴∠DEF＝90°，
∴∠F∠＝90°﹣∠EDC＝30°，
∴DF＝2DE＝6．
故答案为：6．
12．（2分）（2023秋•成华区期末）如图，我国汉代数学家赵爽证明勾股定理时创制了一幅由4个全等的直角三角形和一个小正方形组成的“勾股圆方图”，后人称之为“赵爽弦图”．设直角三角形的直角边长为a，b，斜边长为c，若b﹣a＝4，c＝20，则每个直角三角形面积为 96 ．
解：∵直角三角形的直角边长为a，b，斜边长为c，b﹣a＝4，c＝20，
∴a2+b2＝c2＝400，（b﹣a）2＝16，
∴a2+b2﹣2ab＝16，
∴400﹣2ab＝16，
∴2ab＝384，
∴＝96，
即每个直角三角形面积为96，
故答案为：96．
13．（2分）（2023秋•思明区校级期末）如图，在等边△ABC中，BC＝2，D是AB的中点，过点D作DF⊥AC于点F，过点F作EF⊥BC于点E，则BE的长为 ．
解：∵△ABC为等边三角形，
∴∠A＝∠C＝60°，AB＝AC＝BC＝2，
∵DF⊥AC，FE⊥BC，
∴∠AFD＝∠CEF＝90°，
∴∠ADF＝∠CFE＝30°，
∴AF＝AD，CE＝CF，
∵点D是AB的中点，
∴AD＝1，
∴AF＝，CF＝，CE＝，
∴BE＝BC﹣CE＝2﹣，
故答案为：．
14．（2分）（2023秋•铁西区期末）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC与点E，∠A＝∠ABE．若AC＝7，BC＝4，则BD的长为 ．
解：∵CD平分∠ACB，
∴∠BCD＝∠ECD，
∵BE⊥CD，
∴∠BDC＝∠EDC＝90°，
∵CD＝CD，
∴△BDC≌△EDC（ASA），
∴BC＝CE＝4，BD＝DE，
又∵∠A＝∠ABE，
∴AE＝BE，
∵AC＝7，BC＝4，
∴AE＝AC﹣CE＝3，
∴BE＝AE＝3，
∴BD＝BE＝，
故答案为：．
15．（2分）（2023秋•明水县期末）如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，△ABC的面积是 31.5 ．
解：作OE⊥AC，OF⊥AB，垂足分别为E、F，连接OA，
∵OB，OC分别平分∠ABC和∠ACB，OD⊥BC，
∴OD＝OE＝OF，
∴S△ABC＝S△OBC+S△OAC+S△OAB
＝×OD×BC+×OE×AC+×OF×AB
＝×OD×（BC+AC+AB）
＝×3×21＝31.5．
故答案为：31.5．
16．（2分）（2023秋•藁城区期末）如图，∠MAN是一个钢架，∠MAN＝5°，为使钢架更牢固，需在其内部焊接一些钢管，如CD、DE、EF⋯⋯若焊接的钢管的长度都与AC的长度相等，则最多能焊接 17 根．
解：∵添加的钢管长度都与CD相等，∠MAN＝5°，
∴∠DCE＝∠DEC＝10°，
…，
从图中我们会发现有好几个等腰三角形，即第一个等腰三角形的底角是5°，第二个是10°，第三个是15°，第四个是20°，第五个是25°，第六个是30°，第七个是35°，第八个是40°，…，第十八个是90°就不存在了．
所以一共有17个．
故答案为：17．
17．（2分）（2023秋•惠安县期末）如图是2×4正方形网格图，点A、B、C、D、E都是格点，则∠BAC﹣∠BDE＝ 45 °．
解：，
作△AFG≌△DBE，连接BF，
∴∠FAG＝∠BDE，
∠BAC﹣∠BDE＝∠BAC﹣∠FAC＝∠BAF，
∵AC＝BE，∠BEF＝∠ACB，BC＝EF，
∴△ABC≌△BFE，
∴∠BAC＝∠FBE，AB＝BF，
∵∠BAC+∠ABC＝90°，
∴∠ABC+∠FBE＝90°，
即∠ABF＝90°，
∵AB＝BF，
∴△ABF是等腰直角三角形，
∴∠BAF＝45°，
故答案为：45．
18．（2分）（2023秋•惠州期末）如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD＝3，AB＝10，则△ABD的面积是 15 ．
解：如图，作DE⊥AB于E，
由基本尺规作图可知，AD是△ABC的角平分线，
∵∠C＝90°，DE⊥AB，
∴DE＝DC＝3，
∴△ABD的面积＝×AB×DE＝×10×3＝15，
故答案为：15．
19．（2分）（2023秋•龙岗区校级期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝16，AB＝20，动点D从点A出发，沿线段AB以每秒2个单位的速度向B运动，过点D作DF⊥AB交BC所在的直线于点F，连接AF，CD．设点D运动时间为t秒．当△ABF是等腰三角形时，则t＝ 5或或4 秒．
解：在Rt△ABC中，∠ACB＝90°，AC＝16，AB＝20，
由勾股定理得：，
当FA＝FB时，DF⊥AB，
∴，
∴t＝10÷2＝5；
当AF＝AB＝20时，∠ACB＝90°，
则BF＝2BC＝24，
∴，即，
解得：，
由勾股定理得：，
∴；
当BF＝AB＝20时，
∵BF＝20，BC＝12，
∴CF＝BF﹣BC＝8，
由勾股定理得：，
∵BF＝BA，FD⊥AB，AC⊥BF，
∴DF＝AC＝16，
∴，
∴t＝8÷2＝4；
综上所述，△ABF是等腰三角形时，t的值为5或或4，
故答案为：5或或4．
20．（2分）（2023秋•东城区期末）如图，Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝6，D是线段AB上一个动点，以BD为边在△ABC外作等边△BDE．若F是DE的中点，当CF取最小值时，△BDE的周长为 18 ．
解：连接BF，过点C作CH⊥BF．交BF的延长线于H，
∵△BDE是等边三角形，点F是DE的中点，
∴∠ABF＝30°，
∴点F在射线BF上运动，
当点F与点H重合时，CF最小，
∵∠ACB＝90°，∠ABC＝30°，
∴∠A＝60°，AB＝2AC＝12，
∵∠ABF＝30°，
∴∠BD'H＝∠AD'C＝60°，
∴△ACD'是等边三角形，
∴AD'＝AC＝6，
∴BD'＝AB﹣AD'＝12﹣6＝6，
∴△BDE的周长为：18，
故答案为：18．
三．解答题（共8小题，满分60分）
21．（6分）（2023秋•李沧区期末）已知：如图，D是△ABC的边BC上一点，DE⊥AC，垂足为E，F是DE延长线上一点，AF∥BC，∠B＝∠F．
（1）求证：AB∥DF；
（2）若AB＝6，AC＝8，求BC的长．
（1）证明：∵AF∥BC，
∴∠F＝∠FDC，
∵∠B＝∠F，
∴∠B＝∠FDC，
∴AB∥FD；
（2）解：∵DE⊥AC，
∴∠DEC＝90°，
∵AB∥DF，
∴∠BAC＝∠DEC＝90°，
∵AB＝6，AC＝8，
∴BC＝＝＝10，
∴BC的长为10．
22．（6分）（2023秋•和田地区期末）已知：如图△ABC中AC＝6cm，AB＝8cm，BD平分∠ABC，CD平分∠ACB，过D作直线平行于BC，交AB，AC于E，F．
（1）求证：△DFC是等腰三角形；
（2）求△AEF的周长．
（1）证明：∵EF∥BC，
∴∠FDC＝∠DCB，
∵CD平分∠ACB，
∴∠FCD＝∠DCB，
∴∠FDC＝∠FCD，
∴FD＝FC，
∴△DFC是等腰三角形；
（2）∵EF∥BC，
∴∠EDB＝∠DBC，
∵BD平分∠ABC，
∴∠EBD＝∠DBC，
∴∠EDB＝∠EBD，
∴ED＝EB，
∵AC＝6cm，AB＝8cm，
∴△AEF的周长为：AE+EF+AF
＝AE+ED+FD+AF
＝AE+EB+FC+AF
＝AB+AC
＝8+6
＝14（cm）．
23．（8分）（2023秋•城关区期末） 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列三个问题：
（1）如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理c2＝a2+b2．
（2）如图2，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AC＝4，BC＝3，求CD的长度；
（3）如图1，若大正方形的面积是13，小正方形的面积是1，求（a+b）2的值（a＜b）．
解：（1）如图1，大正方形的面积＝c2＝4×，
整理得，c2＝a2+b2；
（2）在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，
∴AB＝＝5，
∵，
∴CD＝；
（3）∵大正方形的面积是13，小正方形的面积是1，
∴c2＝13，（b﹣a）2＝1，
∴a2+b2﹣2ab＝1，
∴2ab＝12，
∴（a+b）2＝a2+b2+2ab＝13+12＝25，
即（a+b）2的值为25．
24．（8分）（2023秋•船营区校级期末）如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝3，点P从点A出发，沿射线AC以每秒2个单位长度的速度运动．设点P的运动时间为t秒（t＞0）．
（1）当点P在AC的延长线上运动时，CP的长为 2t﹣4 ；（用含t的代数式表示）
（2）若点P在∠ABC的角平分线上，求t的值；
（3）在整个运动中，直接写出△ABP是等腰三角形时t的值．
解：（1）∵在△ABC中，∠ACB＝90°，AB＝5，BC＝3，
∴由勾股定理得：，
∵已知点P从点A出发，以每秒2个单位长度的速度运动，
∴当点P在AC的延长线上时，点P运动的长度为：AC+CP＝2t，
∵AC＝4，
∴CP＝2t﹣AC＝2t﹣4．
故答案为：2t﹣4．
（2）过点P作PM⊥AB于点M，如图所示：
∵∠ACB＝90°，
∴PC⊥BC，
∵点P在∠ABC的角平分线上，PM⊥AB，
∴PC＝PM，
又∵PB＝PB，
∴Rt△PCB≌Rt△PMB（HL），
∴CB＝MB，
∴AM＝AB﹣MB＝AB＝BC＝5﹣3＝2，
设PM＝PC＝x，则AP＝4﹣x，
在Rt△APM中，AM2+PM2＝AP2，
∴22+x2＝（4﹣x）2，
解得：，
，
即若点P在∠ABC的角平分线上，则t的值为．
（3）当AB作为底边时，如图所示：
则PA＝PB，设PA＝a，则PC＝AC﹣AP＝4﹣a，
在Rt△PCB中，PB2＝PC2+CB2，
a2＝（4﹣a）2+32，
解得：，
此时；
当AB作为腰时，如图所示：
AP1＝AB＝5，此时；
AB＝BP2时，
∵BC⊥AP2，
∴AP2＝2AC＝8，
此时t＝8÷2＝4，
综上分析可知，t的值为或或4．
25．（8分）（2023秋•双辽市期末）如图，已知点D，E分别是△ABC的边BA和BC延长线上的点，作∠DAC的平分线AF，若AF∥BC．
（1）求证：△ABC是等腰三角形；
（2）作∠ACE的平分线交AF于点G，若∠B＝40°，求∠AGC的度数．
（1）证明：∵AF平分∠DAC，
∴∠DAF＝∠CAF，
∵AF∥BC，
∴∠DAF＝∠B，∠CAF＝∠ACB，
∴∠B＝∠ACB，
∴△ABC是等腰三角形；
（2）解：∵AB＝AC，∠B＝40°，
∴∠ACB＝∠B＝40°，
∴∠BAC＝100°，
∴∠ACE＝∠BAC+∠B＝140°，
∵CG平分∠ACE，
∴ACE＝70°，
∵AF∥BC，
∴∠AGC＝180°﹣∠BCG＝180°﹣40°﹣70°＝70°．
26．（8分）（2022秋•唐山期末）在△ABC中，AB≠AC，∠ABC与∠ACB的平分线交于O点，MN经过点O，与AB，AC相交于点M，N，且MN∥BC．
（1）如图1，直接写出图中所有的等腰三角形；猜想：MN与BM，CN之间有怎样的数量关系，并说明理由．
（2）如图2，△ABC中，∠ABC的平分线BO与三角形外角平分线CO交于点O，过O点作OM∥BC交AB于点M，交AC于点N．图中有等腰三角形吗？如果有，分别指出它们．写出MN与BM，CN之间的数量关系，并说明理由．
解：（1）BQ平分∠ABC，CO平分∠ACB，
∴∠MBO＝∠OBC，∠NCO＝∠OCB，
∵MN∥BC，
∴∠MOB＝∠OBC，∠NOC＝∠OCB，
∴∠MBO＝∠MOB，∠NOC＝∠NCO，
∴BM＝OM，CN＝ON，
∴△BMO，△CNO，是等腰三角形
即图中等腰三角形有△BMO，△CNO，；
MN与BM、CN之间的关系是MN＝BN+CN；
（2）BQ平分∠ABC，CO平分∠ACB，，
∴∠MBO＝∠OBC，∠NCO＝∠OCH，
∵OM∥BC，
∴∠MOB＝∠OBC，∠NOC＝∠OCH，
∴∠MBO＝∠MOB，∠NOC＝∠NCO，
∴BM＝OM，CN＝ON，
∴△BMO，△CNO是等腰三角形
即图中等腰三角形有△BMO，△CNO；
MN与BM、CN之间的关系是MN＝BN﹣CN．．
27．（8分）（2023秋•宜州区期末）如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，∠OCD＝60°，连接OD．
（1）求证：△OCD是等边三角形；
（2）当α＝150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形．
证明：（1）∵△BOC≌△ADC，
∴OC＝DC，
∵∠OCD＝60°，
∴△OCD是等边三角形．
解：
（2）△AOD是直角三角形．
理由如下：
∵△OCD是等边三角形，
∴∠ODC＝60°，
∵△BOC≌△ADC，α＝150°，
∴∠ADC＝∠BOC＝α＝150°，
∴∠ADO＝∠ADC﹣∠ODC＝150°﹣60°＝90°，
∴△AOD是直角三角形．
（3）∵△OCD是等边三角形，
∴∠COD＝∠ODC＝60°．
∵∠AOB＝110°，∠ADC＝∠BOC＝α，
∴∠AOD＝360°﹣∠AOB﹣∠BOC﹣∠COD＝360°﹣110°﹣α﹣60°＝190°﹣α，
∠ADO＝∠ADC﹣∠ODC＝α﹣60°，
∴∠OAD＝180°﹣∠AOD﹣∠ADO＝180°﹣（190°﹣α）﹣（α﹣60°）＝50°．
①当∠AOD＝∠ADO时，190°﹣α＝α﹣60°，
∴α＝125°．
②当∠AOD＝∠OAD时，190°﹣α＝50°，
∴α＝140°．
③当∠ADO＝∠OAD时，
α﹣60°＝50°，
∴α＝110°．
综上所述：当α＝110°或125°或140°时，△AOD是等腰三角形．
28．（8分）（2023秋•新抚区期末）在等边△ABC中，点E是AB上的动点，点E与点A、B不重合，点D在CB的延长线上，且EC＝ED．
（1）如图1，若点E是AB的中点，求证：BD＝AE；
（2）如图2，若点E不是AB的中点时，（1）中的结论“BD＝AE”能否成立？若不成立，请直接写出BD与AE数量关系，若成立，请给予证明．
（1）证明：∵△ABC是等边三角形，
∴∠ABC＝∠ACB＝60°，
∵点E是AB的中点，
∴CE平分∠ACB，AE＝BE，
∴∠BCE＝30°，
∵ED＝EC，
∴∠D＝∠BCE＝30°．
∵∠ABC＝∠D+∠BED，
∴∠BED＝30°，
∴∠D＝∠BED，
∴BD＝BE．
∴AE＝DB．
（2）解：AE＝DB；
理由：过点E作EF∥BC交AC于点F．如图2所示：
∴∠AEF＝∠ABC，∠AFE＝∠ACB．
∵△ABC是等边三角形，
∴∠ABC＝∠ACB＝∠A＝60°，AB＝AC＝BC，
∴∠AEF＝∠ABC＝60°，∠AFE＝∠ACB＝60°，
即∠AEF＝∠AFE＝∠A＝60°，
∴△AEF是等边三角形．
∴∠DBE＝∠EFC＝120°，∠D+∠BED＝∠FCE+∠ECD＝60°，
∵DE＝EC，
∴∠D＝∠ECD，
∴∠BED＝∠ECF．
在△DEB和△ECF中，
，
∴△DEB≌△ECF（AAS），
∴DB＝EF，
∴AE＝BD