高考数学复习第六章　第一节　平面向量的概念及其线性运算（导学案）

这是一份高考数学复习第六章　第一节　平面向量的概念及其线性运算（导学案），共16页。学案主要包含了课程标准，必备知识 精归纳，常用结论，基础小题 固根基，方法提炼，对点训练，加练备选，一题多变等内容，欢迎下载使用。
第六章 平面向量、复数
第一节 平面向量的概念及其线性运算
【课程标准】
1.通过对力、速度、位移等的分析,了解平面向量的实际背景,理解平面向量的意义和两个向量相等的含义.
2.理解平面向量的几何表示和基本要素.
3.借助实例和平面向量的几何表示,掌握平面向量加、减运算及运算规则,理解其几何意义.
4.通过实例分析,掌握平面向量数乘运算及运算规则,理解其几何意义.理解两个平面向量共线的含义.
5.了解平面向量的线性运算性质及其几何意义.
【必备知识 精归纳】
1.平面向量的有关概念
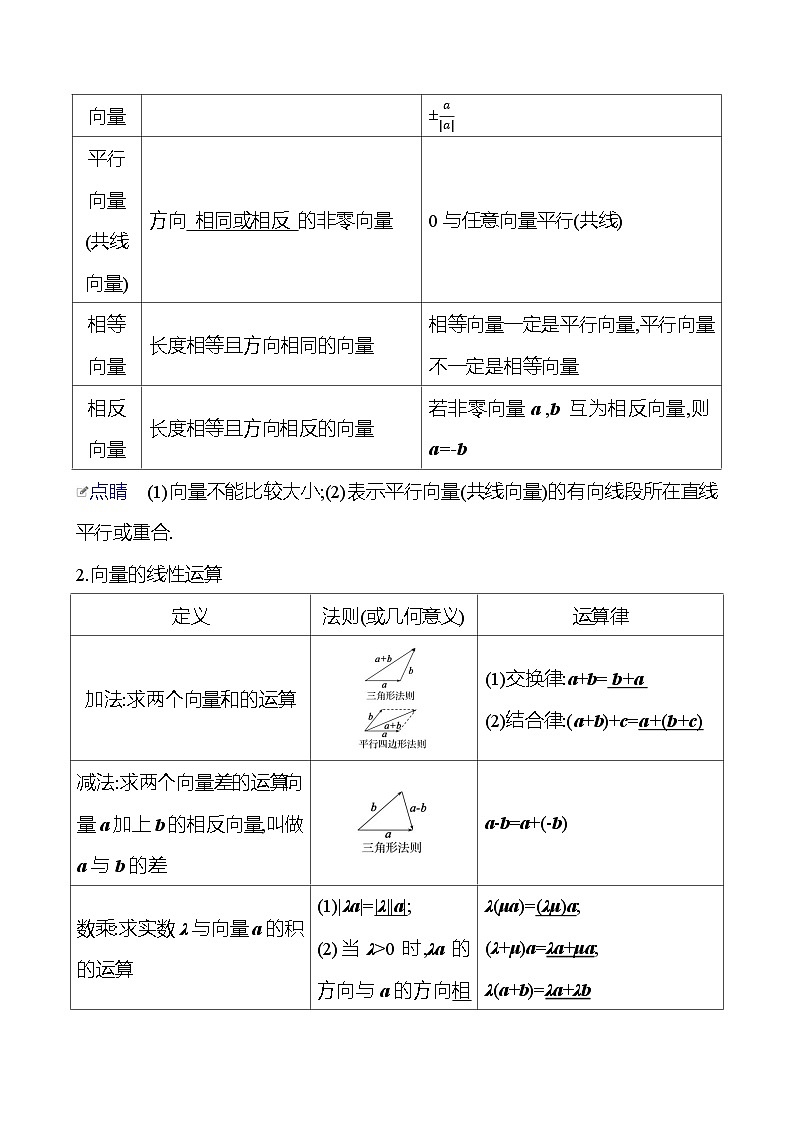
点睛 (1)向量不能比较大小;(2)表示平行向量(共线向量)的有向线段所在直线平行或重合.
2.向量的线性运算
点睛 三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
3.共线向量定理
向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
【常用结论】
1.若F为线段AB的中点,O为平面内任意一点,则=12(+);
2.对于任意两个向量a,b,都有||a|-|b||≤|a±b|≤|a|+|b|.
【基础小题 固根基】
1.(向量有关概念理解错误)下列关于向量的结论,其中正确的为( B )
A.若|a|=|b|,则a=b或a=-b
B.非零向量a与b平行,则a与b的方向相同或相反
C.向量与向量是共线向量,则A,B,C,D四点在一条直线上
D.若向量a与b同向,且|a|=|b|,则a>b
解析：若|a|=|b|,但a,b方向不能确定,选项A错误;非零向量a与b平行,则a与b的方向相同或相反,选项B正确;共线向量所在的直线可以重合,也可以平行,则A,B,C,D四点不一定在一条直线上,选项C错误;向量不能比较大小,选项D错误.
2.(结论1)设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内的任意一点,则+++等于( D )
A. B.2 C.3 D.4
解析：如图,
在△OAC中,M为AC的中点,所以+=2,
在△OBD中,M为BD的中点,所以+=2,所以+++=4.
3.(正确应用向量加法的两个法则)如图,已知正方形ABCD的边长为1,=a,=b,=c,则|a+b+c|= .
解析：由已知得a+b=+==c,如图,延长AC至E,使||=||,
则a+b+c==2,所以|a+b+c|=22.
答案:22
4.(教材变式)点C在线段AB上,且ACCB=73,则= ,= .
解析：由已知条件画图如下,
由图形可知,=710,=-310.
答案:710 -310
5.(结论2)设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为 , .
解析：当a,b共线同向时,|a+b|=|a|+|b|=8+12=20,
当a,b共线反向时,|a+b|=||a|-|b||=4.当a,b不共线时,||a|-|b||0时,λa的方向与a的方向相同;
当λ