高考数学复习第九章　第六节　第一课时　双曲线的定义、标准方程及其几何性质（导学案）

这是一份高考数学复习第九章　第六节　第一课时　双曲线的定义、标准方程及其几何性质（导学案），共20页。

1.了解双曲线的定义、几何图形和标准方程以及简单几何性质.
2.通过双曲线与方程的学习,进一步体会数形结合的思想.
第1课时 双曲线的定义、标准方程及其几何性质
1.双曲线的定义
满足下列两个条件
(1)在同一个平面内动点P和两定点F1,F2;
(2)||PF1|-|PF2||为定值,且0<||PF1|-|PF2||<|F1F2|的动点P的轨迹为双曲线.
点睛(1)定义中的绝对值如果去掉,其轨迹为双曲线的一支.
(2)当||PF1|-|PF2||=|F1F2|时,动点P的轨迹为两条射线.
(3)当||PF1|-|PF2||>|F1F2|时,动点P不存在,无轨迹.
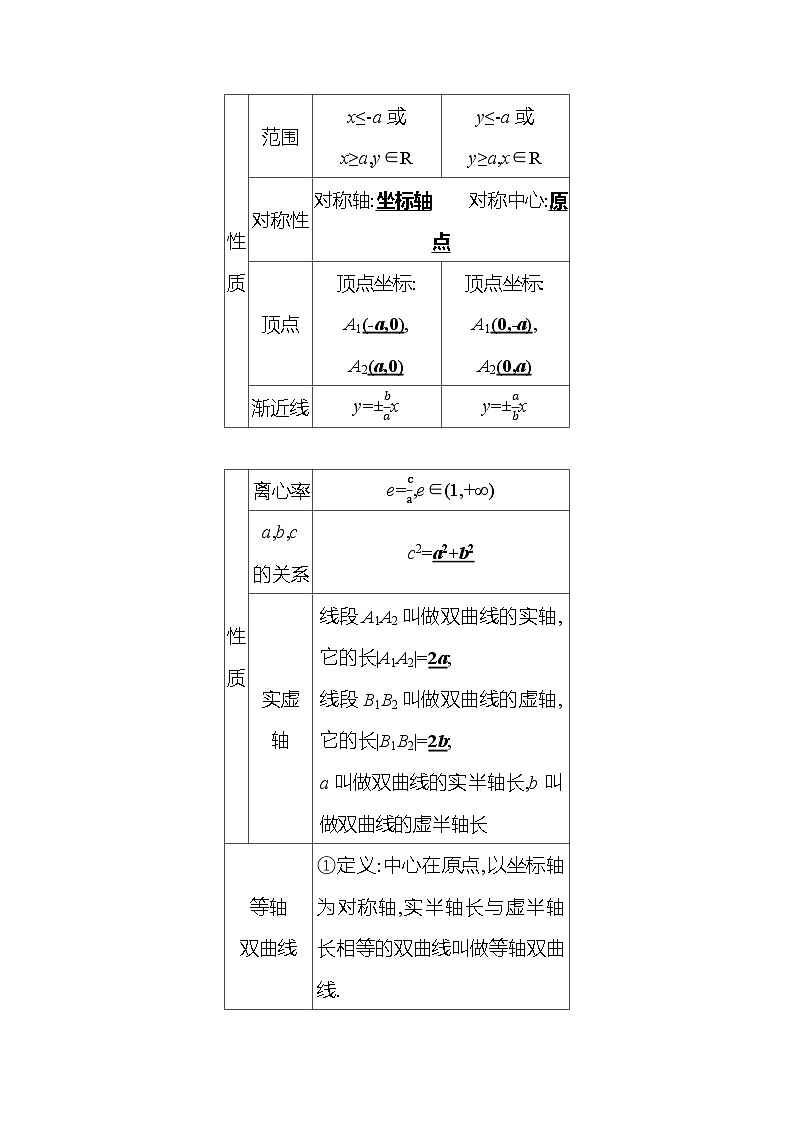
2.双曲线的标准方程和几何性质
点睛
1.双曲线的标准方程中对a,b的要求只是a>0,b>0.
2.注意区分双曲线中的a,b,c大小关系与椭圆中的a,b,c大小关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2.
1.焦点到渐近线的距离为b.
2.若P是双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,则|PF1|min=a+c,|PF2|min=c-a.
3.设P,A,B是双曲线上的三个不同的点,其中A,B关于原点对称,直线PA,PB斜率存在且不为0,则直线PA与PB的斜率之积为b2a2.
4.双曲线的离心率公式可表示为e=1+b2a2.
1.(教材变式)已知双曲线x2-y216=1上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于 .
解析：设双曲线的焦点分别为F1,F2,|PF1|=4,
则||PF1|-|PF2||=2,故|PF2|=6或2,又双曲线上的点到同侧焦点的距离的最小值为c-a=17-1,故|PF2|=6.
答案:6
2.(混淆焦点位置)已知双曲线的两个焦点分别为F1(0,-5),F2(0,5),双曲线上一点P与F1,F2的距离差的绝对值等于6,则双曲线的标准方程为( )
A.x29-y216=1B.x216-y29=1
C.y29-x216=1D.y216-x29=1
解析：选C.由题意,c=5,2a=6,所以a=3,
则b=c2-a2=4,结合条件可知,
双曲线的标准方程为y29-x216=1.
3.(结论4)双曲线y23-x2=1的离心率为( )
A.32B.62C.233D.263
解析：选C.双曲线y23-x2=1的焦点在y轴上,
a=3,b=1,
所以离心率为ca=1+b2a2=1+13=233.
4.(结论1)若双曲线x2a2-y2b2=1的焦点F(3,0)到其渐近线的距离为5,则双曲线的方程为( )
A.x24-y25=1B.x25-y24=1
C.x23-y26=1D.x26-y23=1
解析：选A.因为焦点为F(3,0),所以c=3,
根据双曲线的焦点到渐近线的距离为b,
得b=5,所以双曲线方程为x24-y25=1.
5.(教材提升)若双曲线x2a2-y2=1(a>0)的一条渐近线方程为y=12x,则a= .
解析：焦点在x轴上的双曲线的渐近线方程为
y=bax,而b=1,ba=12,所以a=2.
答案:2
双曲线定义及应用
[典例1](1)已知F1,F2分别为双曲线x2-y2=2的左、右焦点,点P在双曲线的右支上,且PF22=8F1F2,则PF1=( )
A.62B.22
C.22+4D.22+2
解析：选A.在双曲线x2-y2=2中,
a=2,b=2,c=2,
因为PF22=8F1F2=8×4=32,
所以PF2=42,
又PF1-PF2=2a=22,
所以PF1=22+PF2=62.
(2)(2023·厦门模拟)已知F1,F2分别是双曲线C:x24-y2=1的左、右焦点,动点P在双曲线的左支上,点Q为圆G:x2+(y+2)2=1上一动点,则|PQ|+|PF2|的最小值为( )
A.6B.7C.3+5D.5
解析：选A.如图,圆G的圆心为(0,-2),半径为1,F1(-5,0),|PQ|+|PF2|=|PQ|+|PF1|+2a≥|PG|-1+|PF1|+4,
当P,G,F1三点共线时,|PQ|+|PF2|最小,最小值为|GF1|+3,
而|GF1|=(5)2+22=3,所以|GF1|+3=6.
1.双曲线定义的主要应用
(1)判定平面内动点与两定点的轨迹是否为双曲线,进而根据要求可求出曲线方程.
(2)在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF1|-|PF2||=2a,运用平方的方法,建立与|PF1|·|PF2|的联系.
2.与双曲线两焦点有关的问题常利用定义求解.
3.如果题设条件涉及动点到两定点的距离,求轨迹方程时可考虑能否应用定义求解.
1. 已知平面内两定点F1(-3,0),F2(3,0),下列条件中满足动点P的轨迹为双曲线的是( )
A.PF1-PF2=±7
B.PF1-PF2=±6
C.PF1-PF2=±4
D.PF12-PF22=±6
解析：选C.由题意,因为F1F2=6,
所以由双曲线的定义知,
当0动点P的轨迹为双曲线.
2.已知F是双曲线x24-y212=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为( )
A.9B.8C.7D.6
解析：选A.由x24-y212=1,得a2=4,b2=12,
则a=2,b=23,c=a2+b2=4,
所以左焦点为F(-4,0),右焦点为F'(4,0),
则由双曲线的定义得PF-PF'=2a=4,
因为点A(1,4)在双曲线的两支之间,
所以PA+PF'≥AF'=32+42=5,
所以PF+PA≥9,
当且仅当A,P,F'三点共线时取等号,
所以|PF|+|PA|的最小值为9.
【加练备选】
设P(x,y)是双曲线x25-y24=1的右支上的点,则代数式x2+y2-2y+1-
x2+y2-6x+9的最小值为( )
A.10B.25-10
C.10-5D.5+6-3
解析：选B.x2+y2-2y+1-x2+y2-6x+9=x2+(y-1)2-(x-3)2+y2,
设A(0,1),F(3,0),上式表示PA-PF,由于双曲线x25-y24=1的左焦点为F'(-3,0),右焦点为F(3,0),
双曲线的实轴2a=25,PF=PF'-2a=PF'-25,
PA-PF=PA-PF'+25=
-(PF'-PA)+25,
PF'-PA≤AF'=32+12=10,
当P在F'A的延长线与双曲线右支的交点处时取到等号,
所以PA-PF=-(PF'-PA)+25的最小值为25-10.
双曲线的标准方程
角度1 定义法求双曲线的标准方程
[典例2](1)在平面直角坐标系中,已知△ABC的顶点A(-3,0),B(3,0),其内切圆圆心在直线x=2上,则顶点C的轨迹方程为( )
A.x24-y25=1(x>2)
B.x29-y25=1(x>3)
C.x29+y25=1(0D.x29+y24=1(0解析：选A.如图,设△ABC与圆的切点分别为D,E,F,则有|AD|=|AE|=5,|BF|=|BE|=1,
|CD|=|CF|,所以|CA|-|CB|=5-1=4.
根据双曲线定义,所求轨迹是以A,B为焦点,实轴长为4的双曲线的右支(右顶点除外),
即c=3,a=2,又c2=a2+b2,所以b2=5,
所以方程为x24-y25=1(x>2).
(2)已知两圆C1:(x+4)2+y2=2,C2:(x-4)2+y2=2,动圆M与两圆C1,C2都相切,则动圆圆心M的轨迹方程是( )
A.x=0B.x22-y214=1(x≥2)
C.x22-y214=1D.x22-y214=1或x=0
解析：选D.动圆M与两圆C1,C2都相切,有四种情况:①动圆M与两圆都外切;②动圆M与两圆都内切;③动圆M与圆C1外切、与圆C2内切;④动圆M与圆C1内切、与圆C2外切.在①②情况下,动圆圆心M的轨迹方程为x=0.在③的情况下,设动圆M的半径为r,则|MC1|=r+2,|MC2|=r-2.
故得|MC1|-|MC2|=22.在④的情况下,
同理得|MC2|-|MC1|=22.
由③④得|MC1|-|MC2|=±22.
已知|C1C2|=8,根据双曲线定义,
可知点M的轨迹是以C1(-4,0),C2(4,0)为焦点的双曲线,
且a=2,c=4,b2=c2-a2=14,
其方程为x22-y214=1.
角度2 待定系数法求双曲线的方程
[典例3](1)已知双曲线x2a2-y2b2=1 (a>0,b>0)的虚轴长为2,离心率为52,则其方程是( )
A.x216-y24=1B.x28-y22=1
C.x24-y2=1D.x2-y24=1
解析：选C.由题意,双曲线x2a2-y2b2=1的虚轴长为2,离心率为52,可得b=1,e=ca=52,
即c=52a,因为c2=a2+b2,解得:a=2.
所以双曲线的方程为x24-y2=1.
(2)已知双曲线x2a2-y2b2=1(a>0,b>0)的左焦点为F,离心率为2.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.x24-y24=1B.x28-y28=1
C.x24-y28=1D.x28-y24=1
解析：选B.由离心率为2,可知a=b,c=2a,
所以F(-2a,0),
由题意知kPF=4-00-(-2a)=42a=1,
所以2a=4,解得a=22,
所以双曲线的方程为x28-y28=1.
求双曲线标准方程的方法
(1)定义法.
根据双曲线的定义确定a2,b2的值,再结合焦点位置,求出双曲线方程,常用的关系有:
①c2=a2+b2;
②双曲线上任意一点到双曲线两焦点的距离的差的绝对值等于2a.
(2)待定系数法.
一般步骤.
1.(2023·福州模拟)双曲线C:x2a2-y2b2=1(a>0,b>0)过点(2,3),且离心率为2,则该双曲线的标准方程为( )
A.x2-y23=1B.x23-y2=1
C.y23-x2=1D.y2-x23=1
解析：选A.双曲线离心率e=ca=2,故c=2a,b=3a,
将点(2,3)代入双曲线方程可得,2a2-33a2=1a2=1,
故a=1,b=3,双曲线的方程为x2-y23=1.
2.已知双曲线C:x2a2-y2b2=1 (a>0,b>0) 的右焦点为F,坐标原点为O,在双曲线C的右支上存在两点M,N,使得四边形OMFN是正方形,则( )
A.b2a2-a2b2=4B.1a2-1b2=4
C.a2b2-b2a2=4D.1b2-1a2=4
解析：选A.因为四边形OMFN是正方形,故OF=MN=c,则M点的坐标为c2,c2,
又点M在双曲线C上,
则c24a2-c24b2=1,又a2+b2=c2,
整理得b2a2-a2b2=4.
3.已知双曲线C:x2a2-y2b2=1 (a>0,b>0) 的左、右焦点分别为F1,F2,一条渐近线方程为y=2x,过双曲线C的右焦点F2作倾斜角为π3的直线l交双曲线的右支于A,B两点,若△AF1B的周长为36,则双曲线C的标准方程为( )
A.x22-y24=1B.x24-y22=1
C.x2-y22=1D.x22-y2=1
解析：选C.因为双曲线C:x2a2-y2b2=1 (a>0,b>0) 的一条渐近线方程为y=2x,
所以b=2a,则双曲线方程为x2a2-y22a2=1 (a>0),F1(-3a,0),F2(3a,0),
所以直线l为y=tanπ3(x-3a)=3(x-3a),
设A(x1,y1),B(x2,y2),
由x2a2-y22a2=1y=3(x-3a),得x2-63ax+11a2=0,
则x1+x2=63a,x1x2=11a2,
所以AB=1+3·(x1+x2)2-4x1x2
=2108a2-44a2=16a,
因为AF1=AF2+2a,BF1=BF2+2a,
所以AF1+BF1=AF2+BF2+4a
=AB+4a=20a,
因为△AF1B的周长为36,
所以AF1+BF1+AB=36,
所以20a+16a=36,得a=1,
所以双曲线方程为 x2-y22=1.
【加练备选】
已知双曲线C:x2a2-y2b2=1(a>0,b>0)的顶点分别为A1,A2,以线段A1A2为直径的圆与直线ax+by-2ab=0相切,且双曲线C的焦距为4,则双曲线C的方程为( )
A.x23-y2=1B.x29-y23=1
C.x2-y23=1D.y29-x23=1
解析：选A.由题意知,圆的半径为a,圆心为(0,0).设圆心到直线的距离为d,
则d=|-2ab|a2+b2=a,所以a2=3b2.
因为双曲线的焦距为4,所以c=2,
又c2=a2+b2,解得a=3,b=1,
所以双曲线的方程为x23-y2=1.
双曲线的几何性质
角度1 双曲线的离心率
[典例4](1)(2023·珠海模拟)双曲线C:x2a2-y2b2=1(a>0,b>0)的右支上一点M关于原点O的对称点为点N,F为双曲线的右焦点,若MO=OF,∠FMN=π3,则双曲线C的离心率e为( )
A.2B.3C.2+1D.3+1
解析：选D.设F'为双曲线左焦点,连接MF',NF',NF(图略),OF=12MN,由平面几何知识可知MF⊥NF,根据对称性,四边形MFNF'为矩形,在Rt△MFN中,MN=F'F=2c,所以MF=c,NF=3c,根据双曲线的定义可知MF'-MF=3c-c=2a⇒e=ca=23-1=3+1.
(2)(2022·福州模拟)已知F1,F2分别为双曲线x2a2-y2b2=1(a>0,b>0) 的两个焦点,曲线上的点P到原点的距离为b,且sin∠PF2F1=2sin∠PF1F2,则该双曲线的离心率为 .
解析：设焦距为2c,
因为sin∠PF2F1=2sin∠PF1F2,
12c·PF1sin∠PF1F2
=12c·PF2sin∠PF2F1,
所以PF1=2PF2,又PF1-PF2=2a,
所以PF2=2a,PF1=4a,
因为cs∠POF1=b2+c2-16a22bc,
cs∠POF2=b2+c2-4a22bc,
∠POF1+∠POF2=180°,
所以b2+c2-16a22bc=-b2+c2-4a22bc,
结合b2=c2-a2整理得c2a2=112,
即e=ca=222.
答案:222
求双曲线离心率的方法
(1)若可求得a,c,直接利用e=ca求解;
(2)若已知a,b,可直接利用e=1+(ba) 2得解;
(3)若得到的是关于a,c的齐次方程pc2+qac+ra2=0(p,q,r为常数,且pqr≠0),则转化为关于e的方程pe2+qe+r=0求解.
角度2 与双曲线有关的面积问题
[典例5]金榜原创·易错对对碰
(1)双曲线C:x24-y22=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点.若|PO|=|PF|,则△PFO的面积为( )
A.324B.322C.22D.32
解析：选A.方法一:双曲线x24-y22=1的右焦点F(6,0),一条渐近线的方程为y=22x,不妨设点P在第一象限,由|PO|=|PF|,得点P的横坐标为62,纵坐标为22×62=32,即△PFO的底边长为6,高为32,
所以它的面积为12×6×32=324.
方法二:不妨设点P在第一象限,
根据题意可知c2=6,所以|OF|=6.
又tan∠POF=ba=22,
所以等腰三角形POF的高h=62×22=32,
所以S△PFO=12×6×32=324.
(2)已知F是双曲线C:x24-y25=1的一个焦点,点P在C上,O为坐标原点.若|OP|=|OF|,则△OPF的面积为( )
A.32B.52C.72D.92
解析：选B.由F是双曲线x24-y25=1的一个焦点,
知|OF|=3,所以|OP|=|OF|=3.
不妨设点P在第一象限,P(x0,y0),x0>0,y0>0,
则x02+y02=3,x024-y025=1, 解得x02=569,y02=259,
所以P2143,53,
所以S△OPF=12|OF|·y0=12×3×53=52.
与双曲线有关的面积问题的求解策略
一是确定三角形的底与高(易于计算长度的);
二是分别求出高与底边长度;
三是计算出面积.
角度3 与双曲线渐近线有关的问题
[典例6](1) (2022·临沂模拟)已知双曲线x2a2-y2b2=1 (a>0,b>0)的焦距为45,实轴长为4,则C的渐近线方程为( )
A.y=±2xB.y=±5x
C.y=±12xD.y=±55x
解析：选A.由已知得,双曲线的焦点在x轴上,
双曲线的焦距2c=45,解得c=25,
双曲线的实轴长为2a=4,解得a=2,
则b=c2-a2=20-4=4,
即双曲线C的渐近线方程为 y=±bax=±2x.
(2)(2021·新高考Ⅱ卷)已知双曲线x2a2-y2b2=1(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为 .
解析：因为双曲线x2a2-y2b2=1(a>0,b>0)的离心率为2,所以e=c2a2=a2+b2a2=2,所以b2a2=3,
所以该双曲线的渐近线方程为y=±bax=±3x.
答案:y=±3x
根据双曲线的渐近线方程可设出双曲线方程
(1)渐近线为y=nmx的双曲线方程可设为x2m2-y2n2=λ(λ≠0);
(2)如果两条渐近线的方程为Ax±By=0,那么双曲线的方程可设为A2x2-B2y2=m(m≠0);
(3)与双曲线x2a2-y2b2=1共渐近线的双曲线方程可设为x2a2-y2b2=λ(λ≠0).
1.(2023·汕尾模拟)已知双曲线x2a2-y2b2=1(a>0,b>0)的渐近线方程为y=±3x,则该双曲线的离心率为( )
A.233B.2C.3D.2
解析：选D.双曲线x2a2-y2b2=1(a>0,b>0)的渐近线方程为y=±bax,ba=3,b=3a,离心率e=ca=a2+b2a2=4a2a2=2.
2.已知双曲线 x2a2-y2b2=1(a>0,b>0) 的两条渐近线与直线x=-1围成的三角形的面积为3,则双曲线的离心率为( )
A.6B.3C.23D.2
解析：选D.双曲线的渐近线为y=±bax,
令x=-1,可得y=±ba,
不妨令A(-1,ba),B(-1,-ba),
所以AB=2ba,
所以S△AOB=12AB·xA=3,
所以AB=23,即2ba=23,所以ba=3,
所以e=ca=a2+b2a2=1+ba2=2.
3.(2023·天津模拟)设F1,F2是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,P为双曲线右支上一点,若∠F1PF2=90°,c=2,S△PF2F1=3,则双曲线的两条渐近线的夹角为( )
A.π2B.π4C.π3D.π6
解析：选C.不妨设点P在第一象限,其点的坐标为(x0,y0),由题可知12·y0·2c=3,
所以y0=32,又∠F1PF2=90°,所以|OP|=2,
即x02+y02=4,所以x0=72,
即P(72,32),代入双曲线方程得74a2-94b2=1,a2+b2=4;
解得a2=1,b2=3,或a2=7,b2=-3(舍).
故渐近线的斜率k=±ba=±3.
故双曲线的两条渐近线倾斜角分别为π3与2π3.
故双曲线的两条渐近线的夹角为π3.
4. (多选题)(2022·聊城模拟)已知双曲线C:x29-k+y2k-1=1(0A.双曲线C的焦点在x轴上
B.双曲线C的焦距等于42
C.双曲线C的焦点到其渐近线的距离等于1-k
D.双曲线C的离心率的取值范围为1,103
解析：选ACD.对A:因为0所以9-k>0,k-1<0,
所以双曲线C:x29-k-y21-k=1(0对B:由A知a2=9-k,b2=1-k,
所以c2=a2+b2=10-2k,所以c=10-2k,
所以双曲线C的焦距等于
2c=210-2k(0对C:设焦点在x轴上的双曲线C的方程为
x2a2-y2b2=1(a>0,b>0),
焦点坐标为(±c,0),则渐近线方程为y=±bax,
即bx±ay=0,
所以焦点到渐近线的距离d=bca2+b2=b,
所以双曲线C:x29-k-y21-k=1(0对D:双曲线C的离心率
e=1+b2a2=1+1-k9-k=2-89-k,
因为0所以e=2-89-k∈1,103,故选项D正确.
5.(2023·北京模拟)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,直线l:y=2x-10过双曲线C的一个焦点,并且与双曲线C的一条渐近线平行,则双曲线C的方程为 ;若点M(-10,25),则|MF1|-|MF2|的值为 .
解析：在直线l的方程中,令y=0可得x=5,则c=5,
由于直线l:y=2x-10与双曲线C的一条渐近线平行,则ba=2c=a2+b2=5,解得a=5b=25 ,
因此,双曲线C的方程为x25-y220=1;
因为(-10)25-(25)220=1,
所以点M在双曲线C的左支上,
故|MF1|-|MF2|=-2a=-25.
答案:x25-y220=1 -25
【加练备选】
已知双曲线y2+x2m=1的渐近线方程为y=±33x,则m= .
解析：因为双曲线y2+x2m=1,所以m<0,即双曲线的标准方程为y2-x2-m=1,
则a=1,b=-m,又双曲线y2+x2m=1的渐近线方程为y=±33x,
所以ab=33,即1-m=33,
解得m=-3.
答案:-3
标准
方程
x2a2-y2b2=1
(a>0,b>0)
y2a2-x2b2=1
(a>0,b>0)
图形
性
质
范围
x≤-a或
x≥a,y∈R
y≤-a或
y≥a,x∈R
对称性
对称轴:坐标轴 对称中心:原点
顶点
顶点坐标:
A1(-a,0),
A2(a,0)
顶点坐标:
A1(0,-a),
A2(0,a)
渐近线
y=±bax
y=±abx
性
质
离心率
e=ca,e∈(1,+∞)
a,b,c
的关系
c2=a2+b2
实虚
轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;
线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;
a叫做双曲线的实半轴长,b叫做双曲线的虚半轴长
等轴
双曲线
①定义:中心在原点,以坐标轴为对称轴,实半轴长与虚半轴长相等的双曲线叫做等轴双曲线.
②性质:a=b;e=2;渐近线互相垂直;等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项
教材改编
结论应用
易错易混
1,5
3,4
2