高考数学第一轮复习复习第7节　空间距离及立体几何中的探索性问题（讲义）

这是一份高考数学第一轮复习复习第7节　空间距离及立体几何中的探索性问题（讲义），共34页。

1.会求空间中两点的距离、点到直线的距离、点到平面的距离.
2.以空间向量为工具,探究空间几何体中线、面的位置关系或空间角存在的条件.
1.两点的距离
(1)利用A,B两点间的距离为|AB→|,结合向量的模和数量积求解.
(2)设点A(x1,y1,z1),B(x2,y2,z2),则|AB→|=(x1-x2)2+(y1-y2)2+(z1-z2)2.
2.点到直线的距离
如图,已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点,设AP→=a,则向量AP→在直线l上的投影向量AQ→=(a·u)u.在Rt△APQ中,由勾股定理,得
PQ=|AP→|2-|AQ→|2=a2-(a·u)2.
3.点到平面的距离
如图,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.过点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P到平面α的距离就是AP→在直线l上的投影向量 QP→的长度,因此PQ=|AP→·n|n||=|AP→·n|n||=|AP→·n||n|.
1.已知平面α的一个法向量为n=(-2,-2,1),点A(-1,3,0)在平面α内,则点P(-2,1,4)到平面α的距离为( D )
A.10B.3C.83D.103
解析:PA→=(1,2,-4),点P到平面α的距离d=|PA→·n||n|=|-2-4-4|4+4+1=103.
2.已知A(0,0,2),B(1,0,2),C(0,2,0),则点A到直线BC的距离为( A )
A.223B.1C.2D.22
解析:因为A(0,0,2),B(1,0,2),C(0,2,0),
所以AB→=(1,0,0),BC→=(-1,2,-2),
所以点A到直线BC的距离为
d=|AB→|1-(cs)2
=|AB→|1-(AB→·BC→|AB→||BC→|) 2
=1×1-(-11×3) 2=223.
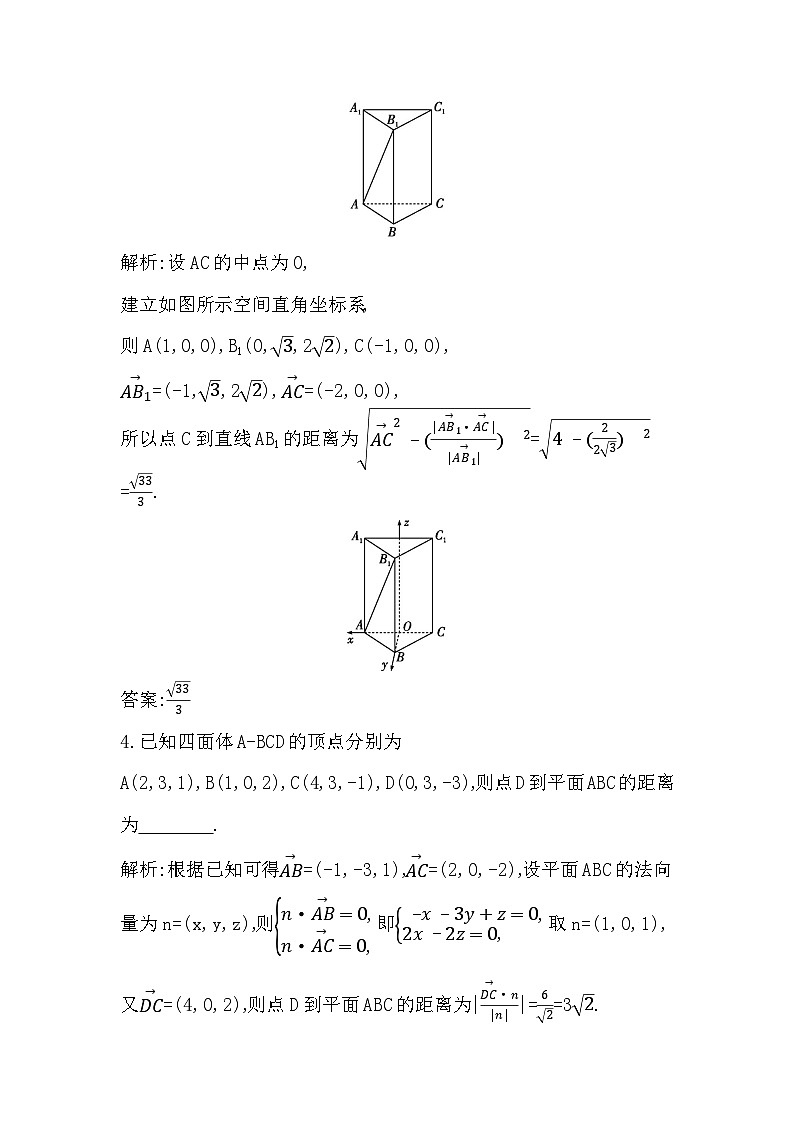
3.(2022·辽宁大连三模)如图,在正三棱柱ABC-A1B1C1中,若BB1=22,AB=2,则点C到直线AB1的距离为 .
解析:设AC的中点为O,
建立如图所示空间直角坐标系,
则A(1,0,0),B1(0,3,22),C(-1,0,0),
AB1→=(-1,3,22),AC→=(-2,0,0),
所以点C到直线AB1的距离为AC→2-(|AB1→·AC→||AB1→|) 2=4-(223) 2=333.
答案:333
4.已知四面体A-BCD的顶点分别为A(2,3,1),B(1,0,2),C(4,3,-1),D(0,3,-3),则点D到平面ABC的距离为 .
解析:根据已知可得AB→=(-1,-3,1),AC→=(2,0,-2),设平面ABC的法向量为n=(x,y,z),则n·AB→=0,n·AC→=0,即-x-3y+z=0,2x-2z=0,取n=(1,0,1),
又DC→=(4,0,2),则点D到平面ABC的距离为|DC→·n|n||=62=32.
答案:32
空间距离
1.已知空间直角坐标系Oxyz中有一点A(-1,-1,2),点B是平面xOy内的直线x+y=1上的动点,则A,B两点间的最短距离是( B )
A.6B.342C.3D.172
解析:因为点B是平面xOy内的直线x+y=1上的动点,
所以可设点B(m,1-m,0),由空间两点之间的距离公式得,
|AB|=(-1-m)2+[-1-(1-m)]2+(2-0)2=2m2-2m+9=2(m-12) 2+172,
所以当m=12时,|AB|的最小值为172=342,即A,B两点间的最短距离是342.
2.已知棱长为1的正方体ABCD-EFGH,若点P在正方体内部且满足AP→=34AB→+12AD→+23AE→,则点P到AB的距离为( A )
A.56B.18112
C.10306D.56
解析:建立如图所示的空间直角坐标系,
则AP→=34(1,0,0)+12(0,1,0)+23(0,0,1)=(34,12,23).又AB→=(1,0,0),
所以AP→在AB→上的投影为|AP→·AB→||AB→|=34,
所以点P到AB的距离为|AP→|2-(|AP→·AB→||AB→|) 2=56.
3.如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点,则点D到平面PEF的距离为 ,直线AC到平面PEF的距离为 .
解析:建立如图所示的空间直角坐标系,则D(0,0,0),P(0,0,1),A(1,0,0),C(0,1,0),E(1,12,0),F(12,1,0),PE→=(1,12,-1),PF→=(12,1,-1),AP→=(-1,0,1),DP→=(0,0,1).
设平面PEF的法向量为n=(x,y,z),
则n·PE→=0,n·PF→=0,即x+12y-z=0,12x+y-z=0,
解得x=y,令x=y=2,得n=(2,2,3),
因此,点D到平面PEF的距离为|DP→·n||n|=317=31717.
因为E,F分别为AB,BC的中点,
所以EF∥AC,又EF⊂平面PEF,
所以AC∥平面PEF,
所以直线AC到平面PEF的距离为|AP→·n||n|=117=1717.
答案:31717 1717
4.在棱长为3的正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点,则平面ADE与平面B1C1F之间的距离为 .
解析:以点A为坐标原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,连接AB1,
则A(0,0,0),D(0,3,0),E(3,0,32),B1(3,0,3),C1(3,3,3),F(0,3,32),
AD→=(0,3,0),B1C1→=(0,3,0),则AD→=B1C1→,
因为AD,B1C1不在同一条直线上,则AD∥B1C1,
因为AD⊄平面B1C1F,B1C1⊂平面B1C1F,
则AD∥平面B1C1F,
同理可证,AE∥平面B1C1F,AD∩AE=A,AD,AE⊂平面ADE,
故平面ADE∥平面B1C1F,
设平面ADE的法向量为n=(x,y,z),AD→=(0,3,0),AE→=(3,0,32),
由n·AD→=3y=0,n·AE→=3x+32z=0,取x=1,
可得n=(1,0,-2),
又因为AB1→=(3,0,3),因此,平面ADE与平面B1C1F之间的距离为d=|AB1→·n||n|=35=355.
答案:355
(1)当一条直线和一个平面平行时,直线上的各点到平面的距离相等,当两个平面平行时,一个平面上的各点到另一个平面的距离相等,由此可知,这两种距离都是转化为点面距离.
(2)异面直线间的距离
设向量n与两异面直线a,b都垂直,M∈a,P∈b,则两异面直线a,b间的距离d就是MP→在向量n方向上投影的绝对值,即d=|n·MP→||n|.
立体几何中的探索性问题
以平行为背景的存在判断型问题
[例1] 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的 2 倍,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-S的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SC∶SE的值;若不存在,试说明理由.
(1)证明:连接BD交AC于点O,连接SO,由题意知SO⊥AC,
在正方形ABCD中,BD⊥AC,
又BD∩SO=O,BD,SO⊂平面SBD,
所以AC⊥平面SBD,
又SD⊂平面SBD,所以AC⊥SD.
(2)解:由题知SO⊥平面ABCD,以O为坐标原点,OB,OC,OS所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
设底面边长为a,则高SO=62a,则S(0,0,62a),D(-22a,0,0),C(0,22a,0),B(22a,0,0),
又SD⊥平面PAC,则平面PAC的一个法向量为DS→=(22a,0,62a),
平面SAC的一个法向量为OD→=(-22a,0,0),
则|cs|=|DS→·OD→||DS→||OD→|=a2222a·2a=12,
又二面角P-AC-S为锐角,则二面角P-AC-S的大小为π3.
(3)解:在棱SC上存在一点E,使得BE∥平面PAC,
由(2)知平面PAC的一个法向量DS→=(22a,0,62a),
又CS→=(0,-22a,62a),BC→=(-22a,22a,0),
设CE→=tCS→,t∈[0,1],则BE→=BC→+CE→=BC→+tCS→=(-22a,22a(1-t),62at),
因为BE∥平面PAC,所以BE→·DS→=0,
所以-12a2+32a2t=0,解得t=13.
故当SC∶SE=3∶2时,BE∥平面PAC.
以垂直为背景的存在判断型问题
[例2] 如图所示,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,圆台下底面的圆心O为AB的中点,直径为2,圆与直线AB交于E,F,圆台上底面的圆心O1在A1B1上,直径为1.
(1)求A1C与平面A1ED所成角的正弦值;
(2)求二面角E-A1D-F的余弦值;
(3)圆台上底圆周上是否存在一点P,使得FP⊥AC1?若存在,求点P到直线A1B1的距离;若不存在,请说明理由.
解:(1)由题意可知,建立空间直角坐标系如图所示,
则A1(2,0,2),C(0,4,0),E(2,1,0),D(0,0,0),
所以A1C→=(-2,4,-2),DA1→=(2,0,2),DE→=(2,1,0),
设平面A1ED的法向量为n=(x,y,z),
则有n·DA1→=0,n·DE→=0,即2x+2z=0,2x+y=0,
令x=1,则y=-2,z=-1,故n=(1,-2,-1),
所以|cs|=|A1C→·n||A1C→||n|=23,
故A1C与平面A1ED所成角的正弦值为23.
(2)由(1)可知,F(2,3,0),DA1→=(2,0,2),所以DF→=(2,3,0),
设平面A1DF的法向量为m=(a,b,c),
则有m·DA1→=0,m·DF→=0,即2a+2c=0,2a+3b=0,
令a=3,则b=-2,c=-3,故m=(3,-2,-3),
所以|cs|=|n·m||n||m|=53333.
故二面角E-A1D-F的余弦值为53333.
(3)由(1)可知,A(2,0,0),C1(0,4,2),F(2,3,0),
所以AC1→=(-2,4,2),
假设存在这样的点P,设P(x,y,2),
由题意可知(x-2)2+(y-2)2=14,
所以FP→=(x-2,y-3,2),因为FP⊥AC1,
则有FP→·AC1→=-2(x-2)+4(y-3)+4=0,
所以x=2y-2,又(x-2)2+(y-2)2=14,
所以5y2-20y+794=0,
解得x=2-55,y=2-510或x=2+55,y=2+510,
所以当P(2+55,2+510,2)或(2-55,2-510,2)时,FP⊥AC1,
此时点P到直线A1B1的距离为55.
以空间角为背景的探索性问题
[例3] 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.
(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角为π6,请问在线段A1C上是否存在点E,使得二面角A-BE-C的大小为2π3?若存在,请求出E的位置;若不存在,请说明理由.
(1)证明:连接AB1交A1B于点D,
因为AA1=AB,则AD⊥A1B,
由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,AD⊂侧面A1ABB1,
得AD⊥平面A1BC,又BC⊂平面A1BC,所以AD⊥BC.
三棱柱ABC-A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB⊂侧面A1ABB1,故AB⊥BC.
(2)解:连接CD,由(1)知,AD⊥平面A1BC,则∠ACD为直线AC与平面A1BC所成的角,
所以∠ACD=π6,因为AA1=AB=2,所以AD=2,所以AC=22,BC=2.
假设在线段A1C上存在一点E,使得二面角A-BE-C的大小为2π3,
由三棱柱ABC-A1B1C1是直三棱柱,所以以点A为原点,以AC,AA1所在直线分别为y轴、z轴,以过A点和AC垂直的直线为x轴,建立空间直角坐标系,
如图所示,则A1(0,0,2),C(0,22,0),B(2,2,0),B1(2,2,2),
且设A1E→=λA1C→(0≤λ<1),
A1C→=(0,22,-2),
得E(0,22λ,2-2λ),
所以AE→=(0,22λ,2-2λ),AB→=(2,2,0).
设平面EAB的法向量为n1=(x,y,z),
由AE→⊥n1,AB→⊥n1得22λy+(2-2λ)z=0,2x+2y=0,
取n1=(1,-1,2λ1-λ),
由(1)知AB1⊥平面A1BC,所以平面CEB的一个法向量为AB1→=(2,2,2),
所以|cs2π3|=|AB1·n1||AB1||n1|=|22λ||1-λ|22×2+(2λ1-λ) 2=12,解得λ=12,
所以点E为线段A1C的中点时,二面角A-BE-C的大小为2π3.
(1)对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.
(2)对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.
[针对训练]
1.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AB∥CD,AB=AD=PA=2CD=4,G为PD的中点.
(1)求证:AG⊥平面PCD;
(2)若点F为PB的中点,线段PC上是否存在一点H,使得平面GHF⊥平面PCD?若存在,请确定H的位置;若不存在,请说明理由.
(1)证明:因为PA⊥平面ABCD,所以PA⊥AB,又AD⊥AB,AD∩PA=A,所以AB⊥平面PAD,又AB∥CD,所以CD⊥平面PAD,AG⊂平面PAD,CD⊥AG.
又PA=AD,G为PD的中点,所以AG⊥PD,而PD∩DC=D,所以AG⊥平面PCD.
(2)解:假设线段PC上存在一点H满足题意,以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图,则A(0,0,0),B(0,4,0),C(4,2,0),D(4,0,0),P(0,0,4),F(0,2,2),G(2,0,2).
所以PC→=(4,2,-4),设PH→=kPC→(0≤k≤1),
所以PH→=(4k,2k,-4k),则H(4k,2k,-4k+4),
所以GH→=(4k-2,2k,-4k+2),FG→=(2,-2,0),
设平面GHF的法向量为n=(x,y,z),
则n·GH→=0,n·FG→=0,
即(4k-2)x+2ky+(-4k+2)z=0,2x-2y=0,令x=2k-1,则n=(2k-1,2k-1,3k-1),
由(1)可知AG→=(2,0,2)为平面PCD的一个法向量,若平面GHF⊥平面PCD,则n·AG→=0,
即2k-1+3k-1=0,解得k=25.
即当PH=25PC时,平面GHF⊥平面PCD.
2.如图①为某凉亭的实景效果图,图②为设计图,该凉亭的支撑柱高AA1为33 m,顶部为底面边长为2 m的正六棱锥,且侧面与底面所成的角都是45°.
(1)求该凉亭及其内部所占空间的大小;
(2)在直线PC上是否存在点M,使得直线MA与平面BD1F1所成角的正弦值为33?若存在,请确定点M的位置;若不存在,请说明理由.
解:(1)由题意,得凉亭的顶是正六棱锥,侧面与水平面成45°角,
取A1F1的中点G,连接O1G,PG,则O1G⊥A1F1,PG⊥A1F1,
故∠PGO1=45°,易求O1G=3,所以PO1=3,
所以该凉亭的体积分为两部分,上半部分为正六棱锥,其体积为V1=13×6×34×22×3=6 (m3),
下半部分为正六棱柱,其体积为V2=6×34×22×33=54(m3),所以该凉亭及内部所占空间为60 m3.
(2)假设在直线PC上存在点M,使得直线MA与平面BD1F1所成角的正弦值为33.取AB的中点H,以OH,OC,OP所在直线分别为x轴、y轴、z轴,以点O为坐标原点,建立空间直角坐标系,如图所示.
则A(3,-1,0),B(3,1,0),D1(-3,1,33),F1(0,-2,33),P(0,0,43),C(0,2,0),
设PM→=tPC→=(0,2t,-43t),
则M(0,2t,43-43t),设平面BD1F1的法向量为n=(x,y,z),
AM→=(-3,2t+1,43(1-t)),BD1→=(-23,0,33),BF1→=(-3,-3,33),
则BD1→·n=0,BF1→·n=0,即-23x+33z=0,-3x-3y+33z=0,
令x=3,解得y=3,z=2,
所以平面BD1F1的一个法向量为n=(3,3,2),
设直线MA与平面BD1F1所成的角为θ,则sin θ=|-33+3(2t+1)+83(1-t)|9+3+4·3+(2t+1)2+[43(1-t)]2=33,
化简得127t2-206t+127=0,Δ=(-206)2-4×1272=2062-2542<0,故该方程不存在实数解,
所以在直线PC上不存在点M,使得直线MA与平面BD1F1所成角的正弦值为33.
[例1] (多选题)(2021·新高考Ⅰ卷)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足BP→=λBC→+μBB1→,其中λ∈[0,1],μ∈[0,1],则( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值
C.当λ=12时,有且仅有一个点P,使得A1P⊥BP
D.当μ=12时,有且仅有一个点P,使得A1B⊥平面AB1P
解析:BP→=λBC→+μBB1→(0≤λ≤1,0≤μ≤1).
对于选项A,当λ=1时,点P在棱CC1上运动,如图(1)所示,此时△AB1P的周长为AB1+AP+PB1=2+1+μ2+1+(1-μ)2=2+1+μ2+2-2μ+μ2,不是定值,故A错误;
对于选项B,当μ=1时,点P在棱B1C1上运动,如图(2)所示,
则VP−A1BC=VA1−PBC=13S△PBC×32=36S△PBC=36×12×1×1=312,为定值,故B正确;
对于选项C,取BC的中点D,B1C1的中点D1,连接DD1,A1B(图略),则当λ=12时,点P在线段DD1上运动,假设A1P⊥BP,则A1P2+BP2=A1B2,即(32)2+(1-μ)2+(12)2+μ2=2,解得μ=0或μ=1,所以点P与点D或D1重合时,A1P⊥BP,故C错误;
法一 由多选题特征,排除A,C.故选BD.
法二 对于选项D,易知四边形ABB1A1为正方形,所以A1B⊥AB1,设AB1与A1B交于点K,连接PK(图略),要使A1B⊥平面AB1P,需A1B⊥KP,所以点P只能是棱CC1的中点,故选项D正确.故选BD.
法三 对于选项D,分别取BB1,CC1的中点E,F,连接EF,则当μ=12时,点P在线段EF上运动,以点C1为原点建立如图(3)所示的空间直角坐标系,则B(0,1,1),B1(0,1,0),A1(32,12,0),P(0,1-λ,12),所以A1B→=(-32,12,1),B1P→=(0,-λ,12),若A1B⊥平面AB1P,则A1B⊥B1P,所以-λ2+12=0,解得λ=1,所以只存在一个点P,使得A1B⊥平面AB1P,此时点P与F重合,故D正确.故选BD.
[例2] 如图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E使得二面角A-DE-P为直二面角,并说明理由.
法一 (1)证明:因为PA⊥底面ABC,BC⊂底面ABC,所以PA⊥BC,
又∠BCA=90°,所以AC⊥BC.
又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.
(2)解:因为D为PB的中点,DE∥BC,
所以DE=12BC.
又由(1)知,BC⊥平面PAC,
所以DE⊥平面PAC,垂足为点E.
所以∠DAE是AD与平面PAC所成的角.
因为PA⊥底面ABC,AB⊂底面ABC,
所以PA⊥AB.
又PA=AB,
所以△ABP为等腰直角三角形.
所以AD=12AB.
在Rt△ABC中,∠ABC=60°.
所以BC=12AB.
所以在Rt△ADE中,
sin∠DAE=DEAD=BC2AD=24,
所以cs∠DAE=144.
(3)解:存在.
理由如下:因为DE∥BC,
又由(1)知,BC⊥平面PAC,
所以DE⊥平面PAC.
又因为AE⊂平面PAC,PE⊂平面PAC,
所以DE⊥AE,DE⊥PE.
所以∠AEP为二面角A-DE-P的平面角.
因为PA⊥底面ABC,AC⊂底面ABC,
所以PA⊥AC,
所以∠PAC=90°,
所以在棱PC上存在一点E,使得AE⊥PC,
即∠AEP=90°,
故存在点E使得二面角A-DE-P是直二面角.
法二 如图所示,以A为原点,过点A平行于BC的直线为x轴,AC所在直线为y轴,AP所在直线为z轴建立空间直角坐标系.
设AP=a,由已知可得A(0,0,0),B(-12a,32a,0),C(0,32a,0),P(0,0,a).
(1)证明:因为AP→=(0,0,a),BC→=(12a,0,0),
所以BC→·AP→=0,所以BC⊥AP.
因为∠BCA=90°,所以BC⊥AC.
又AP∩AC=A,AP⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.
(2)解:因为D为PB的中点,DE∥BC,
所以E为PC的中点.
所以D(-14a,34a,12a),E(0,34a,12a).
又由(1)知,BC⊥平面PAC,
所以DE⊥平面PAC,垂足为点E,
所以∠DAE是AD与平面PAC所成的角.因为AD→=(-14a,34a,12a),AE→=(0,34a,12a),
所以cs∠DAE=AD→·AE→|AD→||AE→|=144.
(3)解:同法一.
[例3] 如图,P为圆锥的顶点,O是圆锥底面的圆心,AC为底面直径,△ABD为底面圆O的内接正三角形,且边长为3,E在母线PC上,且AE=3,CE=1,EC⊥BD.
(1)求证:平面BED⊥平面ABD;
(2)设线段PO上动点为M,求直线DM与平面ABE所成角的正弦值的最大值.
(1)证明:如图,设AC交BD于点F,连接EF,
易知PO⊥BD,
又EC⊥BD,EC∩PO=P,EC,PO⊂平面AEC,所以BD⊥平面AEC,
又EF⊂平面AEC,所以EF⊥BD.
又△ABD是底面圆的内接正三角形,
由AD=3,可得AF=32,AC=2.
又AE=3,CE=1,
所以AC2=AE2+CE2,即∠AEC=90°.
又AEAC=AFAE=32,所以△ACE∽△AEF,
所以∠AFE=∠AEC=90°,即EF⊥AC.
又AC,BD⊂平面ABD,AC∩BD=F,
所以EF⊥平面ABD.
又EF⊂平面BED,所以平面BED⊥平面ABD.
(2)解:易知PO=2EF=3.以点F为坐标原点,FA,FB,FE所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(32,0,0),B(0,32,0),D(0,-32,0),E(0,0,32),P(12,0,3),O(12,0,0),
所以AB→=(-32,32,0),AE→=(-32,0,32),DO→=(12,32,0),OP→=(0,0,3),
设平面ABE的法向量为n=(x,y,z),
则AB→·n=0,AE→·n=0,即-3x+y=0,-3x+z=0,令x=1,则n=(1,3,3).设OM→=λOP→(0≤λ≤1),
可得DM→=DO→+OM→=(12,32,3λ).
设直线DM与平面ABE所成的角为θ,
则sin θ=|n·DM→||n|·|DM→|=|3λ+2|7×3λ2+1 .
令y=12x+13x2+1,x∈[0,1],则y=12x+13x2+1=4(x+112x2+13)
=4[x+112(x+112-112) 2+13]=4x+112+49144x+112-16≤42·(x+112)·(49144x+112)-16=4,
当且仅当x=12时,等号成立,
所以当x=12时,y=12x+13x2+1有最大值4,
于是当λ=12时,sin2θ=9λ2+12λ+47(3λ2+1)=17(3+12λ+13λ2+1)有最大值为1,所以sin θ的最大值为1,
故直线DM与平面ABE所成角的正弦值的最大值为1.
[选题明细表]
1.如图,已知正方体ABCDA1B1C1D1的棱长为2,E是线段AB的中点.
(1)证明:BD⊥平面AA1C1C;
(2)若P是线段BC上的动点,求点P到平面B1DE的距离的取值范围.
(1)证明:因为四边形ABCD是正方形,
所以BD⊥AC,
因为AA1⊥平面ABCD,BD⊂平面ABCD,
所以AA1⊥BD,
因为AC∩AA1=A,AC,AA1⊂平面AA1C1C,
所以BD⊥平面AA1C1C.
(2)解:以D为坐标原点,分别以DA,DC,DD1所在直线为x轴、y轴、
z轴建立空间直角坐标系,
则D(0,0,0),E(2,1,0),B1(2,2,2),
设P(a,2,0)(0≤a≤2),
则DP→=(a,2,0),DE→=(2,1,0),DB1→=(2,2,2),
设平面B1DE的法向量为n=(x,y,z),
由DE→·n=0,DB1→·n=0,
则2x+y=0,2x+2y+2z=0,
令x=1,则y=-2,z=1,则n=(1,-2,1).
设点P到平面B1DE的距离为h,
所以h=|DP→·n||n|=|a-4|6=66(4-a)∈[63,263],
所以点P到平面B1DE的距离的取值范围是[63,263].
2.如图,在三棱柱ABCA1B1C1中,AA1⊥底面ABC,AB⊥BC,AB=1,BC=2,
AA1=3.
(1)求直线A1C与AB1所成角的余弦值;
(2)设M为AC的中点,在平面BCC1内找一点N,使得MN⊥平面A1BC,
求点N到平面ABC和平面ABB1的距离.
解:(1)根据题设可知AB,BC,BB1两两垂直,以B为坐标原点,分别以BA,
BC,BB1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则B(0,0,0),A(1,0,0),B1(0,0,3),A1(1,0,3),C(0,2,0),
所以AB1→=(-1,0,3),A1C→=(-1,2,-3),
所以cs =AB1→·A1C→|AB1→||A1C→|=1-32×8=-24,
所以直线A1C与AB1所成角的余弦值为24.
(2)由条件知M(12,1,0).因为点N在平面BCC1内,可设其坐标为N(0,a,b),
则MN→=(-12,a-1,b).
因为MN⊥平面A1BC,
所以MN⊥BC,MN⊥BA1,
由(1)可得BC→=(0,2,0),BA1→=(1,0,3),
所以MN→·BC→=2(a-1)=0,MN→·BA1→=-12+3b=0,
解得a=1,b=36,
所以点N(0,1,36),其到平面ABC的距离为36,到平面ABB1的距离为1.
3.如图,在四棱锥PABCD中,底面ABCD是边长为2的正方形,PB⊥BC,
PD⊥CD,且PA=2,E为PD的中点.
(1)求证:PA⊥平面ABCD;
(2)求直线PC与平面ACE所成角的正弦值;
(3)在线段BC上是否存在点F,使得点E到平面PAF的距离为255?若存在,确定点F的位置;若不存在,请说明理由.
(1)证明:因为四边形ABCD为正方形,
则BC⊥AB,CD⊥AD,
因为PB⊥BC,BC⊥AB,PB∩AB=B,PB,AB⊂平面PAB,所以BC⊥平面PAB.
因为PA⊂平面PAB,所以PA⊥BC.
因为PD⊥CD,CD⊥AD,PD∩AD=D,
PD,AD⊂平面PAD.
所以CD⊥平面PAD.
因为PA⊂平面PAD,
所以PA⊥CD,
因为BC∩CD=C,BC,CD⊂平面ABCD,
所以PA⊥平面ABCD.
(2)解:因为PA⊥平面ABCD,AB⊥AD,以点A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),C(2,2,0),P(0,0,2),E(0,1,1),
设平面ACE的法向量为m=(x,y,z),
则AC→=(2,2,0),AE→=(0,1,1),PC→=(2,2,-2),
由m·AC→=2x+2y=0,m·AE→=y+z=0,
取y=1,可得m=(-1,1,-1),
cs=m·PC→|m||PC→|=23×23=13,
所以直线PC与平面ACE所成角的正弦值为13.
(3)解:设点F(2,t,0)(0≤t≤2),设平面PAF的法向量为n=(a,b,c),
AF→=(2,t,0),AP→=(0,0,2),
由n·AF→=2a+tb=0,n·AP→=2c=0,
取a=t,则n=(t,-2,0),
所以点E到平面PAF的距离为d=|AE→·n||n|=2t2+4=255,因为0≤t≤2,
所以t=1.因此,当点F为线段BC的中点时,点E到平面PAF的距离为255.
4.(2022·江苏苏州调研)如图,在直三棱柱ABCA1B1C1中,△ABC是以BC为斜边的等腰直角三角形,AA1=AB,点D,E分别为棱BC,B1C1上的点,且BDBC=C1EC1B1=t(0(1)若t=12,求证:AD∥平面A1EB;
(2)若二面角C1ADC的大小为π3,求实数t的值.
(1)证明:当t=12时,BDBC=C1EC1B1=t=12,即点D,E分别为BC,B1C1的中点,
在直三棱柱ABCA1B1C1中,AA1BB1,
所以四边形BB1A1A为平行四边形,
连接DE,则DEBB1,
所以DEAA1,
所以四边形DEA1A是平行四边形,
所以AD∥A1E.
又因为AD⊄平面A1EB,A1E⊂平面A1EB,
所以AD∥平面A1EB.
(2)解:AA1⊥平面ABC,又∠BAC=90°,
以AB,AC,AA1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
设AB=AC=AA1=3,
则点A(0,0,0),B(3,0,0),C(0,3,0),C1(0,3,3),
所以AC1→=(0,3,3),BC→=(-3,3,0),AB→=(3,0,0),BD→=tBC→=(-3t,3t,0),
所以AD→=AB→+BD→=(3-3t,3t,0).
设平面AC1D的法向量为n1=(x,y,z),
则n1·AC1→=0,n1·AD→=0,即3y+3z=0,3(1-t)x+3ty=0,
取n1=(t,t-1,1-t),
又平面ADC的一个法向量为n2=(0,0,1),
因为二面角C1ADC的大小为π3,
所以|n1·n2|n1||n2||=csπ3=12,
即1-t3t2-4t+2=12,
得t2-4t+2=0,
又因为05.如图,在四棱锥PABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,
AB=1,PA=2,E为PB的中点,点F在棱PC上,且PF→=λPC→(λ∈[0,1]).
(1)求直线CE与直线PD所成角的余弦值;
(2)当直线BF与平面CDE所成的角最大时,求此时λ的值.
解:(1)如图,以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则C(1,1,0),P(0,0,2),D(1,0,0),B(0,1,0),E(0,12,1),CE→=(-1,-12,1),
PD→=(1,0,-2),
所以cs=CE→·PD→|CE→|·|PD→|=-1-294×5=-255,
所以CE与PD所成角的余弦值为255.
(2)点F在棱PC上,且PF→=λPC→,
所以F(λ,λ,2-2λ),BF→=(λ,λ-1,2-2λ),
又CD→=(0,-1,0),CE→=(-1,-12,1).
设n=(x,y,z)为平面CDE的法向量,
则n·CD→=-y=0,n·CE→=-x-12y+z=0,
取x=1,得n=(1,0,1),
设直线BF与平面CDE所成的角为θ,
则sin θ=2-λλ2+(λ-1)2+(2-2λ)2·2=2-λ2·6λ2-10λ+5(λ∈[0,1]),
令t=2-λ,则t∈[1,2],
所以sin θ=t2·6t2-14t+9=22·19t2-14t+6,
当1t=79,即t=97∈[1,2]时,9t2-14t+6有最小值59,此时sin θ取得最大值为31010,
即BF与平面CDE所成的角最大,此时λ=2-t=2-97=57,即λ的值为57.
6.如图1,在菱形ABCD中,∠ABC=120°,动点E,F在边AD,AB上(不含端点),且存在实数λ使FE→=λBD→(0<λ<1),沿EF将△AEF向上折起得到△PEF,使得平面PEF⊥平面BCDEF,如图2所示.
(1)若BF⊥PD,设三棱锥PBCD和四棱锥PBDEF的体积分别为V1,V2,求V1V2;
(2)试讨论,当点E的位置变化时,二面角EPFB是否为定值?若是,
求出该二面角的余弦值,若不是,说明理由.
解:(1)取EF的中点为G,连接PG,
因为FE→=λBD→(0<λ<1),即EF∥BD,
所以PE=PF,
所以PG⊥EF,又因为平面PEF⊥平面BCDEF,
平面PEF∩平面BCDEF=EF,
所以PG⊥平面BCDEF,
连接GC,由题意可知GC⊥EF,
以点G为坐标原点,分别以GF,GC,GP为x轴、y轴、z轴建立空间直角坐标系,
设BC=2,则F(λ,0,0),B(1,3(1-λ),0),P(0,0,3λ),D(-1,3(1-λ),0),
所以FB→=(1-λ,3(1-λ),0),DP→=(1,-3(1-λ),3λ),
因为BF⊥PD,所以DP→·FB→=(1,-3(1-λ),3λ)·(1-λ,3(1-λ),0)
=1-λ-3(1-λ)2=0,
解得λ=23或λ=1(舍去).
因为三棱锥PBCD和四棱锥PBDEF的体积分别为V1,V2,
所以V1V2=S△BCDS四边形BDEF=S△ABDS四边形BDEF=95.
(2)二面角EPFB是定值.
由(1)知,平面EPF的一个法向量为n1=(0,1,0),
由FB→=(1-λ,3(1-λ),0),FP→=(-λ,0,3λ),
设平面PFB的法向量为n2=(x,y,z),
所以n2·FB→=0,n2·FP→=0⇒(1-λ)x+3(1-λ)y=0,-λx+3λz=0,
取y=1,则x=-3,z=-1,
即n2=(-3,1,-1),
设二面角EPFB的平面角为θ,
所以|cs θ|=|n1·n2|n1|·|n2||=|1|1×5=55,
由图可知二面角EPFB的平面角为钝角,
所以二面角EPFB为定值,其余弦值为-55.知识点、方法
题号
距离综合问题
1
位置关系探索问题
2,3
空间角的探索问题
4,5,6