高考数学第一轮复习复习第5节　解三角形的综合应用（讲义）

这是一份高考数学第一轮复习复习第5节　解三角形的综合应用（讲义），共23页。

能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
测量中的几个有关术语
1.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图),要测量A,B两点间的距离,测量人员在岸边定出基线BC,测得BC=50 m,∠ABC=105°,∠BCA=45°.则可以计算出A,B两点的距离为( D )
A.202 mB.302 mC.402 mD.502 m
解析:由题意,∠BAC=180°-∠ACB-∠ABC=30°,由正弦定理得ABsin∠ACB=BCsin∠BAC⇒AB22=5012⇒AB=502.
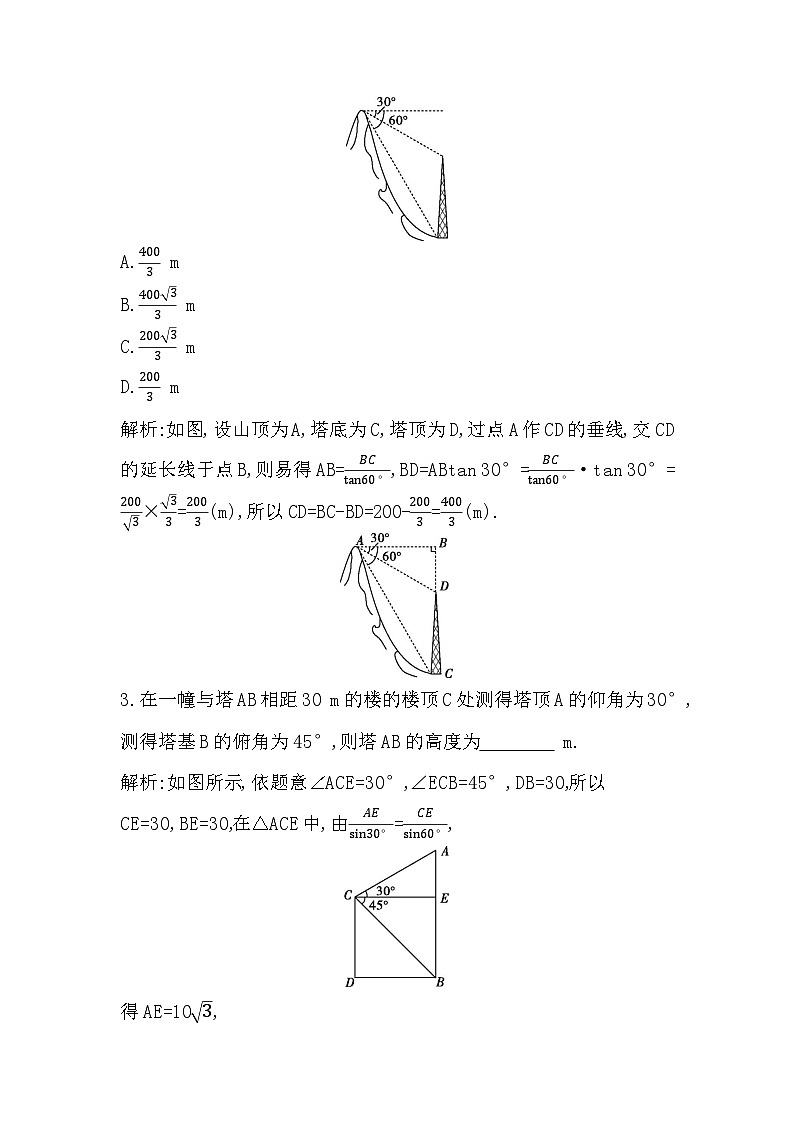
2.如图,在200 m高的山顶上,测得山下一塔顶与塔底的俯角分别是30°,60°,则塔高为( A )
A.4003 m
B.40033 m
C.20033 m
D.2003 m
解析:如图,设山顶为A,塔底为C,塔顶为D,过点A作CD的垂线,交CD的延长线于点B,则易得AB=BCtan60°,BD=ABtan 30°=BCtan60°·tan 30°=2003×33=2003(m),所以CD=BC-BD=200-2003=4003(m).
3.在一幢与塔AB相距30 m的楼的楼顶C处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,则塔AB的高度为 m.
解析:如图所示,依题意∠ACE=30°,∠ECB=45°,DB=30,所以CE=30,BE=30,在△ACE中,由AEsin30°=CEsin60°,
得AE=103,
所以AB=(30+103) m.
答案:30+103
4.海上有A,B,C三个小岛,A,B相距53 km,从A岛望C和B成45°视角,从B岛望C和A成75°视角,则B,C两岛间的距离是 km.
解析:由题意可知∠ACB=60°,
由正弦定理得ABsin∠ACB=BCsin∠BAC,
即53sin60°=BCsin45°,
得BC=52(km).
答案:52
测量距离问题
[例1] 如图,游客从某山风景区的景点A处下山至C处有两种路径,一种是从A沿直线步行到C,另一种是先从A乘景区观光车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min 后,乙从A乘观光车到B,在B处停留20 min 后,再从B匀速步行到C.假设观光车匀速直线运行的速度为250 m/min,山路AC长为2 340 m,经测量cs A=2425,cs C=35.
(1)求观光车路线AB的长;
(2)乙出发多少分钟后,在观光车上与甲的距离最短?
解:(1)在△ABC中,因为cs A=2425,cs C=35,所以sin A=725,sin C=45,从而sin B=sin(A+C)=sin Acs C+cs Asin C=117125,由正弦定理ABsinC=ACsinB,得AB=ACsinB×sin C=2 340117125×45=2 000(m),所以观光车路线AB的长为2 000 m.
(2)假设乙出发t min后,甲、乙两游客距离为d m,则t∈[0,8],此时甲行走了(100+50t) m,乙距离A处250t m,由余弦定理得,d2=(100+50t)2+(250t)2-2×250t×(100+50t)×2425=1 000(41t2-38t+10)=1 000[41(t-1941)2+4941],因为t∈[0,8],所以当t=1941时,d取得最小值,即乙出发1941 min后,在观光车上与甲的距离最短.
距离问题的解法
选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正弦、余弦定理求解.
[针对训练] 海洋蓝洞是地球罕见的自然地理现象,被誉为“地球给人类保留宇宙秘密的最后遗产”.若要测量如图所示的海洋蓝洞的口径(即A,B两点间的距离),现取两点C,D,测得CD=80,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则图中海洋蓝洞的口径为 .
解析:由已知得,在△ADC中,∠DCA=15°,∠ADC=150°,所以∠DAC=15°,
由正弦定理得
AC=80sin150°sin15°=406-24=40(6+2).
在△BCD中,∠BDC=15°,∠BCD=135°,
所以∠DBC=30°,
由正弦定理得CDsin∠DBC=BCsin∠BDC,
得BC=CDsin∠BDCsin∠DBC=80×sin15°12=160sin 15°=40(6-2).
在△ABC中,由余弦定理,得AB2=1 600×(8+43)+1 600×(8-43)+2×1 600×(6+2)×(6-2)×12=1 600×16+1 600×4=1 600×20=32 000,
解得AB=805,
故题图中海洋蓝洞的口径为805.
答案:805
测量高度问题
[例2] (2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100;由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为(3≈1.732)( )
A.346B.373C.446D.473
解析:如图所示,根据题意过C作CE∥C′B′,交BB′于E,过B作BD∥A′B′,交AA′于D,则BE=100,
C′B′=CE=100tan15°.
在△A′C′B′中,∠C′A′B′=75°,则BD=A′B′=C'B'×sin45°sin75°.又在B点处测得A点的仰角为45°,所以AD=BD=C'B'×sin45°sin75°,所以高度差AA′-CC′=AD+BE=C'B'×sin45°sin75°+100=100tan15°×sin45°sin75°+100=100sin45°sin15°+100=
100×2222×(32-12)+100=100(3+1)+100≈373.
故选B.
(1)在测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内,视线与水平线的夹角.
(2)准确理解题意,分清已知条件与所求,画出示意图.
(3)运用正弦、余弦定理,有序地解相关的三角形,逐步求解问题的答案,注意方程思想的运用.
[针对训练] 在某运动会乒乓球男单颁奖礼上,五星红旗冉冉升起,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为96 m(如图所示),则旗杆的高度为( )
A.9 mB.27 mC.93 mD.96 m
解析:依题意可知∠AEC=45°,∠CAE=180°-60°-15°=105°,所以∠ACE=180°-45°-105°=30°,在△AEC中,由正弦定理可知AEsin∠ACE=ACsin∠AEC,所以AC=AEsin∠ACE·sin∠AEC=183(m),所以在Rt△ABC中,BC=AC·sin∠CAB=183×32=27(m).故选B.
测量角度问题
[例3] 如图,一艘海船从A出发,沿北偏东75°的方向航行60 km后到达海岛B,然后从B出发,沿北偏东15°的方向航行30 km后到达海岛C.下次若直接从A出发到达C.
(1)需要航行多少千米?
(2)此船应该沿怎样的方向航行(角度精确到0.1°)?
参考数据:sin 7.2°≈721,sin 19.1°≈2114,
sin 40.9°≈217.
解:(1)在△ABC中,∠ABC=180°-75°+15°=120°,根据余弦定理知,
AC=AB2+BC2-2AB·BCcs∠ABC
=602+302-2×60×30×cs120°
=307(km).即需要航行307 km.
(2)在△ABC中,根据正弦定理知,BCsin∠CAB=ACsin∠ABC,所以sin∠CAB=BCsin∠ABCAC=30sin120°307=2114,所以∠CAB≈19.1°,75°-∠CAB≈55.9°,即此船应该沿北偏东55.9°的方向航行.
(1)测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离,再用正弦定理或余弦定理解三角形,最后将解得的结果转化为实际问题的解.
(2)方向角是相对于某点而言的,因此在确定方向角时,必须先弄清楚是哪一个点的方向角.
[针对训练] 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡角为θ,则cs θ等于( )
A.33B.6-2
C.3-1D.2-1
解析:由题知,∠CAD=15°,∠CBD=45°,
所以∠ACB=30°,∠ABC=135°.
在△ABC中,由正弦定理得ABsin30°=ACsin135°,
又AB=100 m,所以AC=1002 m.
在△ADC中,∠ADC=90°+θ,CD=50 m,
由正弦定理得ACsin(θ+90°)=CDsin15°,
所以cs θ=sin(θ+90°)=AC·sin15°CD=3-1.故选C.
正弦、余弦定理在平面几何中的应用
[例4] 在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB=32,求BC;
(2)若AB=2BC,求cs∠BDC.
解:(1)如图所示,在△ABD中,由余弦定理可知,
cs∠ABD=
AB2+BD2-AD22AB·BD=(32) 2+12-122×32×1=34.
因为AB∥CD,所以∠BDC=∠ABD,
即cs∠BDC=cs∠ABD=34.
在△BCD中,由余弦定理可得,BC2=BD2+CD2-2BD·CDcs∠BDC=12+12-2×1×1×34=12,所以BC=22.
(2)设BC=x,则AB=2BC=2x.
在△ABD中,由余弦定理可知,
cs∠ABD=AB2+BD2-AD22AB·BD=(2x)2+12-122×2x×1=x,
在△BDC中,由余弦定理可知,cs∠BDC=CD2+BD2-BC22CD·BD=12+12-x22×1×1=2-x22.
因为AB∥CD,所以∠BDC=∠ABD,
即cs∠BDC=cs∠ABD,
可得2-x22=x,
整理得x2+2x-2=0,又x>0,
解得x=3-1.所以cs∠BDC=3-1.
平面几何中解三角形问题的求解思路
(1)把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解.
(2)寻找各个三角形之间的联系,交叉使用公共条件,求出结果.
[针对训练] 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=7,EA=2,∠ADC=2π3,且∠CBE,∠BEC,∠BCE成等差数列.
(1)求sin∠CED;
(2)求BE的长.
解:(1)在△CDE中,由余弦定理得EC2=CD2+DE2-2CD·DEcs∠EDC,
即7=CD2+1+CD,
即CD2+CD-6=0,
解得CD=2(CD=-3舍去).
由正弦定理得ECsin∠EDC=CDsin∠CED,
于是sin∠CED=CDsin 2π3EC=2×327=217.
(2)因为∠CBE,∠BEC,∠BCE成等差数列,
所以2∠BEC=∠CBE+∠BCE,
又∠CBE+∠BEC+∠BCE=π,
所以∠BEC=π3.
由题设知0<∠CED<π3,
由(1)知cs∠CED=1-sin2∠CED=1-2149=277,
又∠AEB=π-∠BEC-∠CED=2π3-∠CED,
所以cs∠AEB=cs(2π3-∠CED)=
cs 2π3cs∠CED+sin2π3sin∠CED=-12×277+32×217=714.
在Rt△EAB中,cs∠AEB=EABE=2BE=714,
所以BE=47.
[例题] 如图,高山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,测得∠ABC=120°;从B处攀登400 m到达D处,回头看索道AC,测得∠ADC=150°;从D处再攀登800 m可到达C处,则索道AC的长为 m.
解析:在△ABD中,BD=400 m,∠ABD=120°.因为∠ADC=150°,所以∠ADB=30°.
所以∠DAB=180°-120°-30°=30°.
所以AB=BD=400 m,
BC=BD+DC=1 200(m),
在△ABC中,
AC=AB2+BC2-2·AB·BC·cs120°=40013(m).
故索道AC的长为40013 m.
答案:40013
[选题明细表]
1.甲船在A处观察乙船,乙船在它的北偏东60°的方向,相距a千米的B处,乙船正向北行驶,若甲船是乙船速度的3倍,甲船为了尽快追上乙船,朝北偏东θ方向前进,则θ等于( B )
A.15°B.30°
C.45°D.60°
解析:如图,设两船在C处相遇,则由题意得∠ABC=180°-60°=120°,且ACBC=3,由正弦定理得
ACBC=sin120°sin∠BAC=3,
所以sin∠BAC=12.
又因为0°<∠BAC<60°,所以∠BAC=30°,
所以θ=30°,
所以甲船应朝北偏东30°方向前进.
2.某同学想测量某泉标的高度,于是他在广场的A点测得泉标顶部的仰角为60°,他又沿着泉标底部方向前进15.2 m,到达B点,又测得泉标顶部仰角为80°,则该同学求出泉标的高度约为(sin 20°≈0.342 0,sin 80°≈0.984 8,sin 60°≈0.866 0,结果精确到1 m)( A )
A.38 mB.50 mC.66 mD.72 m
解析:如图所示,点C,D分别为泉标的底部和顶部.
依题意,∠BAD=60°,∠CBD=80°,AB=15.2 m,
则∠ABD=100°,
故∠ADB=180°-(60°+100°)=20°.
在△ABD中,根据正弦定理,
得BDsin60°=ABsin∠ADB,
所以BD=AB·sin60°sin20°=15.2×sin60°sin20°≈38.5(m).
在Rt△BCD中,CD=BDsin 80°≈38.5×sin 80°≈38(m),即该同学求出泉标的高度约为38 m.
3.如图,一架飞机从A地飞往B地,两地相距500 km.飞行员为了避开某一区域的雷雨云层,从A点起飞以后,就沿与原来的飞行方向AB成12°角的方向飞行,飞行到中途C点,再沿与原来的飞行方向AB成18°角的方向继续飞行到终点B点.这样飞机的飞行路程比原来的路程大约多飞了(sin 12°≈0.21,sin 18°≈0.31)( B )
A.10 kmB.20 kmC.30 kmD.40 km
解析:在△ABC中,由A=12°,B=18°,
得C=150°,
由正弦定理得500sin150°=BCsin12°=ACsin18°,
所以BC=500sin150°·sin 12°≈210,
AC=500sin150°·sin 18°≈310,
所以AC+BC-AB=20(km).
4.如图,AD是某防汛抗洪大坝的坡面,大坝上有一高为20 m的监测塔BD,∠C=90°,若某科研小组在坝底A点测得∠BAD=30°,坝底到塔顶距离AB=30 m,则大坝的坡角(∠DAC)的余弦值为( D )
A.13B.223C.74D.34
解析:因为∠BAD=30°,AB=30,BD=20,在△ABD中,由正弦定理可得ABsin∠ADB=BDsin∠BAD,即30sin∠ADB=20sin30°,解得sin∠ADB=34,由∠ADB=∠C+∠DAC=90°+∠DAC,所以sin∠ADB=sin(90°+∠DAC)=cs∠DAC=34,所以大坝的坡角(∠DAC)的余弦值为34.
5.为加快推进“5G+光网”双千兆城市,如图,在东北某地地面有四个5G基站A,B,C,D,已知C,D两个基站建在松花江的南岸,距离为103 km;基站A,B在江的北岸,测得∠ACB=75°,∠ACD=120°,∠ADC=30°,∠ADB=45°,则A,B两个基站的距离为( D )
A.106 kmB.30(3-1) km
C.30(2-1) kmD.105 km
解析:在△ACD中,∠ADC=30°,∠ACD=120°,
所以∠CAD=30°,所以∠ADC=∠CAD,
所以AC=CD=103.
在△BDC中,∠BCD=120°-75°=45°,
∠CBD=180°-(75°+45°)=60°,由正弦定理得BC=103sin75°sin60°=52+56.
在△ABC中,由余弦定理得AB2=AC2+BC2-2AC·BCcs∠BCA=(103)2+(52+56)2-2×103×(52+56)cs 75°=500,所以AB=105,即两个基站A,B之间的距离为105 km.
6.(多选题)如图,△ABC的三个内角A,B,C对应的三条边分别是a,b,c,∠ABC为钝角,BD⊥BA,cs 2∠ABC=-725,c=2,b=855,则下列结论正确的是( AC )
A.sin A=55B.BD=2
C.5CD→=3DA→D.△CBD的面积为45
解析:由cs 2∠ABC=-725,
得2cs2∠ABC-1=-725,
又∠ABC为钝角,
解得cs∠ABC=-35,
在△ABC中,由余弦定理得645=a2+4-4a×(-35),解得a=2,可知△ABC为等腰三角形,即A=C,所以cs∠ABC=-cs 2A=-(1-2sin2A)=-35,解得sin A=55,故A正确;可得cs A=1-sin2A=255,在Rt△ABD中,cAD=cs A,得AD=5,可得BD=AD2-AB2=5-4=1,故B错误;CD=b-AD=855-5=355,可得|CD→||DA→|=3555=35,可得5CD→=3DA→,故C正确;S△BCD=12×2×355×55=35,故D错误.
7.(多选题)一艘轮船航行到A处时看灯塔B在A的北偏东75°,距离为126 km,灯塔C在A的北偏西30°,距离为123 km,该轮船由A沿正北方向继续航行到D处时再看灯塔B在其南偏东60°方向.下列选项正确的有( ABD )
A.AD=24
B.CD=12
C.∠CDA=60°或120°
D.∠CDA=60°
解析:如图,在△ABD中,
∠B=45°,
由ADsin45°=ABsin60°=12632=242,AD=24,A正确;在△ACD中,由余弦定理得CD2=AC2+AD2-2AC·ADcs 30°=(123)2+242-2×123×24×32=144,所以CD=12,B正确;在△ACD中,由正弦定理得CDsin30°=ACsin∠CDA,sin∠CDA=32,故∠CDA=60°或120°,因为AD>AC,故∠CDA为锐角,所以∠CDA=60°,D正确,C错误.
8.如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=223,AB=32,AD=3,则BD的长为 .
解析:因为sin∠BAC=223,且AD⊥AC,
所以sin (π2+∠BAD)=223,
所以cs∠BAD=223,在△BAD中,由余弦定理,
得BD=AB2+AD2-2AB·ADcs∠BAD=(32)2+32-2×32×3×223=3.
答案:3
9.(2021·全国乙卷)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB等于( A )
A.表高×表距表目距的差+表高B.表高×表距表目距的差-表高
C.表高×表距表目距的差+表距D.表高×表距表目距的差-表距
解析:因为FG∥AB,所以FGAB=GCCA,所以GC=FGAB·CA.因为DE∥AB,所以DEAB=EHAH,所以EH=DEAB·AH.又DE=FG,所以GC-EH=DEAB(CA-AH)=DEAB×HC=DEAB×(HG+GC)=DEAB×(EG-EH+GC).由题设中信息可得,表目距的差为GC-EH,表高为DE,表距为EG,则上式可化为,表目距的差=表高AB×(表距+表目距的差),所以AB=表高表目距的差×(表距+表目距的差)=表高×表距表目距的差+表高.
10.(多选题)如图,设△ABC内角A,B,C所对的边分别为a,b,c,3(acs∠ACB+ccs∠BAC)=2bsin B,且∠BAC=π3.若点D是△ABC外一点,DC=1,DA=3,下列说法正确的是( ABC )
A.△ABC的内角B=π3
B.△ABC的内角C=π3
C.四边形ABCD面积的最大值为532+3
D.四边形ABCD的面积无最大值
解析:因为3(acs∠ACB+ccs∠BAC)=2bsin B,
所以3(sin∠BACcs∠ACB+sin∠ACBcs∠BAC)=2sin2B,
所以3sin(∠BAC+∠ACB)=2sin2B,
所以3sin B=2sin2B,所以sin B=32,
因为∠BAC=π3,所以B∈(0,2π3),
所以B=π3,所以∠ACB=π-∠BAC-∠B=π3,因此A,B正确;四边形ABCD的面积S=S△ABC+S△ACD=34AC2+12AD·DCsin∠ADC=34(AD2+DC2-2AD·DCcs∠ADC)+12AD·DCsin∠ADC=34(9+1-6cs∠ADC)+32sin∠ADC=532+3sin(∠ADC-π3),当∠ADC=5π6时,四边形ABCD的面积有最大值为532+3,因此C正确,D错误.
11.江岸边有一炮台高30 m,江中有两条船,船与炮台底部在同一水平面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距 m.
解析:如图,由题意得OA=30 m,∠AMO=45°,∠ANO=60°,
∠MON=30°,
所以∠OAM=45°,∠NAO=30°.
OM=AO tan 45°=30(m),
ON=AOtan 30°=103(m),
在△MON中,由余弦定理得,
MN=900+300-2×30×103×32=300
=103(m).
答案:103
12.如图,已知扇形的圆心角∠AOB=2π3,半径为42,点C是AB上的一动点(不与点A,B重合).
(1)若弦BC=4(3-1),求BC的长;
(2)求四边形OACB面积的最大值.
解:(1)在△OBC中,BC=4(3-1),
OB=OC=42,
所以由余弦定理得
cs∠BOC=OB2+OC2-BC22OB·OC=32,
所以∠BOC=π6,
于是BC的长为π6×42=22π3.
(2)设∠AOC=θ,θ∈(0,2π3),
则∠BOC=2π3-θ,S四边形OACB=S△AOC+S△BOC
=12×42×42sin θ+12×42×42·sin(2π3-θ)
=24sin θ+83cs θ=163sin(θ+π6).
由于θ∈(0,2π3),所以θ+π6∈(π6,5π6),
故当θ=π3时,四边形OACB的面积取得最大值163.
13.如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:km).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远)?
解:设∠AMN=θ,在△AMN中,
MNsin60°=AMsin(120°-θ).
因为MN=2,所以AM=433sin(120°-θ).
在△APM中,cs∠AMP=cs(60°+θ).
AP2=AM2+MP2-2AM·MP·cs∠AMP=
163sin2(120°-θ)+4-2×2×433sin(120°-θ)·cs(60°+θ)=163sin2(θ+60°)-1633sin(θ+60°)·cs(θ+60°)+4=83[1-cs(2θ+120°)]-
833sin(2θ+120°)+4=-83[3sin(2θ+120°)+cs(2θ+120°)]+203=203-163sin(2θ+150°),0°<θ<120°.当且仅当2θ+150°=270°,
即θ=60°时,AP2取得最大值12,
即AP取得最大值23.所以设计∠AMN=60°时,工厂产生的噪声对居民的影响最小.
术语
名称
术语意义
图形表示
仰角与
俯角
在目标视线与水平视线(两者在同一铅垂平面内)所成的角中,目标视线在水平视线上方的叫做仰角,目标视线在水平视线下方的叫做俯角
方位角
从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角.方位角θ的范围是0°≤θ<360°
方向角
正北或正南方向线与目标方向线所成的锐角,通常表达为北(南)偏东(西)α
例:(1)北偏东α:
(2)南偏西α:
坡角与
坡比
坡面与水平面所成的锐二面角叫坡角(θ为坡角);坡面的垂直高度与水平长度之比叫坡比(坡度),即i=ℎl=tan θ
知识点、方法
题号
测量距离问题
3,5,11
测量高度问题
2,9
测量角度问题
1,4
正弦、余弦定理在平面几何中的应用
6,8,10
综合问题
7,12,13