2024年山东省泰安市东平县中考二模数学试题（原卷版+解析版）

这是一份2024年山东省泰安市东平县中考二模数学试题（原卷版+解析版），文件包含2024年山东省泰安市东平县中考二模数学试题原卷版docx、2024年山东省泰安市东平县中考二模数学试题解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。

1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中选择题48分，非选择题102分，满分150分，考试时间120分钟；
2．选择题选出答案后，用2B铅笔把答题卡上对应题目的正确答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案，答案写在试卷上无效；
3．数学考试不允许使用计算器，考试结束后，应将答题卡交回．
第Ⅰ卷（选择题 共48分）
一、单选题（本大题共12个小题，每小题4分，共48分．每小题给出的四个答案中，只有一项是正确的．）
1. 下列等式正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了平方根、算术平方根和立方根的定义，解题的关键是掌握所学的知识进行判断．
根据平方根、算术平方根和立方根的运算法则即可求出答案．
【详解】解：A、，故A错误．
B、，故B错误．
C、，故C错误．
D、，故D正确．
故选：D．
2. 下列运算正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题主要考查了同底数幂乘除法计算，积的乘方计算和完全平方公式，熟知相关计算法则是解题的关键．
【详解】解：A、，原式计算正确，符合题意；
B、，原式计算错误，不符合题意；
C、，原式计算错误，不符合题意；
D、，原式计算错误，不符合题意；
故选：A．
3. 据中科院国家天文台，基于我国郭守敬望远镜和美国APOGEE巡天的观测数据，我国天文学家精确测量了距离银河系中心1.6万光年至8.1万光年范围内的恒星运动速度，并估算出银河系的“体重”约为8050亿个太阳质量，其中数据“8050亿”用科学记数法可表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查科学记数法，根据科学记数法的表示方法：为整数，进行表示即可．
【详解】解：8050亿；
故选C．
4. 在下列四项竞技运动的图案中，是中心对称图形的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了中心对称图形的识别．熟练掌握如果把一个图形绕某一点旋转后能与自身重合，这个图形是中心对称图形是解题的关键．
根据中心对称图形定义进行判断即可．
【详解】解：A中不是中心对称图形，故不符合要求；
B中是中心对称图形，故符合要求；
C中不是中心对称图形，故不符合要求；
D中不是中心对称图形，故不符合要求；
故选：B．
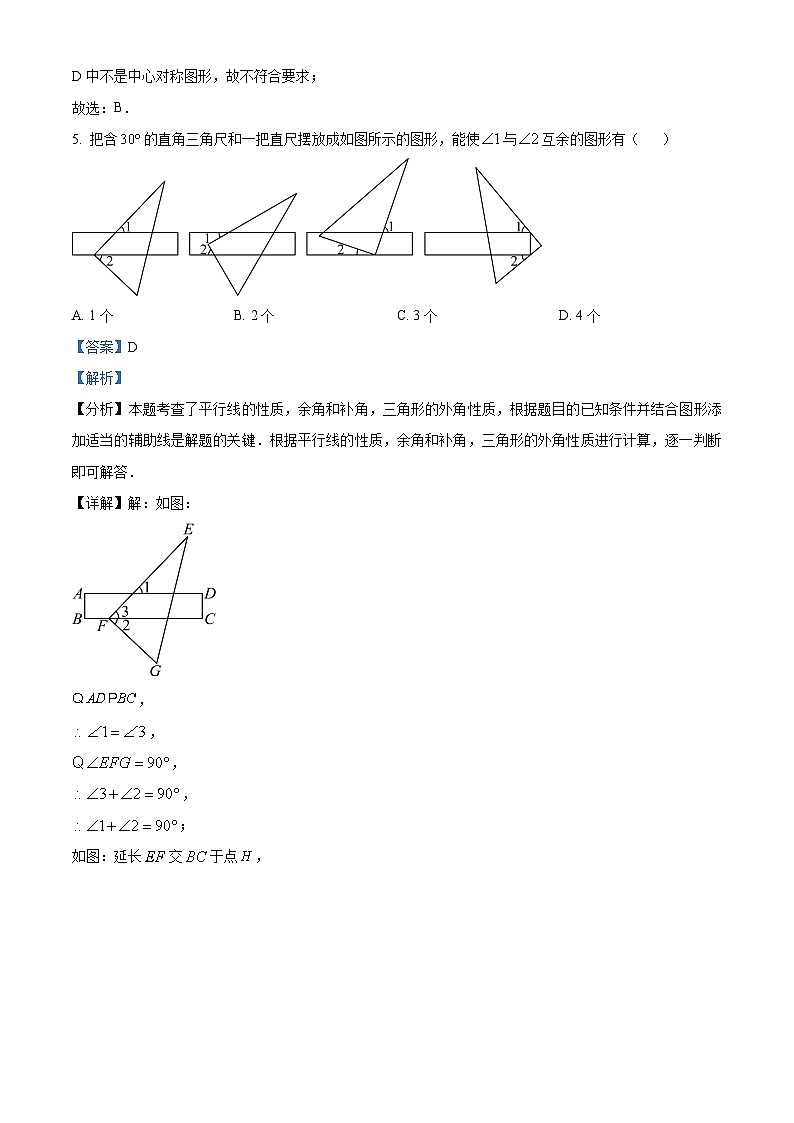
5. 把含的直角三角尺和一把直尺摆放成如图所示的图形，能使与互余的图形有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
【分析】本题考查了平行线的性质，余角和补角，三角形的外角性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．根据平行线的性质，余角和补角，三角形的外角性质进行计算，逐一判断即可解答．
【详解】解：如图：
，
，
，
，
；
如图：延长交于点，
，
，
是的一个外角，
，
；
如图：
，
，
，
，
；
如图：过点作，
，
，
，
，
，
，
；
所以，能使与互余的图形有4个，
故选：D
6. 在元旦节目汇演比赛中，7位评委给某节目打分，得到互不相等的7个分值，同时去掉一个最高分和一个最低分，则以下四种统计量中一定不会发生改变的是（ ）
A. 平均数B. 中位数C. 方差D. 标准差
【答案】B
【解析】
【分析】本题考查了平均数、中位数、众数、方差，根据平均数、众数、中位数、方差的意义即可求解．
【详解】解：根据题意，从7个原始评分中去掉个最高分和个最低分，得到5个有效评分．
5个有效评分与7个原始评分相比，不变的是中位数．
故选：B．
7. 如图，已知的两条弦相交于点，那么的值为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】此题重点考查学生对圆内角的大小的理解，对顶角相等是解本题的关键根据已知角和对顶角相等，可以求出的大小，进而得出的值
【详解】已知的两条弦，相交于点，,
,
∵
故选：
8. 如图是抛物线（a，b，c是常数且）的图象，则双曲线和直线的大致图象可能是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查了二次函数的图象和性质，一次函数以及反比例函数的图象与系数的关系；
根据，可得，则双曲线的图象位于一、三象限；根据抛物线的图象判断出，，，可得，然后根据一次函数的图象与系数的关系进行判断．
【详解】解：根据抛物线的图象可得，当时，，即，
∴双曲线的图象位于一、三象限；
∵抛物线的开口向上，
∴，
∵抛物线的对称轴位于y轴左侧，
∴，
∴；
∵抛物线与y轴交于原点下方，
∴，
∴，
∴直线经过第一、二、四象限，
综上，选项A符合题意，
故选：A．
9. 如图，将扇形沿方向平移，使点平移到的中点处，得到扇形．若，，则阴影部分的面积为（ ）
A. 6B. C. D.
【答案】B
【解析】
【分析】如图，设与交于点，连接，则，由，可得，则，可得， ，，由平移的性质，得，根据，计算求解即可．
详解】解：如图，设与交于点，连接，

点是的中点，，
∴，
∵，
∴，
由平移的性质，得，即，
∵，
∴，
∴ ，，
由平移的性质，得，
∴，
故选：B．
【点睛】本题考查了平移的性质，余弦，正切，扇形面积．正确表示阴影部分面积是解题的关键．
10. 我国明代《算法统宗》一书中有如下的类似问题：“一支竿子一条索，索比竿子长两托，对折索子来量竿，却比竿子短一托（一托按照5尺计算）．”大意是：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长10尺；如果将绳索对折后再去量竿，就比竿短5尺．如果此题中设竿长x尺，绳索长y尺，根据题意可列方程组为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了二元一次方程组，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．本题要注意前后两次绳和杆的数量关系．设竿长x尺，绳索长y尺，根据第一次用绳索去量竿，绳索比竿长10尺，第二次将绳索对折去量竿，就比竿短5尺，则可得方程组．
【详解】解：设竿长x尺，绳索长y尺，
由题意可得：，
故选：B．
11. 如图，在中，，．按照如下步骤作图：
①分别以点为圆心，大于的长为半径作弧，两弧相交于点；
②作直线，交点；
③以为圆心，长为半径作弧，交的延长线于点；
④连接．
下列说法错误的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据等腰三角形的性质以及三角形内角和定理可得，再根据题意可得：，是的垂直平分线，从而可得，进而可得，然后利用角的和差关系可得，从而利用三角形的外角性质可得，进而可得，再根据等量代换可得，从而可得，进而可得，即可判断A、B，然后证明，从而利用相似三角形的性质可得，即可判断C，根据等腰三角形的性质相似三角形的性质，可得即可判断D．
【详解】解：，，
，
由题意得：，是的垂直平分线，
，
，
，
，
，
，
，故A正确；
，
，
，
，故B正确；
，，
，
，
，故C正确；
设，则，
解得：(负值舍去)
又∵
∴，故D选项错误，
故选：D．
【点睛】本题考查了相似三角形的性质与判定，等腰的性质，作垂直平分线，线段垂直平分线的性质，等腰三角形的性质，熟练掌握相似三角形的判定与性质是解题的关键．
12. 如图，矩形，，，点是边上的动点，点F是射线BC上的动点，且，连接，．若，则m的最小值为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】延长到G，使，连接、，得到，从而可得，再利用勾股定理即可求出最小值．
【详解】解：如图，延长到G，使，连接、，

在矩形，，
∴，
又∵，
∴，
∴
∴，即，
∵，
∴，
∴当G、E、C三点共线时，m取最小值为GC，
，
∴m的最小值为．
故选C．
【点睛】本题主要考查了矩形的性质、相似三角形的判定和性质、最短距离问题，一般求两条线段最短距离问题，都转化为一条线段．本题通过构造，得到，利用两点间线段最短解决m取最小值的问题．
第Ⅱ卷（非选择题 共102分）
二、填空题（本大题共6个小题，每小题4分，共24分，只要求填写最后结果）
13. 已知关于x方程有至少一个实数解，则a的取值范围是_______．
【答案】
【解析】
【分析】本题考查根据方程的解的情况求字母系数取值范围．熟练掌握一元二次方程有解，则是银题的关键．注意分类讨论．
分两种情况讨论：当时，方程为一元一次方程，有一个实数解；当时，方程是一元二次方程，则当时，方程有实数解，求解即可．
【详解】解：当时，原方程为：，则方程为一元一次方程，有一个实数解；
当时，方程是一元二次方程，则当时，方程有实数解，
解得：，
综上，关于x的方程有至少一个实数解，则a的取值范围是．
故答案为：．
14. 如图，在中，，，，O为边上的一点，以为半径的半圆O交于点D、交AC于点E，过点D作半圆O的切线交边于点F，且，则的半径为__________．

【答案】
【解析】
【分析】本题考查切线性质，等边三角形的判定和性质，勾股定理，连接，易得，为等边三角形，设圆的半径为，由勾股定理可得：，列出方程进行求解即可．
【详解】解：∵，，，
∴，
∴，
连接，则：，

∴，
∵是切线，
∴，
∴，
∴，
∴，
∴为等边三角形，
∴，
设的半径为，则：，
由勾股定理，得：，
∴，
解得：；
故答案为：．
15. 在平面直角坐标系中，抛物线的图象如图所示，对任意的，称W为a到b时y的值的“极差”（即时y的最大值与最小值的差），L为a到b时x的值的“极宽”（即b与a的差值），则当时，W的取值范围是___________．

【答案】
【解析】
【分析】本题主要考查了二次函数的最值，解题时要熟练掌握并能灵活运用是关键．
依据题意，由，从而可得抛物线的对称轴是直线，顶点坐标为，再由，从而，结合题意可得，结合二次函数的性质可得，当时，有最大值，最大值为；当时，有最小值，最小值为，故，进而可得的范围．
【详解】解：根据题意可得：，
抛物线的对称轴是直线，顶点坐标为．
，即与的差值为7，
．
，即，
．
．
当时，随增大而增大，当时，随的增大而减小，
当时，有最大值，最大值为．
当时，有最小值，最小值为，
．
对称轴是直线．
当时，随的增大而增大．
当时，有最小值，最小值为4．
当时，有最大值，最大值为．
综上所述：．
故答案为：
16. 图①是某款电动平衡车，图②是其简化示意图，该款平衡车的座位AB和底盘CD均平行于地面，座位AB可沿射线EF方向调节，当座位AB的位置最低时，支架，，支架EF与座位AB的夹角，与支架GE的夹角，底盘CD到地面的距离为，则此时座位AB到地面的高度为___．（结果精确到1cm，参考数据：，，）
【答案】60
【解析】
【分析】本题考查了解直角三角形的应用．过点E作，垂足为H，延长交的延长线于点M，根据已知易得：，然后在中，利用锐角三角函数的定义可求出的长，再在中，利用锐角三角函数的定义可求出的长，最后利用线段的和差关系进行计算，即可解答．
【详解】解：过点E作，垂足为H，延长交的延长线于点M，
∵，
∴，
在中，，，
∴，，
∵，
∴，
在中，，
∴，
∵底盘到地面的距离为，
∴此时座位到地面的高度，
故答案为：60．
17. 南宋数学家杨辉在其著作《详解九章算法》中揭示了（为非负整数）展开式的项数及各项系数的有关规律，后人也将下表称为“杨恽三角”．则：中，第三项系数为_____．






【答案】
【解析】
【分析】此题考查了数字的变化规律，根据题意得到第三项系数的规律即可解答，能够根据所给杨辉三角，观察得出系数的变化规律是解题的关键．
【详解】解：由题意可得，的第三项系数为，
的第三项系数为，
的第三项系数为，
的第三项系数为，
，
的第三项系数为，
故答案为：．
18. 已知等腰中，，，点D是边的中点，沿翻折，使点A落在同一平面的点E处，若，则______．
【答案】
【解析】
【分析】本题考查了翻折的性质，相似三角形的判定与性质，勾股定理等知识．熟练掌握翻折的性质，相似三角形的判定与性质，勾股定理是解题的关键．
记的交点为F，设，，则，，，由翻折的性质可知，，，，证明，则，即，可得，则，由勾股定理得，，即，整理得，；，即，整理得，；得，，可求，则，，由勾股定理得，，即，可求满足要求的解，，进而可求的值．
【详解】解：如图，记的交点为F，设，，则，，，
由翻折的性质可知，，，，
∵，
∴，，
∵，，
∴，
∴，即，
解得，，
∴，
由勾股定理得，，即，整理得，；
，即，整理得，；
得，，
∴，
∴，，
由勾股定理得，，即，
解得，或（舍去），
∴，
故答案为：．
三、解答题（本大题共7个小题，共78分，写出必要的文字说明、证明过程或推演步骤．）
19. （1）计算
（2），其中．
【答案】（1）1；（2）；5
【解析】
【分析】本题主要考查了实数混合运算，分式化简求值，解题的关键是熟练掌握运算法则，准确计算．
（1）根据特殊角三角函数值，零指数幂和负整数指数幂运算法则，算术平方根定义，进行计算即可；
（2）先根据分式混合运算法则进行化简，然后代入数据进行计算即可．
【详解】解：（1）
；
（2）
，
当时，原式．
20. 非物质文化遗产是中华民族古老生命记忆和活态的文化基因．某学校为了让学生深入了解非物质文化遗产，决定邀请舞狮，农民画，剪纸，传统武术，凉帽（竹编技艺）的相关传承人进校园宣讲，现随机抽取若干名七年级学生进行投票，选择自己喜欢的项目（假设每名学生只能选择一项），并将投票结果绘制成如下两幅不完整的统计图：

根据以上信息，解决下列问题：
（1）参与此次抽样调查的学生共__________人，补全统计图（要求在条形图上方注明人数）；
（2）若七年级学生共有人，根据调查结果，试估计七年级喜欢“传统武术”项目的学生人数；
（3）若该学校决定邀请两个项目的非遗传承人进校园宣讲，请用画树状图或列表的方法，求选中农民画和剪纸这两个项目的概率．
【答案】（1），见解析；
（2）人；
（3）．
【解析】
【分析】（）从两个统计图中可得样本中投票“”的有人，占调查人数的，根据即可求出答案，进而补全条形统计图；
（）求出样本中投票“”所占的百分比，求出相应人数即可；
（）用列表法表示所有可能出现的结果，进而求出相应的概率即可；
本题考查了扇形统计图、条形统计图，列表法或树状图法求简单随机事件的概率，理解条形统计图、扇形统计图中数量之间的关系以及列举出所有可能出现的结果是解题的关键．
【小问1详解】
调查学生总数为（人），
补全统计图如下：

故答案为：；
【小问2详解】
（人），
答：七年级喜欢“传统武术”项目的学生人数有人；
【小问3详解】
列表如下：
共有种可能出现的结果，其中恰好选中，这两个项目的有种，
所以恰好选中，这两个项目的概率为．
21. 如图，在平面直角坐标系中，一次函数的图象与y轴交于点A，与反比例函数交于点B．
（1）求点A和点B的坐标；
（2）点C是x轴正半轴上一点，连接交反比例函数于点D，连接，若，求的面积；
（3）在（2）的条件下，将线段绕点D顺时针旋转得到线段，求点E的坐标．
【答案】（1），；
（2）；
（3）
【解析】
【分析】此题考查了反比例函数和一次函数的交点问题，相似三角形的判定和性质、全等三角形的判定和性质，数形结合是解题的关键．
（1）求出点A的坐标，联立一次函数和反比例函数求出答案即可；
（2）过点B作轴于点G，过点D作轴于点H，设交y轴于点K，证明，则，得到，求出点，由求出，得到，求出直线的解析式为，得到，则，利用即可求出答案；
（3）过点D作轴，作于H，于G，连接，证明，则，，即可得到．
【小问1详解】
解：在中，当时，，
，
联立方程组，
解得：，（舍去），
；
【小问2详解】
解：如图，过点B作轴于点G，过点D作轴于点H，设交y轴于点K，
，
，
，
，
，
当时，，
解得：，
，
，
，
，
，
，
，
设直线BC的解析式为，
则，
解得：，
直线BC的解析式为，
当时，，
，
，
；
【小问3详解】
过点D作轴，作于H，于G，连接，如图，
由旋转得：，，
，
，
，
，，
∵，
∴点E的坐标为
．
22. 某粮食生产基地计划投入一笔资金购买甲、乙两种农机具，已知1件甲种农机具比1件乙种农机具多2万元，用30万元购买甲种农机具的数量和用20万元购买乙种农机具的数量相同．
（1）求购买1件甲种农机具和1件乙种农机具各需多少万元？
（2）若该粮食生产基地计划购买甲、乙两种农机具共20件，且购买的总费用不超过92万元，乙的数量不超过甲数量的4倍，则如何购买费用最低？最低费用是多少万元？
【答案】（1）购买1件甲种农机具需6万元，1件乙种农机具需4万元
（2）购买甲4件，乙16件最优惠，费用为88万元
【解析】
【分析】本题考查了分式方程的应用以及一元一次不等式的应用．
（1）设购买1件乙种农机具需x万元，则购买1件甲种农机具需万元，利用数量=总价÷单价，结合用30万元购买甲种农机具的数量和用20万元购买乙种农机具的数量相同，即可得出关于x的分式方程，解之经检验后即可；
（2）设该粮食生产基地计划购买甲种农机具m件，则计划购买乙种农机具件，利用总价=单价×数量，结合购买的总费用不超过92万元，乙的数量不超过甲数量的4倍，即可得出关于m的一元一次不等式组，解之取其中的最值即可得出结论．
【小问1详解】
设购买1件乙种农机具需x万元，则购买1件甲种农机具需万元，
根据题意得，
解得，
经检验，是原方程的解，
∴，
答：购买1件甲种农机具需6万元，1件乙种农机具需4万元．
【小问2详解】
设该粮食生产基地计划购买甲种农机具m件，则计划购买乙种农机具件，
根据题意得，，
解得，
所以共有三种方案，
当时，购买甲4件，乙16件，费用（万元）；
当时，购买甲5件，乙15件，费用（万元）；
当时，购买甲6件，乙14件，费用（万元）；
∴购买甲4件，乙16件总费用费用最低，最低费用：（万元）
答：购买甲4件，乙16件最优惠，费用为88万元．
23. 已知矩形中，是的中点，于点．
（1）如图1，若，求的值；
（2）如图2，连接交于点，若，求的值．
【答案】（1）
（2）
【解析】
【分析】本题考查矩形的性质，相似三角形的判定与性质，菱形的判定与性质，含角的直角三角形的性质．
（1）证明，得即即可；
（2）延长交的延长线于，连接，先证明得，故得，再证明四边形是菱形，得，，，故得，最后求即可．
【小问1详解】
解：是的中点，
，
四边形是矩形，
，，
，
，
，
，
，
；
【小问2详解】
延长交的延长线于，连接，如图2所示：
四边形是矩形，
，，，
，
，
，
是的中点，
，
，
四边形是平行四边形，
，
四边形是菱形，
，，，
，
，
，
，
，
，
，
，
．
24. 如图1，在平面直角坐标系中，抛物线与轴相交于点，点在轴上，且，过点作轴的垂线交抛物线于点，当时，．
（1）求抛物线的解析式；
（2）如图2，作直线交轴于点，若，求的值；
（3）如图3，点是线段上的点，且，过点作轴的垂线交于点，交抛物线于点，是否存在合适的值，使四边形是平行四边形？若存在，请求出的值；若不存在，请说明理由．
【答案】（1）
（2）
（3）存在，
【解析】
【分析】（1）先求得，再用待定系数法求解即可；
（2）先用待定系数法求出直线解析式，再把代入求解即可；
（3）求出，，，，则，，根据，得，求解即可．
【小问1详解】
解：∵，，轴，
∴
把，代入，得
解得：，
∴．
【小问2详解】
解：∵点C在抛物线上，
∴，
设直线解析式为，
把，代入，得
，
解得：，
∴直线解析式为，
∵，，
∴
∴
把代入，得
解得：．
∵
∴
【小问3详解】
解：∵，，
∴，
对于抛物线，当时，，
∴，
由（2）知：直线解析式为，
当时，
∴
∴
∵
∴，，
∴，
∵轴，轴，
∴当时，四边形是平行四边形，
∴
解得：，
∵
∴
∴存在，当时，四边形是平行四边形．
【点睛】本题考查二次函数与特征四边形综合，待定系数法求二次函数解析式，待定系数法求一次函数解析式，平行四边形的判定，二次函数与一次函数图象上点的坐标特征，解一次二次方程．熟练掌握用待定系数法求函数解析式和平行四边形的判定是解题的关键．
25. 如图，为的直径，是圆上一点，是的中点，于点，延长至点，连接，，
（1）求证：是的切线；
（2）若点是上的一点，连接、，，．
①求的值；
②若为的角平分线，求的长．
【答案】（1）见详解 （2）①；②
【解析】
【分析】（1）根据，证明，再根据圆周角定理得出，即可证明，即可证明；
（2）①连接，证明，设的半径为，利用相似三角形的性质得，由勾股定理求得，得到，即可得到；
②过点作交于点，证明是等腰直角三角形，解直角三角形得到，由得到，解得，由即可求解．
【小问1详解】
连接，
∵，
∴，
∵，
∴，
∴，
∵为的直径，
∴，
∴，
∴是的切线；
【小问2详解】
①解：连接，
∵是的中点，
∴，
∴，
∵为的直径，
∴，
∵，
∴，
∴，
∴，
设的半径为，则，
解得，
经检验，是方程的解，
，
，
，
，
；
②如图，过点作交于点，
，
是的角平分线，
，
，
，
，
，
，
．
【点睛】本题考查了相似三角形的判定与性质，垂径定理，圆周角定理及推论，解直角三角形等知识，熟练掌握以上知识并灵活运用是解题的关键．