2024年江苏省盐城市两校联考中考二模数学试题

这是一份2024年江苏省盐城市两校联考中考二模数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．2024的倒数是（ ）
A．2024B．C．D．
2．2024年7月26日至8月11日第33届奥运会将在法国巴黎举行，下列是与奥运会有关部分图案，其中是中心对称图形的是（ ）
A．B．C．D．
3．下列运算正确的是（ ）
A．B．C．D．
4．若代数式的值为1，则代数式的值为（ ）
A．5B．C．4D．
5．如图①是由5个大小相同的小正方体组成的几何体，移走一个小正方体后，余下几何体的主视图如图②所示，则移走的小正方体是（ ）
A．①B．②C．③D．④
6．如果两个相似三角形的周长比为，那么这两个相似三角形的面积比为（ ）
A．B．C．D．
7．一技术人员用刻度尺（单位：）测量某三角形部件的尺寸．如图所示，已知，点为边的中点，点对应的刻度分别为1、7，则的长度为（ ）
A．B．C．D．
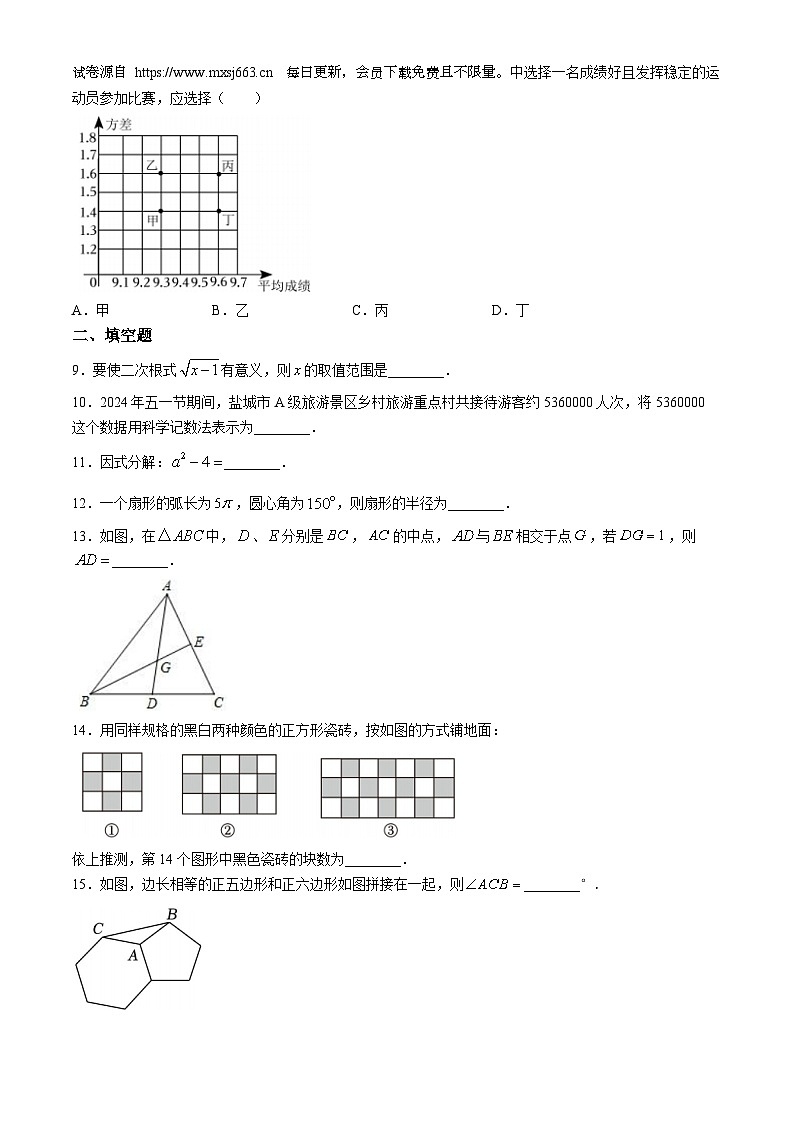
8．甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差如图所示，根据图中数据，要从试卷源自 每日更新，会员下载免费且不限量。中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（ ）
A．甲B．乙C．丙D．丁
二、填空题
9．要使二次根式有意义，则的取值范围是________．
10．2024年五一节期间，盐城市A级旅游景区乡村旅游重点村共接待游客约5360000人次，将5360000这个数据用科学记数法表示为________．
11．因式分解：________．
12．一个扇形的弧长为，圆心角为，则扇形的半径为________．
13．如图，在中，、分别是，的中点，与相交于点，若，则________．
14．用同样规格的黑白两种颜色的正方形瓷砖，按如图的方式铺地面：
依上推测，第14个图形中黑色瓷砖的块数为________．
15．如图，边长相等的正五边形和正六边形如图拼接在一起，则________°．
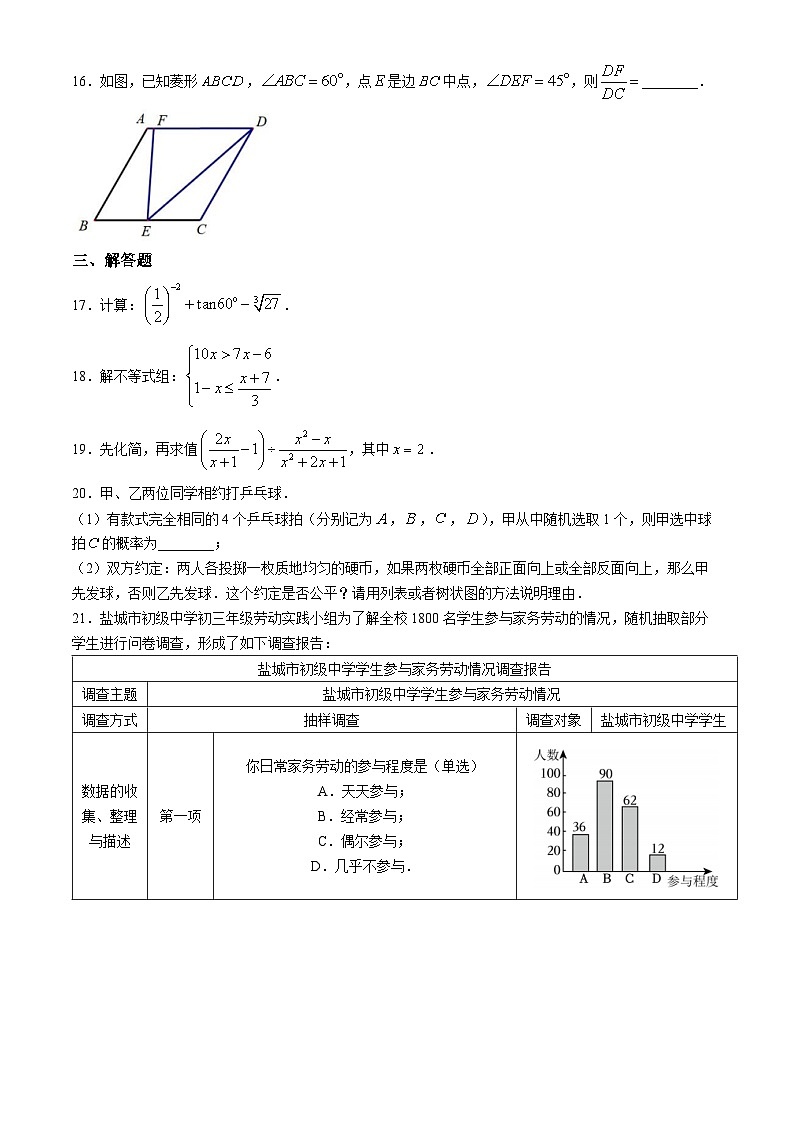
16．如图，已知菱形，，点是边中点，，则________．
三、解答题
17．计算：．
18．解不等式组：．
19．先化简，再求值，其中．
20．甲、乙两位同学相约打乒乓球．
（1）有款式完全相同的4个乒乓球拍（分别记为，，，），甲从中随机选取1个，则甲选中球拍的概率为________；
（2）双方约定：两人各投掷一枚质地均匀的硬币，如果两枚硬币全部正面向上或全部反面向上，那么甲先发球，否则乙先发球．这个约定是否公平？请用列表或者树状图的方法说明理由．
21．盐城市初级中学初三年级劳动实践小组为了解全校1800名学生参与家务劳动的情况，随机抽取部分学生进行问卷调查，形成了如下调查报告：
请根据以上调查报告，解答下列问题：
（1）参与本次抽样调查的学生有________人；
（2）若将上述报告第一项的条形统计图转化为相对应的扇形统计图，则扇形统计图中选项“天天参与”对应扇形的圆心角度数为________°；
（3）估计该校1800名学生中，参与家务劳动项目为“整理房间”的人数为________；
（4）作为我校的学生，为鼓励同学们更加积极地参与家务劳动，请你面向全体同学写出一条倡议．
22．如图，在平行四边形中，、分别是、边上的点，且．
（1）求证：四边形是平行四边形；
（2）连接，若平分，，，求平行四边形的周长．
23．为增强民众生活幸福感，某社区服务队在休闲活动场所的墙上安装遮阳棚，方便居民使用．如图，在侧截面示意图中，遮阳棚长4米，与水平线的夹角为，且靠墙端离地的高为5米，当太阳光线与地面的夹角为时，求的长．（结果精确到0.1米；参考数据：，，，）
24．如图，点是的边上的一定点．
（1）如图1，直线是线段的垂直平分线且交射线于点，求证：．
（2）在图2中，请用无刻度的直尺和圆规，在射线上作点，使得．（保留作图痕迹，不写作法）
25．如图，点、分别在反比例函数、在第一象限的图象上，轴，且．
（1）若点的坐标为，求的值．
（2）若点、分别在反比例函数、在第一象限的图象上，如图2，，且，与之间的距离为2，连接、，求的面积．
26．综合与实践
折纸中蕴藏着丰富的数学知识，也启迪着数学问题的解决．综合实践课上，老师和同学们一起通过折纸，探究数学的奥秘．
【折纸探究】
如图1，在矩形纸片中，点、分别在边和上，将矩形纸片沿折叠，点落在边上的点处，点落在点处，连接，则与的位置关系为________；
折叠一：小明发现，当点和点重合时，连接，如图2，则有，请说明理由；
折叠二：如图3，若矩形是一张A4纸，探究、和三者之间的数量关系，并说明理由；
【解决问题】
小华受【折纸探究】的启发，解决了下面的问题．
如图4，在矩形纸片中，点、分别在边和上，连接、、，平分，，，求的值．（用含有的代数式表示）
27．定义：当（，为常数，）时，函数最大值与最小值之差恰好为，我们称函数是在上的“雅正函数”，“”的值叫做该“雅正函数”的“雅正值”．
【初步理解】
（1）试判断下列函数是在上的“雅正函数”为________．（填序号）
①；②；③．
【尝试应用】
（2）若一次函数（，为常数，）和反比例函数（为常数，）都是在上的“雅正函数”，求的值．
【拓展延伸】
（3）若二次函数是在（，为常数，）上的“雅正函数”，雅正值是3．
①求、的值；
②若该二次函数图象与轴交于点，（点在点的左侧），与轴交于点．点为二次函数图象上一点，且点的横坐标为，点、点是线段上的两个动点（点在点的左侧），分别过点、点作轴的平行线交抛物线于点、点，如果，其中为常数．试探究：是否存在常数，使得为定值．如果存在，请求出的值；如果不存在，请说明理由．
【参考公式：】
初三年级第二次模拟考试数学试卷（答案）
一、选择题（本题共24分，每小题3分）
二、填空题（本题共24分，每题3分）
9．；10．；11．；12．6；
13．3；14．43；15．24；16．．
三、解答题
17．（6分）原式4分
2分
18．（6分）解不等式①得，2分
解不等式②得，4分
∴不等式组的解集为6分
19．（8分）原式5分
将代入得，
原式．8分
20．（8分）
（1）3分
（2）画树状图如下：
第2枚
6分
一共有4种等可能的结果，其中两枚硬币全部正面向上或全部反面向上有2种可能的结果，
∴（甲先发球），
（乙先发球），
∵（甲先发球）（乙先发球），
∴这个约定公平．8分
21．（8分）
（1）2002分
（2）4分
（3）14946分
（4）同学们可在家多帮助父母扫地抹桌和洗晒衣服（合理即可）．8分
22．（10分）
（1）∵四边形是平行四边形，
∴，，
∵，
∴，1分
∴，
∵，
∴四边形是平行四边形；4分
（2）∵四边形是平行四边形，
∴，，，
∴，
∵平分，
∴，
∴，
∴，
∴，
∴，
∴平行四边形的周长．10分
23．（10分）
过点作交于点，过点作交于点，
在中，，，
∴，
∴，
∵，
∴，4分
∴，
∴，6分
在中，，，
∴，
∴，8分
∴10分
24．（10分）
（1）∵直线是线段的垂直平分线且交射线于点，
∴，2分
∴，
∵是的外角，3分
∴，5分
（2）10分
25．（10分）
（1）∵点的坐标为，轴，，
∴，
∵点在反比例函数的图象上，点在反比例函数的图象上，
∴，，
∴．4分
（2）设点的纵坐标为，则点的纵坐标为，
∵轴，，
∴，，
∴，
∴，
∵，，
∴，，
∴，
∴，
∴，
∴，
∴．
∴．10分
26．（12分）【折纸探究】
2分
折叠一：连，交于点．
∵点和点关于对称
∴，
∴
∵四边形是矩形
∴
∴
∵
∴
∴．5分
折叠二：过点作，垂足为，连接，交于点，连接．
∵，∴
∵四边形是矩形
∴
∴四边形是矩形
∴
∵点和点关于对称
∴，
∴
∵，
∴
∴
∵，
∴，
∴
∴，即：．8分
【解决问题】
延长到点，使得，连接，交于点，连接．
∵平分
∴
∴
转化为“折叠二”问题，
∴，
∵
∴
∵
∴
∴．12分
27．（14分）
（1）②③3分
（2），4分
，5分
7分
（3）①，10分
②由题意可知，，，，，∴，
∵
∴
∵为常数
∴为常数
∴
∴14分
盐城市初级中学学生参与家务劳动情况调查报告
调查主题
盐城市初级中学学生参与家务劳动情况
调查方式
抽样调查
调查对象
盐城市初级中学学生
数据的收集、整理与描述
第一项
你日常家务劳动的参与程度是（单选）
A．天天参与；
B．经常参与；
C．偶尔参与；
D．几乎不参与．
第二项
你日常参与的家务劳动项目是（可多选）
E．扫地抹桌；
F．厨房帮厨；
G．整理房间；
H．洗晒衣服．
第三项
…
…
调查结论
…
题号
1
2
3
4
5
6
7
8
答案
C
C
B
A
D
A
A
D