人教版七年级数学上册专题06整式中规律探索的三种考法(原卷版+解析)

这是一份人教版七年级数学上册专题06整式中规律探索的三种考法(原卷版+解析)，共18页。试卷主要包含了单项式规律性问题，数字类规律探索，图形类规律探索等内容，欢迎下载使用。

例．有一列式子，按一定规律排列成，，，，，…，第n个式子为 （n为正整数）．
【变式训练1】观察下列单项式：按此规律，可以得到第2020个单项式是 ．
【变式训练2】有一组单项式依次为根据它们的规律，第个单项式为 ．
类型二、数字类规律探索
例．如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点．若青蛙从数1这点开始跳，第1次跳到数3那个点，如此，则经2015次跳后它停的点所对应的数为 （ ）
A．5B．3C．2D．1
【变式训练1】按上面数表的规律．得下面的三角形数表：
（1）上表中，第九行有 个算式，第九行最中间的算式是 ．
（2）把下表中的数从小到大排成一列数：3，5，6，9，10，12，…则第15个数是 ，
【变式训练2】将正整数按如图所示的规律排列，有序数对表示第排，从左到右第个数．如有序数对表示8，则有序数对表示的数为 ．
【变式训练3】斐波那契数列因意大利数学家斐波那契以兔子繁殖为例引入，故又称为“兔子数列”，即：1，1，2，3，5，8，13，21，34，…实际生活中及现代物理与化学等领域也有着广泛的应用，若斐波那契数列中的第n个数记为，则与斐波那契数列中的第 个数相同．
【变式训练4】观察下列一组数：2，，，…，它们按一定规律排列，第n个数记为，且满足．则 ， ．
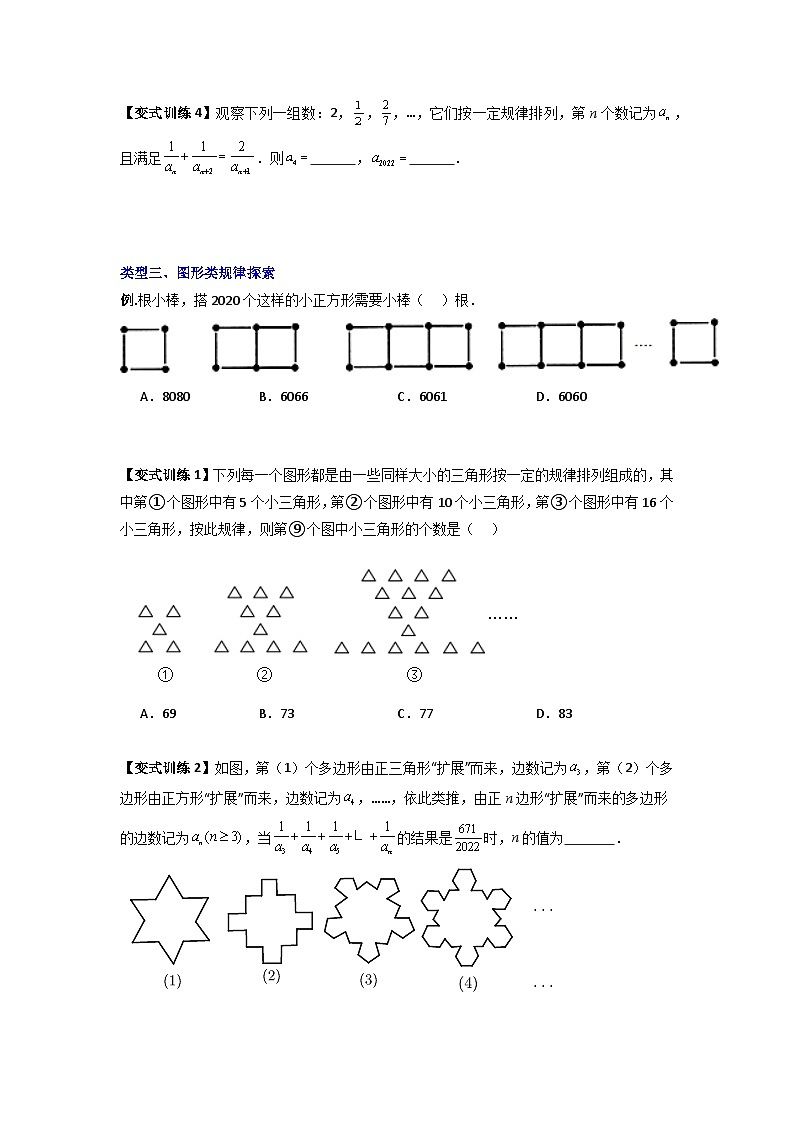
类型三、图形类规律探索
例.根小棒，搭2020个这样的小正方形需要小棒（ ）根．
A．8080B．6066C．6061D．6060
【变式训练1】下列每一个图形都是由一些同样大小的三角形按一定的规律排列组成的，其中第①个图形中有5个小三角形，第②个图形中有10个小三角形，第③个图形中有16个小三角形，按此规律，则第⑨个图中小三角形的个数是（ ）
A．69B．73C．77D．83
【变式训练2】如图，第（1）个多边形由正三角形“扩展”而来，边数记为，第（2）个多边形由正方形“扩展”而来，边数记为，……，依此类推，由正n边形“扩展”而来的多边形的边数记为，当的结果是时，n的值为 ．
【变式训练3】观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…，则第15个图形中有 个三角形．
课后训练
1．我们把称为有理数的差倒数，如：2的差倒数是，-2的差倒数是．如果，是的差倒数，是的差倒数，是的差倒数，…，依此类推，那么的值是（ ）
A．−B．−3C．D．
2．如图是由边长为1的木条组成的几何图案，观察图形规律，第一个图案由1个正方形组成，共用的木条根数S1＝4，第二个图案由4个正方形组成，共用的木条根数S2＝12，第三个图案由9个正方形组成，共用的木条根数S3＝24，以此类推…那么第100个图案共用的木条根数S100为（ ）
A．19600B．20400C．20200D．20000
3．按如图所示的规律搭正方形：搭一个小正方形需要4根小棒，搭两个小正方形需要
17．观察下列一串单项式的特点： ， ， ， ， ，…
（1）写出第10个和第2020个单项式．
（2）写出第n个单项式．
4．由于（﹣1）n＝，所以我们通常把（﹣1）n称为符号系数．
（1）观察下列单项式：﹣，…按此规律，第5个单项式是 ，第n个单项式是 ．
（2）的值为 ；
（3）你根据（2）写出一个当n为偶数时值为2，当n为奇数时值为0的式子 ．
5．图1由若干个小圆圈组成的一个形如正三角形的图案，第1层有1个圆圈，每一层都比上一层多1个圆圈，一共堆了n层．
（1）如图1所示，第100层有 个小圆圈，从第1层到第n层共有 个小圆圈；
（2）我们自上往下按图2的方式排列一串连续的正整数1，2，3，…，则第20层的第5个数是 ；
（3）我们自上往下按图3的方式排列一串整数31，﹣33，35，﹣37，…，则求从第1层到第20层的所有数的绝对值的和 ．
专题06 整式中规律探索的三种考法
类型一、单项式规律性问题
例．有一列式子，按一定规律排列成，，，，，…，第n个式子为 （n为正整数）．
【答案】
【分析】通过观察发现：每项前面的系数是前一项的系数乘以，每一项的次数是．
【详解】解：每项前面的系数是前一项的系数乘以，
∴第n项的系数是，
每一项的次数是，
∴第n个式子为．
故答案是：．
【点睛】本题考查找规律，解题的关键是能够找出这列式子的规律．
【变式训练1】观察下列单项式：按此规律，可以得到第2020个单项式是 ．
【答案】
【分析】根据已知单项式归纳类推出一般规律，由此即可得．
【详解】第1个单项式为，
第2个单项式为，
第3个单项式为，
第4个单项式为，
第5个单项式为，
归纳类推得：第n的单项式为，其中n为正整数，
则第2020个单项式为，
故答案为：．
【点睛】本题考查了单项式规律题，观察已知单项式，正确归纳类推出一般规律是解题关键．
【变式训练2】有一组单项式依次为根据它们的规律，第个单项式为 ．
【答案】或
【分析】根据观察，可发现第n个单项式的分母为，分子为．
【详解】解：通过观察可发现第n个单项式的分母为，分子为，故第n个单项式为，还可以写成．
故答案为：或．
【点睛】本题考查的知识点是探寻单项式的排列规律，根据所给数据总结归纳出数据的排列规律是解此题的关键．
类型二、数字类规律探索
例．如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点．若青蛙从数1这点开始跳，第1次跳到数3那个点，如此，则经2015次跳后它停的点所对应的数为 （ ）
A．5B．3C．2D．1
【答案】C
【分析】先根据题意，求出前几次跳到的点的位置，发现这是一个循环，按照3、5、2、1成一个循环，再用解循环问题的方法求解．
【详解】解：按照题意，第一次在1这个点，下一次就跳到3，再下一次跳到5，再下一次跳到2，2是偶数了，就逆时针跳一个点，又回到了1这个点，
发现这是一个循环，3、5、2、1是一个循环，
，
∴最后到2这个点．
故选：C．
【点睛】本题考查找规律，解题的关键是通过前几个数发现这是一个循环问题，利用解循环问题的方法求解．
【变式训练1】按上面数表的规律．得下面的三角形数表：
（1）上表中，第九行有 个算式，第九行最中间的算式是 ．
（2）把下表中的数从小到大排成一列数：3，5，6，9，10，12，…则第15个数是 ，
【答案】 ，
【分析】（1）根据规律第9行有9个数，每一个算式的第二个加数都是，第个数即为中间的数，第一个加数按照1，2，，，，写出即可求解．
（2）根据规律写出第行的数的表达式，再根据每一行的数的个数与行数相同，求出第个数是第行的最后一个数，然后把代入进行计算即可得解；
【详解】（1）观察可得，第9行有9个数，每一个算式的第二个加数都是，第个数即为中间的数，第一个加数按照1，2，，，，
∴第九行有个算式，第九行最中间的算式是
故答案为：，；
（2）根据规律，第n行的数为：
∵第1行有1个数，第2行有2个数，第3行有3个数，…，第行有个数，
∵
∴第15个数是第5行第5个数，即
故答案为：．
【点睛】本题考查数字变化规律探究，根据指数的变化特点写出第行排列的各数是解题的关键．
【变式训练2】将正整数按如图所示的规律排列，有序数对表示第排，从左到右第个数．如有序数对表示8，则有序数对表示的数为 ．
【答案】123
【分析】有序数对表示第排，从左到右第个数．则前n排的数字共有个数，将n=16代入，可得出第16行有16个数，第1个数是136，从大到小排列，据此解答即可．
【详解】解：由图可知，
第一排1个数，
第二排2个数，数字从大到小排列，
第三排3个数，数字从小到大排列，
第四排4个数，数字从大到小排列，
…，
则前n排的数字共有个数，
∵当n=16时，，
∴第16行有16个数，第1个数是136，从大到小排列，
∴第16行第14个数是123，
故选：C．
故答案为：123．
【点睛】此题考查对数字变化类知识点的理解和掌握，解答此类题目的关键是根据题目中给出的图形、数值、数列等已知条件，认真分析，找出规律，解决问题．
【变式训练3】斐波那契数列因意大利数学家斐波那契以兔子繁殖为例引入，故又称为“兔子数列”，即：1，1，2，3，5，8，13，21，34，…实际生活中及现代物理与化学等领域也有着广泛的应用，若斐波那契数列中的第n个数记为，则与斐波那契数列中的第 个数相同．
【答案】2022
【分析】由于斐波那契数列中的前两个数均为1，故数列中的1可记作a2，这样，，…，依次化简，结论可得．
【详解】解：∵斐波那契数列中，
∴1=，
∴
……
故答案为：2022.
【点睛】本题主要考查了数字变化的规律，数学常识，准确找出数字变化的规律是解题的关键．
【变式训练4】观察下列一组数：2，，，…，它们按一定规律排列，第n个数记为，且满足．则 ， ．
【答案】
【分析】由题意推导可得an=，即可求解．
【详解】解：由题意可得：a1=2=，a2=，a3=，
∵，∴2+=7，
∴a4=，
∵，
∴a5=，
同理可求a6=，
∴an=，
∴a2022=，
故答案为：，．
【点睛】本题考查了数字的变化类，找出数字的变化规律是解题的关键．
类型三、图形类规律探索
例.根小棒，搭2020个这样的小正方形需要小棒（ ）根．
A．8080B．6066C．6061D．6060
【答案】C
【分析】通过归纳与总结得出规律：每增加1个正方形，火柴棒的数量增加3根，由此求出第n个图形时需要火柴的根数的代数式，然后代入求值即可．
【详解】解：搭2个正方形需要4+3×1＝7根火柴棒；
搭3个正方形需要4+3×2＝10根火柴棒；
搭n个这样的正方形需要4+3（n﹣1）＝3n+1根火柴棒；
∴搭2020个这样的正方形需要3×2020+1＝6061根火柴棒；
故选C．
【点睛】本题考查了图形规律型：图形的变化．解题的关键是发现各个图形的联系，找出其中的规律，有一定难度，要细心观察总结．
【变式训练1】下列每一个图形都是由一些同样大小的三角形按一定的规律排列组成的，其中第①个图形中有5个小三角形，第②个图形中有10个小三角形，第③个图形中有16个小三角形，按此规律，则第⑨个图中小三角形的个数是（ ）
A．69B．73C．77D．83
【答案】B
【分析】根据已知图形得出第⑨个图形中三角形的个数的特点，据此可得答案．
【详解】解：∵第①个图形中三角形的个数5=1+2×（1-1），
第②个图形中三角形的个数10=5+2×1+3，
第③个图形中三角形的个数16=5+2×2+3+4，
第④个图形中三角形的个数23=5+2×3+3+4+5，
第⑤个图形中三角形的个数31=5+2×4+3+4+5+6，
……
第⑨个图形中三角形的个数为5+2×8+3+4+5+6+7+8+9+10=73
第n个图形中三角形的个数为5+2×(n-1)+3+4……+(n+1)（n>1）
故选：B．
【点睛】本题主要考查图形的变化规律，解题的关键是得出每次变换增加个数规律,列出代数式．
【变式训练2】如图，第（1）个多边形由正三角形“扩展”而来，边数记为，第（2）个多边形由正方形“扩展”而来，边数记为，……，依此类推，由正n边形“扩展”而来的多边形的边数记为，当的结果是时，n的值为 ．
【答案】673
【分析】结合图形观察数字，发现：，，，进一步得到，代入进行裂项，即可求解．
【详解】解：结合图形观察数字，发现：，，，进一步得到，
∴
，
解得，
故答案为：673．
【点睛】此题考查了图形的变化规律题，注意从特殊推广到一般是解题关键．
【变式训练3】观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…，则第15个图形中有 个三角形．
【答案】57
【分析】根据每个图形增加三角形的个数，找到规律即可．
【详解】解：第1个图形中一共有1个三角形，
第 2个图形中一共有1+4=5个三角形，
第 3个图形中一共有1+4+4=9个三角形，
…，
第n个图形中三角形的个数是1+4（n﹣1）=（4n﹣3）个，
当n=15时，4n﹣3=4×15﹣3=57．
故答案为：57．
【点睛】本题考查了图形的变化规律，解题关键是通过图形数量的变化发现规律，并应用规律解决问题．
课后训练
1．我们把称为有理数的差倒数，如：2的差倒数是，-2的差倒数是．如果，是的差倒数，是的差倒数，是的差倒数，…，依此类推，那么的值是（ ）
A．−B．−3C．D．
【答案】D
【分析】根据“差倒数”的定义，写出前几个数，从而可以发现数字的变化规律，然后即可求得所求式子的值．
【详解】解：由题意可得，
，
，
，
，
…，
则这列数每三个数一个循环．
∵2020÷6=336……4，
∴

．
故选：D．
【点睛】本题考查数字类的变化规律，解答本题的关键是明确题意，发现数字的变化特点，求出所求式子的值．
2．如图是由边长为1的木条组成的几何图案，观察图形规律，第一个图案由1个正方形组成，共用的木条根数S1＝4，第二个图案由4个正方形组成，共用的木条根数S2＝12，第三个图案由9个正方形组成，共用的木条根数S3＝24，以此类推…那么第100个图案共用的木条根数S100为（ ）
A．19600B．20400C．20200D．20000
【答案】C
【分析】本题要通过第1、2、3和4个图案找出普遍规律，进而得出第n个图案的规律为Sn＝4n＋2n×（n−1），得出结论即可．
【详解】解：观察图形可知：
第1个图案由1和小正方形组成，共用的木条根数S1＝4×1，即S1＝4×1＋2×1×（1−1）；
第2个图案由4个小正方形组成，共用的木条根数S2＝4×2＋2×2；即S1＝4×2＋2×2×（2−1）；
第3个图案由9个小正方形组成，共用的木条根数S3＝4×3＋2×3；即S1＝4×3＋2×3×（3−1）；
第4个图案由16个小正方形组成，共用的木条根数S4＝4×4＋2×4；即S1＝4×4＋2×4×（4−1）；
…
由此发现规律是：
第n个图案由n2个小正方形组成，共用的木条根数Sn＝4n＋2n×（n−1），
当n＝100时，S100＝4×100＋200×（100−1）＝20200，
故选：C．
【点睛】本题考查图形变换找规律的问题，熟练找出前四个图形的规律是解题个关键．
3．按如图所示的规律搭正方形：搭一个小正方形需要4根小棒，搭两个小正方形需要
17．观察下列一串单项式的特点： ， ， ， ， ，…
（1）写出第10个和第2020个单项式．
（2）写出第n个单项式．
【答案】（1）﹣19x10y，﹣4039x2020y；（2）(﹣1)n+1(2n﹣1)xny．
【分析】（1）通过观察题意可得：10为偶数，单项式的系数为负数，是﹣19，x的指数为10，y的指数不变，还是1，由此可得出第10个单项式，同理第2020个单项式也可由此得出；
（2）通过观察题意可得：n为奇数时，单项式的系数为正数，n为偶数时，单项式的系数为负数．系数的数字部分是连续的奇数，可用2n﹣1来表示，第n个单项式的x的指数为n，y的指数不变，还是1，由此可解出本题．
【详解】解：（1）∵当n＝1时，xy，
当n＝2时，﹣3x2y，
当n＝3时，5x3y，
当n＝4时，﹣7x4y，
当n＝5时，9x5y，
∴第10个单项式是﹣(2×10﹣1) x10y，即﹣19x10y．
第2020个单项式是﹣(2×2020﹣1) x2020y，即﹣4039x2020y．
故答案为：﹣19x10y，﹣4039x2020y．
（2）∵n为奇数时，单项式的系数为正数，n为偶数时，单项式的系数为负数．
∴符合可用(﹣1)n+1表示，
∵系数的数字部分是连续的奇数，
∴可用2n﹣1来表示，
又∵第n个单项式的x的指数为n，y的指数不变，还是1，
∴第n个单项式可表示为(﹣1)n+1(2n﹣1)xny．
故答案为：(﹣1)n+1(2n﹣1)xny．
【点睛】本题考查的是单项式，根据题意找出各式子的规律是解答此题的关键．
4．由于（﹣1）n＝，所以我们通常把（﹣1）n称为符号系数．
（1）观察下列单项式：﹣，…按此规律，第5个单项式是 ，第n个单项式是 ．
（2）的值为 ；
（3）你根据（2）写出一个当n为偶数时值为2，当n为奇数时值为0的式子 ．
【答案】（1）， ；（2）b或a；（3）1+（﹣1）n．
【分析】（1）观察发现，奇数项为负，偶数项为正，系数的分子与项数相同，系数的分母的规律是4n2﹣1，字母x的指数与项数相同，据此可解；
（2）分n为奇数和n为偶数两种情况来计算即可；
（3）取指数为n的项的底数与不含n的项互为相反数，则不难得出答案．
【详解】（1）观察下列单项式：，…按此规律，第5个单项式是，第n个单项式是
故答案为：，．
（2）n为奇数时， ，
n为偶数时，.故答案为：b或a．
（3）可以这样写一个当n为偶数时值为2，当n为奇数时值为0的式子：1+（﹣1）n．
故答案为：1+（﹣1）n．
【点睛】此题考查单项式规律的探究，观察并发现数字间的规律是解题的关键.
5．图1由若干个小圆圈组成的一个形如正三角形的图案，第1层有1个圆圈，每一层都比上一层多1个圆圈，一共堆了n层．
（1）如图1所示，第100层有 个小圆圈，从第1层到第n层共有 个小圆圈；
（2）我们自上往下按图2的方式排列一串连续的正整数1，2，3，…，则第20层的第5个数是 ；
（3）我们自上往下按图3的方式排列一串整数31，﹣33，35，﹣37，…，则求从第1层到第20层的所有数的绝对值的和 ．
【答案】（1）100， ；（2）195；（3）50400．
【分析】（1）观察图1发现规律：第n层有n个小圆圈，从第1层到第n层共有圆圈的个数为1+2+3+…+n，计算即可得圆圈的个数，进而可得结论；
（2）观察图2发现规律：从1开始的自然数列，第n层放n个，进而可得第20层第5个数；
（3）观察图3发现规律：第n层放n个，从第1个数开始，符号“+﹣”周期变化，绝对值依次加2，可得第20层最后一个数的绝对值，最后得第1层到第20层所有数的绝对值和．
【详解】解：（1）图1规律：第n层有n个小圆圈，则第100层有100个小圆圈，
因为1+2+3+…+n＝．
所以从第1层到第n层共有个小圆圈；
故答案为：100，；
（2）图2规律：从1开始的自然数列，第n层放n个，则第20层第5个数为：
1+2+3+…+19+5＝195．
故答案为：195；
（3）图3规律：第n层放n个，从第1个数开始，符号“+﹣”周期变化，绝对值依次加2，
则第20层最后一个数的绝对值为：
31+（2+3+4+…+20）×2＝449，
则第1层到第20层所有数的绝对值和为：
31+33+35+…+449＝50400．
故答案为：50400．
【点睛】本题考查了根据图形的变化规律列式，计算等知识，理解图形的变化规律，并寻找其中规律是解题关键．