
人教版八年级数学上册专题07三角形中的特殊模型-平分平行(射影)构等腰、角平分线第二定理模型(原卷版+解析)
展开平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型)
模型1、平分平行(射影)构等腰
1)角平分线加平行线必出等腰三角形.
模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。 (简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1 图2 图3
条件:如图1,OO’平分∠MON,过OO’的一点P作PQ//ON. 结论:△OPQ是等腰三角形。
条件:如图2,△ABC中,BD是 ∠ ABC的角平分线,DE ∥ BC。结论:△BDE是等腰三角形。
条件:如图3,在中,平分,平分,过点O作的平行线与,分别相交于点M,N.结论:△BOM、△CON都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.
→ 图4
条件:如图4,BE平分∠CBA,∠ACB=∠CDA=90°. 结论:三角形CEF是等腰三角形。
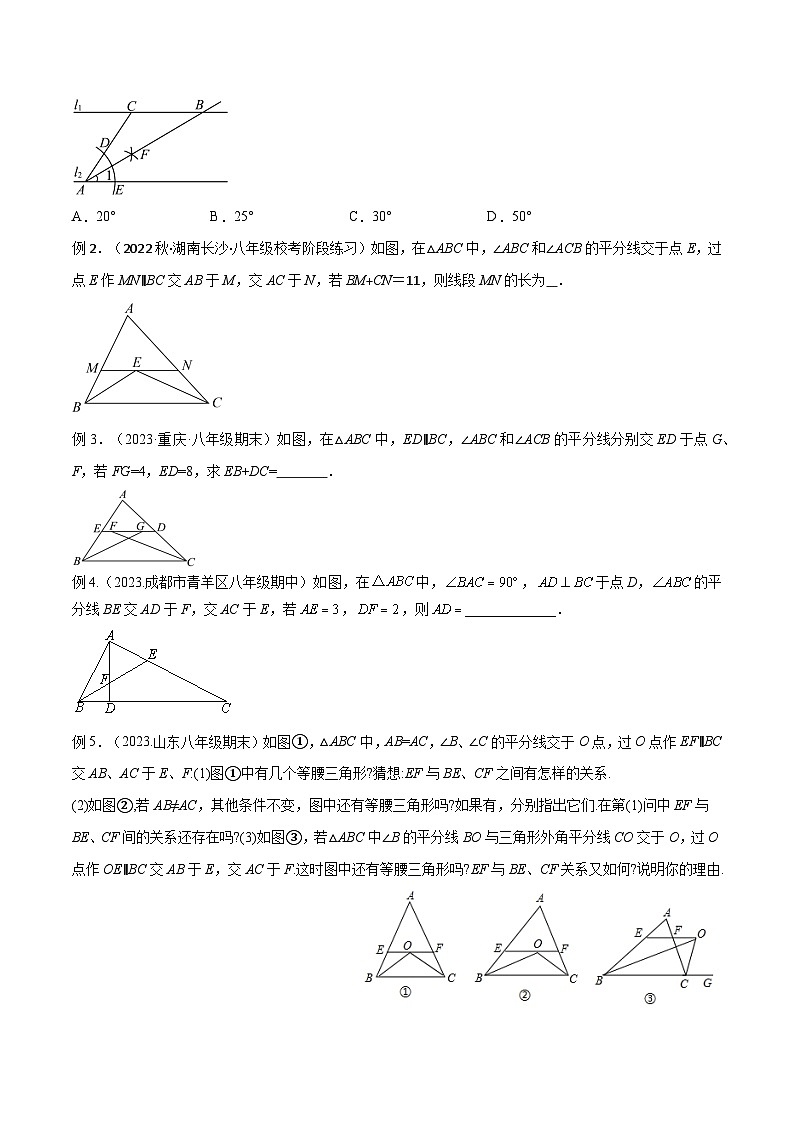
例1.(2023春·海南·八年级统考期末)如图,直线,点C、A分别、上,以点A为圆心,适当长为半径画弧,交、于点D、E;分别以D、E为圆心,大于长为半径画弧,两弧交于点F;作射线交于点B.若,则的度数为( )
A.20°B.25°C.30°D.50°
例2.(2022秋·湖南长沙·八年级校考阶段练习)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=11,则线段MN的长为 .
例3.(2023·重庆·八年级期末)如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=4,ED=8,求EB+DC= .
例4.(2023.成都市青羊区八年级期中)如图,在中,,于点D,的平分线BE交AD于F,交AC于E,若,,则_____________.
例5.(2023.山东八年级期末)如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
模型2、角平行线第二定理(内角平分线定理和外角平分线定理)模型
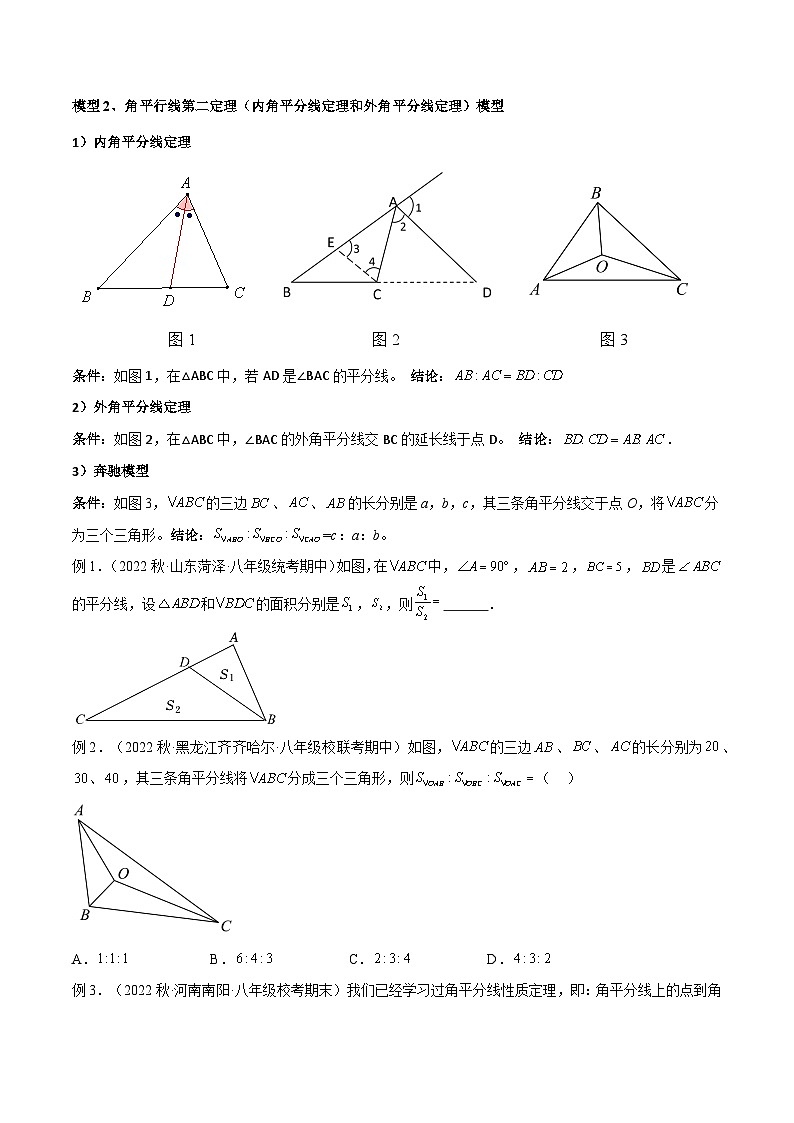
1)内角平分线定理
图1 图2 图3
条件:如图1,在△ABC中,若AD是∠BAC的平分线。 结论:
2)外角平分线定理
条件:如图2,在△ABC中,∠BAC的外角平分线交BC的延长线于点D。 结论:.
3)奔驰模型
条件:如图3,的三边、、的长分别是a,b,c,其三条角平分线交于点O,将分为三个三角形。结论:=c:a:b。
例1.(2022秋·山东菏泽·八年级统考期中)如图,在中,,,,是的平分线,设和的面积分别是,,则 .
例2.(2022秋·黑龙江齐齐哈尔·八年级校联考期中)如图,的三边、、的长分别为、、,其三条角平分线将分成三个三角形,则( )
A.B.C.D.
例3.(2022秋·河南南阳·八年级校考期末)我们已经学习过角平分线性质定理,即:角平分线上的点到角两边的距离相等.如图,已知的角平分线BD交边AC于点D.
(1)求证:=(2)求证:=;(3)如果BC=4,AB=6,AC=5,那么CD=______.
例4、△ABC中,∠BAC的外角平分线交BC的延长线于点D,求证:.
例5.(2022秋·北京·八年级校考期中)在中,D是边上的点(不与点B、C重合),连接.
(1)如图1,当点D是边的中点时,_____;
(2)如图2,当平分时,若,,求的值(用含m、n的式子表示);
(3)如图3,平分,延长到E.使得,连接,若,求的值.
课后专项训练
1.(2023春·山东淄博·九年级校考期中)如图,中,,点I为各内角平分线的交点,过I点作的垂线,垂足为H,若,,,那么的值为( )
A.1B.C.2D.
2.(2022秋·山东聊城·八年级校联考期中)如图,在中,,,是的平分线,设和的面积分别是,,则的值为( )
A.B.C.D.
3.(2023秋·云南楚雄·八年级统考期末)如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A.B.C.D.
4.(2023·广东广州·八年级校考阶段练习)如图,是的角平分线,、分别是和的高,下列说法中正确的有( )个.
1)垂直平分;2);3);4)四边形的面积是面积的一半
A.1B.2C.3D.4
5.(2023春·湖南岳阳·八年级统考期末)如图,是的角平分线,相交于点于,,下列四个结论:①;②;③若的周长为,则;④若,则.其中正确的结论有( )个.
A.B.C.D.
6.(2023春·山东·七年级专题练习)如图,中,与的平分线交于点,过点作交于点,交于点,那么下列结论:
①和都是等腰三角形;②;③;④若,则.
其中正确的有( )个
A.1B.2C.3D.4
7.(2023·广东·八年级期中)如图,已知,平分,,则( )
A.105°B.120°C.130°D.150°
8.(2023秋·四川南充·八年级校考期末)如图,内角和外角的平分线交于点,交于点,过点作交于点,交于点,连接,有以下结论;①;②;③若,则;④;⑤.其中正确的结论有( )
A.1个B.2个C.3个D.4个
9.(2023春·全国·七年级专题练习)如图,在中,已知和的平分线相交于点F,过点F作,交于D,交于E,若,则的周长为( )
A.6B.8C.10D.12
10.(2022秋·江苏宿迁·八年级校考期末)如图,在中,,垂足为D,平分,交于点E,交于点F.若,则的长为( )
A.B.3C.D.
11.(2023春·四川达州·八年级校考阶段练习)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,则下列结论成立的是( )
A.EC=EFB.FE=FCC.CE=CFD.CE=CF=EF
12.(2023·成都市·八年级期中)如图,△ABC中,BD是 ∠ ABC的角平分线,DE ∥ BC,交AB 于 E,∠A=60º, ∠BDC=95º,则∠BED的度数是( )
A.35°B.70°C.110°D.130°
13.(2023春·陕西咸阳·八年级咸阳市秦都中学校考阶段练习)如图,在中,,点为的边上一点,点分别在边上,连接,若,则的度数为 .
14.(2023秋·安徽滁州·八年级统考期末)中,D是边上的点(不与点B,C重合),连接.
(1)如图1,当平分时,若,,则 ;
(2)如图2,平分,延长到E,使得,连接,如果,,,则 .
15.(2022秋·天津·八年级校考期中)如图,在中,是的平分线,延长至E,使,若,的面积为9,则的面积是 .
16.(2022秋·湖北荆门·八年级统考期末)如图,在中,于点D,G是延长线上一点,平分,且,E是上一点,连接并延长交于点F.
(1)求证:;(2)猜想并证明:当E在何处时,.
17.(2023·浙江八年级课时练习)如图,已知、的平分线相交于点,过点且.
(1)若,,求的度数;
(2)若,,求、的度数.
18.(2023广东江门八年级月考)(1)如图1,已知,在中,,平分,平分,过点作,分别交、于、两点,则图中共有________个等腰三角形:与、之间的数量关系是________,的周长是________.
(2)如图2,若将(1)中“中,”改为“若为不等边三角形,,”其余条件不变,则图中共有________个等腰三角形;与、之间的数量关系是什么?证明你的结论,并求出的周长.
(3)已知:如图3,在外,,且平分,平分的外角,过点作,分别交、于、两点,则与、之间又有何数量关系呢?写出结论并证明.
19.(2023·吉林·八年级校考期末)【教材呈现】如图是华师版八年级上册数学教材第96页的部分内容.
【定理证明】结合图①,“角平分线的性质定理”证明过程中.运用了与全等,全等最直接的依据是
【定理感知】如果教材中的已知条件不变,如图①,当,时,则面积为 .
【定理应用】如图②,在中,平分交于点D.求证:
【拓展应用】如图③,在中,,,,将先沿的平分线折叠,再剪掉重叠部分(即四边形),再将余下部分沿的平分线折叠,再剪掉重叠部分,直接写出剩余的的面积为 .
20.(2022秋·福建厦门·八年级厦门市湖里中学校考期中)如图,为的角平分线.
(1)如图1,若于点,交于点,,.则________;
(2)如图2,若,,的面积是10,求的面积;
(3)如图3,若,,,请直接写出的长(用含,的式子表示)
专题07.三角形中的特殊模型-平分平行(射影)构等腰、角平分线第二定理模型
角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型)
模型1、平分平行(射影)构等腰
1)角平分线加平行线必出等腰三角形.
模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。 (简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1 图2 图3
条件:如图1,OO’平分∠MON,过OO’的一点P作PQ//ON. 结论:△OPQ是等腰三角形。
条件:如图2,△ABC中,BD是 ∠ ABC的角平分线,DE ∥ BC。结论:△BDE是等腰三角形。
条件:如图3,在中,平分,平分,过点O作的平行线与,分别相交于点M,N.结论:△BOM、△CON都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.
→ 图4
条件:如图4,BE平分∠CBA,∠ACB=∠CDA=90°. 结论:三角形CEF是等腰三角形。
例1.(2023春·海南·八年级统考期末)如图,直线,点C、A分别、上,以点A为圆心,适当长为半径画弧,交、于点D、E;分别以D、E为圆心,大于长为半径画弧,两弧交于点F;作射线交于点B.若,则的度数为( )
A.20°B.25°C.30°D.50°
【答案】C
【分析】根据作图可知平分,根据平行线的性质,求出的度数,即可得解.
【详解】解:∵,,∴,
由作图可知:平分,∴,故选C.
【点睛】本题考查平行线的性质,基本作图—作角平分线.解题的关键是根据作图方法,得到平分.
例2.(2022秋·湖南长沙·八年级校考阶段练习)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=11,则线段MN的长为 .
【答案】11
【分析】根据平行线的性质得出∠MEB=∠EBC,∠NEC=∠ECB,根据角平分线定义得出∠MBE=∠EBC,∠NCE=∠ECB,求出∠MEB=∠MBE,∠NEC=∠NCE,推出ME=BM,EN=CN即可.
【详解】解:∵MN∥BC,∴∠MEB=∠EBC,∠NEC=∠ECB,
∵∠ABC和∠ACB的平分线交于点E,∴∠MBE=∠EBC,∠NCE=∠ECB,
∴∠MEB=∠MBE,∠NEC=∠NCE,∴ME=BM,EN=CN,
∵BM+CN=11,∴EM+EN=11,即MN=11,答案为:11.
【点睛】本题考查了等腰三角形的判定、平行线的性质、角平分线定义等知识点,能求出ME=BM和EN=CN是解此题的关键.
例3.(2023·重庆·八年级期末)如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=4,ED=8,求EB+DC= .
【答案】12
【分析】由角平分线与平行线易得∠EBG=∠EGB,从而得到EB=EG,同理可得DF=DC,再根据EB+DC=EG+DF=ED+FG即可得答案.
【详解】∵BG平分∠EBC∴∠EBG=∠GBC
∵ED∥BC∴∠EGB=∠GBC∴∠EBG=∠EGB ∴EB=EG 同理可得DF=DC
∴EB+DC=EG+DF=ED+FG=8+4=12故答案为:12.
【点睛】本题考角平分线与平行线,掌握角平分线加平行线,可得等腰三角形这一几何模型是解题的关键.
例4.(2023.成都市青羊区八年级期中)如图,在中,,于点D,的平分线BE交AD于F,交AC于E,若,,则_____________.
【答案】5
【详解】由角度分析易知,即,
∵ ∴ ∵ ∴
【点睛】这道题主要讲解角平分线加射影模型必出等腰三角形的模型.
例5.(2023.山东八年级期末)如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
【答案】(1)△AEF、△OEB、△OFC、△OBC、△ABC共5个,EF=BE+FC;(2)有,△EOB、△FOC,存在;(3)有,EF=BE-FC.
【分析】(1)由AB=AC,可得∠ABC=∠ACB;又已知OB、OC分别平分∠ABC、∠ACB;故∠EBO=∠OBC=∠FCO=∠OCB;根据EF∥BC,可得:∠OEB=∠OBC=∠EBO,∠FOC=∠FCO=∠BCO;由此可得出的等腰三角形有:△AEF、△OEB、△OFC、△OBC、△ABC;
已知了△EOB和△FOC是等腰三角形,则EO=BE,OF=FC,则EF=BE+FC.
(2)由(1)的证明过程可知:在证△OEB、△OFC是等腰三角形的过程中,与AB=AC的条件没有关系,故这两个等腰三角形还成立.所以(1)中得出的EF=BE+FC的结论仍成立.
(3)思路与(2)相同,只不过结果变成了EF=BE-FC.
【详解】解:(1)图中是等腰三角形的有:△AEF、△OEB、△OFC、△OBC、△ABC;
EF、BE、FC的关系是EF=BE+FC.理由如下:
∵AB=AC,∴∠ACB=∠ABC,△ABC是等腰三角形;
∵BO、CO分别平分∠ABC和∠ACB,∴∠ABO=∠OBC=∠ABC,∠OCB=∠ACO=∠ACB,
∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,∴∠ABO=∠OBC=∠EOB=∠OCB=∠FOC=∠FCO,
∴△EOB、△OBC、△FOC都是等腰三角形,
∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,∴∠AEF=∠AFE,∴△AEF是等腰三角形,
∵OB、OC平分∠ABC、∠ACB,∴∠ABO=∠OBC,∠ACO=∠OCB;
∵EF∥BC,∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO;
即EO=EB,FO=FC;∴EF=EO+OF=BE+CF;
(2)当AB≠AC时,△EOB、△FOC仍为等腰三角形,(1)的结论仍然成立.
∵OB、OC平分∠ABC、∠ACB,∴∠ABO=∠OBC,∠ACO=∠OCB;
∵EF∥BC,∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO;
即EO=EB,FO=FC;∴EF=EO+OF=BE+CF;
(3)△EOB和△FOC仍是等腰三角形,EF=BE-FC.理由如下:
同(1)可证得△EOB是等腰三角形;∵EO∥BC,∴∠FOC=∠OCG;
∵OC平分∠ACG,∴∠ACO=∠FOC=∠OCG,
∴FO=FC,故△FOC是等腰三角形;∴EF=EO-FO=BE-FC.
【点睛】本题主要考查了等腰三角形的判定和性质,平行线、角平分线的性质等知识.进行线段的等量代换是正确解答本题的关键.
模型2、角平行线第二定理(内角平分线定理和外角平分线定理)模型
1)内角平分线定理
图1 图2 图3
条件:如图1,在△ABC中,若AD是∠BAC的平分线。 结论:
2)外角平分线定理
条件:如图2,在△ABC中,∠BAC的外角平分线交BC的延长线于点D。 结论:.
3)奔驰模型
条件:如图3,的三边、、的长分别是a,b,c,其三条角平分线交于点O,将分为三个三角形。结论:=c:a:b。
例1.(2022秋·山东菏泽·八年级统考期中)如图,在中,,,,是的平分线,设和的面积分别是,,则 .
【答案】/
【分析】过点D作于E,根据角平分线的性质得出,再根据三角形的面积公式得出与即可求解.
【详解】解:如图,过点D作于E,
∵,,是的角平分线,∴,
∵,,∴,故答案为:.
【点睛】本题考查角平分线的性质,三角形的面积公式,根据角平分线的性质得出是解题的关键.
例2.(2022秋·黑龙江齐齐哈尔·八年级校联考期中)如图,的三边、、的长分别为、、,其三条角平分线将分成三个三角形,则( )
A.B.C.D.
【答案】C
【分析】过点分别作,,的垂线,可得,从而可证,即可求解.
【详解】解:如图,过点分别作,,的垂线,垂足分别为点,,,
由角平分线的性质定理得:,的三边,,长分别是,,,
∴.故选:C.
【点睛】本题考查了角平分线的性质定理,掌握定理是解题的关键.
例3.(2022秋·河南南阳·八年级校考期末)我们已经学习过角平分线性质定理,即:角平分线上的点到角两边的距离相等.如图,已知的角平分线BD交边AC于点D.
(1)求证:=(2)求证:=;(3)如果BC=4,AB=6,AC=5,那么CD=______.
【答案】(1)见解析(2)见解析(3)2
【分析】(1)作,作DHAB,根据角平分线的性质可得DF=DH,继而根据三角形面积公式进行求解即可得;(2)作BECA,继而根据三角形面积公式进行求解即可得;
(3)由(2)可得= ,结合已知可得AD=AC-CD,代入相关数据进行求解即可得.
【详解】(1)作,作DHAB垂足分别为F,H
∵BD是的角平分线. ∴DF=DH 则有:= =
(2)作BECA垂足为E
则有: = = ∴=
(3)由(2)知,= BC=4,AB=6,AC=5,
故答案为:2
【点睛】本题考查角平分线的性质、三角形面积等知识,是基础考点,掌握相关知识是解题关键.
例4、△ABC中,∠BAC的外角平分线交BC的延长线于点D,求证:.
证明:过C作AD的平行线交AB于点E.
∵ ∴,∠1=∠3,∠2=∠4
∵AD为∠BAC的外角平分线 ∴∠1=∠2 ∴∠3=∠1=∠2=∠4
∴AE=AC ∴
例5.(2022秋·北京·八年级校考期中)在中,D是边上的点(不与点B、C重合),连接.
(1)如图1,当点D是边的中点时,_____;
(2)如图2,当平分时,若,,求的值(用含m、n的式子表示);
(3)如图3,平分,延长到E.使得,连接,若,求的值.
【答案】(1)(2)(3)16
【分析】(1)过A作于E,根据三角形面积公式求出即可;
(2)过D作于E,于F,根据角平分线性质求出,根据三角形面积公式求出即可;(3)根据已知和(1)(2)的结论求出和的面积,即可求出答案.
【详解】(1))过A作于E,∵点D是边上的中点,∴,
∴故答案为:;
(2)过D作于E,于F,∵为的角平分线,∴,
∵,,∴;
(3)∵,∴由(1)知:,∵,∴,
∵,平分,∴由(2)知:,
∴,∴,故答案为:16.
【点睛】本题考查了角平分线性质和三角形的面积公式,能根据(1)(2)得出规律是解此题的关键.
课后专项训练
1.(2023春·山东淄博·九年级校考期中)如图,中,,点I为各内角平分线的交点,过I点作的垂线,垂足为H,若,,,那么的值为( )
A.1B.C.2D.
【答案】A
【分析】连接、、,过I作于M,于N,利用角平分线的性质,以及等积法求线段的长度,即可得解.
【详解】解:连接、、,过I作于M,于N,
∵点I为各内角平分线的交点,,,,∴,
∵,,,∴,
∵,∴,
∵,,,,∴,故A正确.故选:A.
【点睛】本题主要考查角平分线的性质,等积法求线段长度.熟练掌握角平分线的性质,利用等积法求线段的长度是解题的关键.
2.(2022秋·山东聊城·八年级校联考期中)如图,在中,,,是的平分线,设和的面积分别是,,则的值为( )
A.B.C.D.
【答案】B
【分析】过D点作于E,根据角平分线的性质得到,然后利用三角形的面积公式求的值.
【详解】解:过D点作于E,如图,
∵是的平分线,,,∴,
∴.故选:B.
【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
3.(2023秋·云南楚雄·八年级统考期末)如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A.B.C.D.
【答案】C
【分析】过点作,,,垂足分别为,,,根据角平分线的性质可知:,利用三角形的面积公式计算可求解.
【详解】解:过点作,,,垂足分别为,,,
的三条角平分线交于点,,在中,,,,
,故选:C.
【点睛】本题考查三角形的面积,角平分线的性质,利用角平分线的性质求得是解题的关键.
4.(2023·广东广州·八年级校考阶段练习)如图,是的角平分线,、分别是和的高,下列说法中正确的有( )个.
1)垂直平分;2);3);4)四边形的面积是面积的一半
A.1B.2C.3D.4
【答案】B
【分析】根据角平分线的性质、三角形的面积公式和全等三角形的判定与性质依次分析判断即可.
【详解】解:∵、分别是和的高,∴,
∵平分,∴,故(2)正确;
∴,
又∵,∴,即,故(3)正确
∵,∴,∴,∴垂直平分,
但由于不一定是直角,则条件不足以判定垂直平分,故(1)不一定成立;
∵,,
∵不一定等于,故(4)不一定成立;故选:B.
【点睛】本题考查了角平分线的性质、三角形的面积公式和全等三角形的判定与性质,解题关键是牢记相关概念 与性质,正确分析推理.
5.(2023春·湖南岳阳·八年级统考期末)如图,是的角平分线,相交于点于,,下列四个结论:①;②;③若的周长为,则;④若,则.其中正确的结论有( )个.
A.B.C.D.
【答案】C
【分析】根据三角形内角和定理可验证结论①;如图所示,在上截取,可证,,根据全等三角形的性质可验证结论②;如图所示,连接,过点分别作于点,作于点,根据角平分线的性质,三角形的面积计算方法可验证结论③;结合结论②,③,图形结合,等面积法等知识可验证结论④.
【详解】解:结论①,
∵,,∴,
∵是的角平分线,∴,,
∴,在中,,
∴,故结论①正确;
结论②,由结论①正确可知,,
∵,∴,
∵,∴,如图所示,在上截取,
∵是的角平分线,∴,
∴在中,,∴,
∴,∴,
∴,,∴在中,
,∴,∴,
∴,故结论②正确;结论③若的周长为,则,
如图所示,连接,过点分别作于点,作于点,
∵是的角平分线,,,
∴平分,,且,
∵,
∴,故结论③错误;
结论④若,则,
如图所示,连接,过点分别作于点,作于点,
∵,,且,∴,
如图所示,过点作于点,
∴,,∴,且,
∴,同理,,如图所示,
由结论②正确可知,,,且∴,
∴,∴,∴,故结论④正确;
综上所述,正确的有①②④,个,故选:.
【点睛】本题主要考查三角形的综合知识,掌握角的和差计算方法,角平分线的性质,三角形全等的判定和性质,角平分线交的性质,线段之间比例的计算方法等知识的综合是解题的关键.
6.(2023春·山东·七年级专题练习)如图,中,与的平分线交于点,过点作交于点,交于点,那么下列结论:
①和都是等腰三角形;②;③;④若,则.
其中正确的有( )个
A.1B.2C.3D.4
【答案】C
【分析】根据等腰三角形的判断与性质和平行线的性质及三角形三边的关系即可求解.
【详解】解:①∵BF是∠ABC的角平分线,CF是∠ACB的角平分线,∴∠ABF=∠CBF,∠ACF=∠BCF,
∵DE∥BC,∴∠CBF=∠BFD,∠BCF=∠EFC(两直线平行,内错角相等),
∴∠ABF=∠BFD,∠ACF=∠EFC,∴DB=DF,EF=EC,
∴△BDF和△CEF都是等腰三角形,∴①选项正确,符合题意;
②∵DE=DF+FE,∴DB=DF,EF=EC,∴DE=DB+CE,∴②选项正确,符合题意;
③根据题意不能得出BF>CF,∴④选项不正确,不符合题意;
④∵若∠A=80°,∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵∠ABF=∠CBF,∠ACF=∠BCF,∴∠CBF+∠BCF=×100°=50°,
∴∠BFC=180°-∠CBF-∠BCF=180°-50°=130°,∴④选项正确,符合题意;故①②④正确.故选C
【点睛】等腰三角形的判断与性质和平行线的性质及三角形三边的关系,解题关键是逐个判断选项即可得出正确答案.
7.(2023·广东·八年级期中)如图,已知,平分,,则( )
A.105°B.120°C.130°D.150°
【答案】B
【分析】本题主要利用邻补角互补,平行线性质及角平分线的性质进行做题.
【详解】∵∠CDE=150°,∴∠CDB=180−∠CDE=30°,又∵AB∥CD,∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,∴∠ABC=60°,∴∠C=180°−60°=120°.故选B.
【点睛】本题主要考查了平行线的性质,两直线平行,内错角相等,同旁内角互补.
8.(2023秋·四川南充·八年级校考期末)如图,内角和外角的平分线交于点,交于点,过点作交于点,交于点,连接,有以下结论;①;②;③若,则;④;⑤.其中正确的结论有( )
A.1个B.2个C.3个D.4个
【答案】C
【分析】①根据角相等推出线段相等,再将线段进行转化,即可证明;
②与不能得出全等的结论,无法证明;
③若,无法推出;④利用三角形面积的公式即可证明;
⑤通过设未知数找到等量关系,从而证明.
【详解】①∵∴,
∵内角和外角的平分线交于点
∴,∴,
∴,∴∴,故①正确.
②与只有两个角是相等的,能得出相似,但不含相等的边,所以不能得出全等的结论,不能推出,故②错误
③若,则,则,无法推出,故③错误
④的面积为乘以点到线段的距离乘以
的面积为乘以点到线段的距离乘以
点到线段的距离与点到线段的距离相等∴,故④正确
⑤过点E作于N,于D,于M,如图,
∵平分,∴
∵平分,∴∴,∴平分,
设,,,
则,,
∵,∴,∴∘,
∵,∴,∴,
即,故⑤正确;故选C
【点睛】本题考查平行线的性质,角平分线的定义,角平分线的性质与判定,等腰三角形的判定,三角形内角和定理,三角形外角的性质等多个知识点,解题的关键是灵活运用相关的定理进行求解.
9.(2023春·全国·七年级专题练习)如图,在中,已知和的平分线相交于点F,过点F作,交于D,交于E,若,则的周长为( )
A.6B.8C.10D.12
【答案】B
【分析】根据角平分线的定义得到,,平行线的性质得到,,等量代换得到,,根据等腰三角形的判定定理得到,,即可得到结论.
【详解】解:∵和的平分线相交于点F,∴,,
∵,∴,,
∴,,∴,,∵,
∴的周长为:.故选:B.
【点睛】本题考查了等腰三角形的判定,角平分线的定义,平行线的性质,证明,是解本题的关键.
10.(2022秋·江苏宿迁·八年级校考期末)如图,在中,,垂足为D,平分,交于点E,交于点F.若,则的长为( )
A.B.3C.D.
【答案】A
【分析】根据三角形的内角和定理得出,根据角平分线和对顶角相等得出,即可得出,再利用勾股定理得出的长,即可得出答案.
【详解】解:过点F作于点G,
∵,∴,∴,
∵平分,∴,∴,∴,
∵平分,,∴,
∴,∴,∴,
∵,∴,∴设,则,
则,解得:,即的长为.故选:A.
【点睛】本题考查了直角三角形性质、等腰三角形的性质和判定,三角形的内角和定理以及相似三角形的判定与性质等知识,关键是推出.
11.(2023春·四川达州·八年级校考阶段练习)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,则下列结论成立的是( )
A.EC=EFB.FE=FCC.CE=CFD.CE=CF=EF
【答案】C
【分析】求出∠CAF=∠BAF,∠B=∠ACD,根据三角形外角性质得出∠CEF=∠CFE,即可得出答案;
【详解】∵在Rt△ABC中,∠ACB=90°,CD⊥AB,∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,∴∠ACD=∠B,
∵AF平分∠CAB,∴∠CAE=∠BAF,∴∠ACD+∠CAE=∠B+∠BAF,
∴∠CEF=∠CFE,∴CE=CF.故选C.
【点睛】本题考查了直角三角形的性质,等腰三角形的判定,正确的识别图形是解题的关键.
12.(2023·成都市·八年级期中)如图,△ABC中,BD是 ∠ ABC的角平分线,DE ∥ BC,交AB 于 E,∠A=60º, ∠BDC=95º,则∠BED的度数是( )
A.35°B.70°C.110°D.130°
【答案】C
【分析】由三角形的外角性质得出∠ABD=35°,由角平分线的定义求出∠ABC=2∠ABD=70°,再由平行线的性质得∠BED+∠ABC=180°,即可得出结果.
【详解】∵∠BDC=∠A+∠ABD,∴∠ABD=95°−60°=35°,
∵BD是∠ABC的角平分线,∴∠ABC=2∠ABD=70°,
∵DE∥BC,∴∠BED+∠ABC=180°,∴∠BED=180°−70°=110°.故选C.
【点睛】本题主要考查三角形的外角性质,平行线的性质以及角平分线的定义,掌握三角形的外角的性质定理,是解题的关键.
13.(2023春·陕西咸阳·八年级咸阳市秦都中学校考阶段练习)如图,在中,,点为的边上一点,点分别在边上,连接,若,则的度数为 .
【答案】
【分析】根据角平分线的判定与性质可知,最后利用三角形的内角和定理即可解答.
【详解】解:过点作,垂足为,过点作,垂足为,
∵,,∴,
∵,∴,∴是的角平分线,∴,
∵,,∴,
∴,∴,故答案为.
【点睛】本题考查角平分线的判定与性质,三角形的内角和定理,掌握角平分线的判定与性质是解题关键.
14.(2023秋·安徽滁州·八年级统考期末)中,D是边上的点(不与点B,C重合),连接.
(1)如图1,当平分时,若,,则 ;
(2)如图2,平分,延长到E,使得,连接,如果,,,则 .
【答案】 / 9
【分析】(1)过作于E,于,根据角平分线性质得到,再根据三角形面积公式即可得到答案;
(2)根据可得到,再根据,和(1)的结论得到,即可求出的面积.
【详解】解:(1)如图1,过D作于E,于F,
是的角平分线,,
,,,故答案为:;
(2),∴,,,平分,
由(1)可知:,,
,故答案为:9.
【点睛】本题考查了角平分线性质和三角形的面积公式,灵活运用(1)(2)得出的结论是解题关键.
15.(2022秋·天津·八年级校考期中)如图,在中,是的平分线,延长至E,使,若,的面积为9,则的面积是 .
【答案】
【分析】由角平分线的性质可得,由三角形的面积关系可求解.
【详解】解:如图,过点作,交的延长线于,于,
∵的面积为9,∴,
∵是的平分线,,∴,
∵,∴,∴,∴,故答案为:.
【点睛】本题考查了角平分线的性质,三角形的面积公式,添加恰当辅助线是解题的关键.
16.(2022秋·湖北荆门·八年级统考期末)如图,在中,于点D,G是延长线上一点,平分,且,E是上一点,连接并延长交于点F.
(1)求证:;(2)猜想并证明:当E在何处时,.
【答案】(1)见解析(2)E是的中点,理由见解析
【分析】(1)根据角平分线的性质和平行线的性质证明即可;
(2)根据题意证明,即可推出.
【详解】(1)证明:∵平分,∴,
∵,∴,,
∴,∴;
(2)解:∵,,∴,
由(1)得,,∵,
当E是中点时,,∴,
∴,∴;
【点睛】本题考查几何证明,涉及到平行线的性质、角平分线的性质等,灵活运用所学知识是关键.
17.(2023·浙江八年级课时练习)如图,已知、的平分线相交于点,过点且.
(1)若,,求的度数;
(2)若,,求、的度数.
【答案】(1)125° (2)60°;40°
【分析】(1)由角平分线的定义可求得∠OBC=25°,∠OCB=30°,再利用三角形的内角和定理求解即可;(2)由已知条件易求∠1,∠2的度数,根据平行线的性质即可得∠OBC,∠OCB的度数,利用角平分线的定义可求解;
【详解】解:(1)∵和的平分线与相交于点,
∴,,
又,,∴,,
∴;
(2)∵,∴,
∵,∴,,
∵,∴,,
∵和的平分线与相交于点,∴,.
【点睛】本题主要考查角平分线的定义,三角形的内角和定理,平行线的性质,等腰三角形的性质等知识点的综合运用.
18.(2023广东江门八年级月考)(1)如图1,已知,在中,,平分,平分,过点作,分别交、于、两点,则图中共有________个等腰三角形:与、之间的数量关系是________,的周长是________.
(2)如图2,若将(1)中“中,”改为“若为不等边三角形,,”其余条件不变,则图中共有________个等腰三角形;与、之间的数量关系是什么?证明你的结论,并求出的周长.
(3)已知:如图3,在外,,且平分,平分的外角,过点作,分别交、于、两点,则与、之间又有何数量关系呢?写出结论并证明.
【答案】(1)5,,20(2)2,,证明见详解,18
(3),证明见详解
【分析】(1)根据角平分线的定义可得,再根据平行线的性质,“两直线平行,同位角相等”、“两直线平行,内错角相等”可知,
,即可求出,,根据“等角对等边”可知,即可确定等腰三角形的数量,与、之间的数量关系以及的周长; (2)若为不等边三角形,根据角平分线的定义可知,再结合平线性的性质“两直线平行,内错角相等”可知,即可推导,然后根据“等角对等边”即可证明,然后解答即可;
(3)根据角平分线的定义可知,再结合平线性的性质“两直线平行,内错角相等”可知,即可推导,然后根据“等角对等边”即可证明,即可证明与、之间的数量关系.
【详解】解:(1)∵,∴,
∵平分,平分,∴,∴,∴,
∵,∴,,
∴,,∴,
∴等腰三角形有,共计5个,∴,即,
∴的周长,
故答案为:5,,20;
(2)若为不等边三角形,
∵平分,平分,∴,
∵,∴,∴,
∴,∴等腰三角形有,共计2个,故答案为:2;
∵,∴,即;
∴的周长;
(3)与、之间的数量关系为:,
证明:∵平分,平分,∴,
∵,∴,∴,
∴,∴,即与、之间的数量关系为.
【点睛】本题主要考查了等腰三角形的判定与性质、平行线的性质、角平分线的定义等知识,熟练掌握等腰三角形的判定与性质是解题关键.
19.(2023·吉林·八年级校考期末)【教材呈现】如图是华师版八年级上册数学教材第96页的部分内容.
【定理证明】结合图①,“角平分线的性质定理”证明过程中.运用了与全等,全等最直接的依据是
【定理感知】如果教材中的已知条件不变,如图①,当,时,则面积为 .
【定理应用】如图②,在中,平分交于点D.求证:
【拓展应用】如图③,在中,,,,将先沿的平分线折叠,再剪掉重叠部分(即四边形),再将余下部分沿的平分线折叠,再剪掉重叠部分,直接写出剩余的的面积为 .
【答案】[定理证明]AAS ;[定理感知]9;[定理应用]见解析;[拓展应用]
【分析】[定理证明] 利用AAS证明全等即可;
[定理感知] 由,可得,即可求解;
[定理应用] 过点作,交的延长线于,通过证明,可得,可得结论;[拓展应用] 利用(2)的结论可求,,即可求解.
【详解】解:[定理证明] 平分,,
又,,;
[定理感知],,的面积;
[定理应用]如图②,过点作,交的延长线于,
平分,,
,,,,
,,,;
[拓展应用],,,,
将先沿的平分线折叠,,,,,
,由(2)可得,,,
,同理可求:,,
△的面积.故答案为:.
【点睛】本题是相似形综合题,考查了相似三角形的判定和性质,勾股定理,全等三角形的判定和性质等知识,灵活运用这些性质解决问题是本题的关键.
20.(2022秋·福建厦门·八年级厦门市湖里中学校考期中)如图,为的角平分线.
(1)如图1,若于点,交于点,,.则________;
(2)如图2,若,,的面积是10,求的面积;
(3)如图3,若,,,请直接写出的长(用含,的式子表示)
【答案】(1)2;(2)24;(3)
【分析】(1)利用ASA证明△AEF≌△ACF,得AE=AC=5,得出答案;
(2)作DE⊥AB交于点E,DF⊥AC交于点F,根据角平分线的性质得出DE=DF,根据的面积求出DF,再求△ABD的面积,最后求出的面积;(3)在AB上取AN=AC,可得CD=DN=m﹣n,根据△ABD和△ACD的高相等,面积比等于底之比可求出BD的长.
【详解】解:(1)∵AD是△ABC的平分线,∴∠BAD=∠CAD,
∵CE⊥AD,∴∠CFA=∠EFA,
在△AEF和△ACF中,∴△AEF≌△ACF(ASA),
∴AE=AC=5,∴BE=AB﹣AC=7﹣5=2,故答案为:2;
(2)如图,作DE⊥AB交于点E,DF⊥AC交于点F
∵的面积是10,AC=5,∴DF=2×10÷5=4,∵为的角平分线,∴DE=DF=4,
∴=,∴.
(3)如图,在AB上取AN=AC,
∵AD是△ABC的平分线,∴∠NAD=CAD,
在△ADN与△ADC中,
∴△ADN≌△ADC(SAS),∴∠AND=∠C,DN=CD,
∵∠C=2∠B,∴∠AND=2∠B,∴∠B=∠BDN,
∴BN=DN=AB﹣AC=m﹣n,∴CD=DN=m﹣n,
根据△ABD和△ACD的高相等,面积比等于底之比可得:
,∴,∴BD=,故答案为:.
【点睛】本题主要考查了全等三角形的判定与性质,角平分线的定义,三角形的面积等知识,利用角的轴对称性构造全等三角形是解题的关键.
人教版八年级数学上册专题08三角形中的特殊模型-双角平分线模型(原卷版+解析): 这是一份人教版八年级数学上册专题08三角形中的特殊模型-双角平分线模型(原卷版+解析),共38页。试卷主要包含了双角平分线模型等内容,欢迎下载使用。
中考数学专题练习08 三角形中的重要模型-平分平行(平分射影)构等腰、角平分线第二定理模型: 这是一份中考数学专题练习08 三角形中的重要模型-平分平行(平分射影)构等腰、角平分线第二定理模型,文件包含中考数学08三角形中的重要模型-平分平行平分射影构等腰角平分线第二定理模型教师版专题训练docx、中考数学08三角形中的重要模型-平分平行平分射影构等腰角平分线第二定理模型学生版专题训练docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
人教版八年级数学下学期题型模型培优专题练专题07锐角平分线模型-原卷版+解析: 这是一份人教版八年级数学下学期题型模型培优专题练专题07锐角平分线模型-原卷版+解析,共23页。












