2023-2024学年湖南省湘潭市岳塘区四校联考九年级（下）期中数学试卷（含解析）

这是一份2023-2024学年湖南省湘潭市岳塘区四校联考九年级（下）期中数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
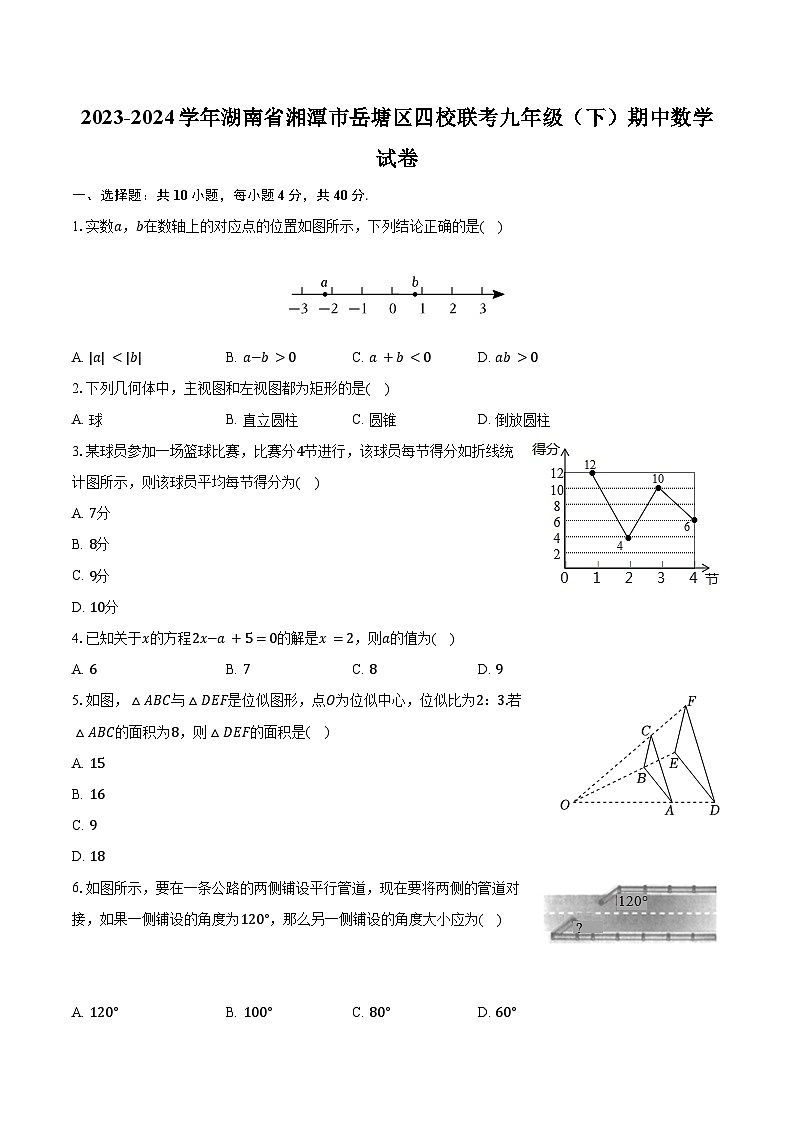
1.实数a，b在数轴上的对应点的位置如图所示，下列结论正确的是( )
A. |a|0C. a+b0
2.下列几何体中，主视图和左视图都为矩形的是( )
A. 球B. 直立圆柱C. 圆锥D. 倒放圆柱
3.某球员参加一场篮球比赛，比赛分4节进行，该球员每节得分如折线统计图所示，则该球员平均每节得分为( )
A. 7分
B. 8分
C. 9分
D. 10分
4.已知关于x的方程2x−a+5=0的解是x=2，则a的值为( )
A. 6B. 7C. 8D. 9
5.如图，△ABC与△DEF是位似图形，点O为位似中心，位似比为2：3.若△ABC的面积为8，则△DEF的面积是( )
A. 15
B. 16
C. 9
D. 18
6.如图所示，要在一条公路的两侧铺设平行管道，现在要将两侧的管道对接，如果一侧铺设的角度为120°，那么另一侧铺设的角度大小应为( )
A. 120°B. 100°C. 80°D. 60°
7.若点(−2,3)在反比例函数y=kx(k≠0)图象上，则该函数图象一定经过点( )
A. (3,2)B. (−3,2)C. (−3,−2)D. (−2,−3)
8.对于两个不相等的实数a、b，我们规定符号Max{a,b}表示a、b中的较大值，如：Max{2,4}=4，按照这个规定，方程Max{x,−x}=2x+1x的解为( )
A. 1− 2B. 2− 2
C. 1+ 2或1− 2D. 1+ 2或−1
9.如图，四边形ABCD内接于⊙O，AB=AD，∠BCD=120°，E、F分别为BC、CD上一点，∠EAF=30°，EF=3，DF=1.则BE的长为( )
A. 1
B. 2
C. 3
D. 4
10.已知二次函数y=ax2+bx+c，其中y与x的部分对应值如表：
下列结论正确的是( )
A. abc0
C. 若x3时，y>0
D. 方程ax2+bx+c=5的解为x1=−2，x2=3
二、填空题：本题共6小题，每小题4分，共24分。
11.分解因式：2x2y+4y= ______．
12.一只不透明的袋中，装有3枚白色棋子和n枚黑色棋子，除颜色外其余均相同.若小明从中随机摸出一枚棋子，多次实验后发现摸到黑色棋子的频率稳定在80%，则n的值可能是______．
13.在Rt△ABC中，∠C=90°，AB=4，BC=3，则sinA的值是______．
14.若关于x的一元一次不等式组x−22无解，则m的取值范围为______．
15.如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E.若∠CBF=18°，则∠AED等于______度．
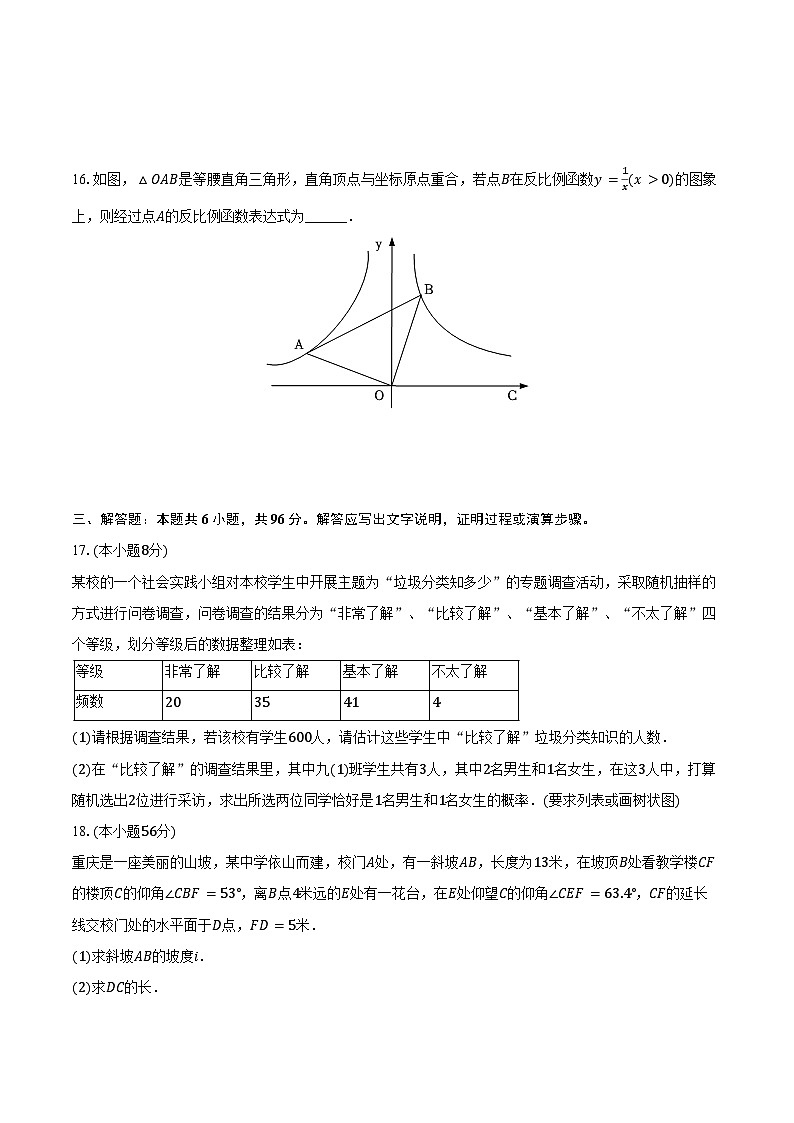
16.如图，△OAB是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数y=1x(x>0)的图象上，则经过点A的反比例函数表达式为______．
三、解答题：本题共6小题，共96分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如表：
(1)请根据调查结果，若该校有学生600人，请估计这些学生中“比较了解”垃圾分类知识的人数．
(2)在“比较了解”的调查结果里，其中九(1)班学生共有3人，其中2名男生和1名女生，在这3人中，打算随机选出2位进行采访，求出所选两位同学恰好是1名男生和1名女生的概率．(要求列表或画树状图)
18.(本小题56分)
重庆是一座美丽的山坡，某中学依山而建，校门A处，有一斜坡AB，长度为13米，在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°，离B点4米远的E处有一花台，在E处仰望C的仰角∠CEF=63.4°，CF的延长线交校门处的水平面于D点，FD=5米．
(1)求斜坡AB的坡度i．
(2)求DC的长．
(参考数据：tan53°≈43，tan63.4°≈2)
19.(本小题8分)
某学校建立了劳动基地，计划在基地上种植甲、乙两种树苗.已知甲种树苗的单价比乙种树苗的单价多10元；3棵甲种树苗与4棵乙种树苗的总价相等．
(1)求甲、乙两种树苗的单价分别为多少元？
(2)若购买甲、乙两种树苗共500棵，且甲种树苗的数量不少于乙种树苗的两倍.请为采购组设计最省钱的方案，并求出此时的总费用？
20.(本小题8分)
如图，点A，F，C，D在同一条直线上，点B，E分别在直线AD两侧，且AB=DE，∠A=∠D，AC=DF．
(1)求证：四边形BCEF是平行四边形，
(2)若∠ABC=90°，EF=3，AB=4，当CD为何值时，四边形BCEF是菱形．
21.(本小题8分)
已知：如图，AB是圆O的直径，CD是圆O的弦，AB⊥CD，E为垂足，AE=CD=8，F是CD延长线上一点，连接AF交圆O于G，连接AD、DG．
(1)求圆O的半径；
(2)求证：△ADG∽△AFD；
(3)当点G是弧AD的中点时，求△ADG得面积与△AFD的面积比．
22.(本小题8分)
抛物线y=ax2+bx+3过点A(−1,0)，点B(3,0)，顶点为C，与y轴相交于点D，点P是该抛物线上一动点，设点P的横坐标为m(1|b|，A选项错误，该选项不符合题意；
a−b