2022-2023学年福建省泉州七中高二（下）期末数学试卷

这是一份2022-2023学年福建省泉州七中高二（下）期末数学试卷，共21页。试卷主要包含了单选题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．（5分）设全集U＝{0，1，2，4，6，8}，集合M＝{0，4，6}，N＝{0，1，6}，则M∪∁UN＝（ ）
A．{0，2，4，6，8}B．{0，1，4，6，8}C．{1，2，4，6，8}D．U
2．（5分）若复数z＝3﹣4i，则z|z|=（ ）
A．35+45iB．35-45iC．-35+45iD．-35-45i
3．（5分）已知函数f(x)=(x+1)5，x＞1x2+2，x≤1，，则当0＜x＜1时，f（f（x））的展开式中x4的系数为（ ）
A．﹣270B．﹣216C．216D．270
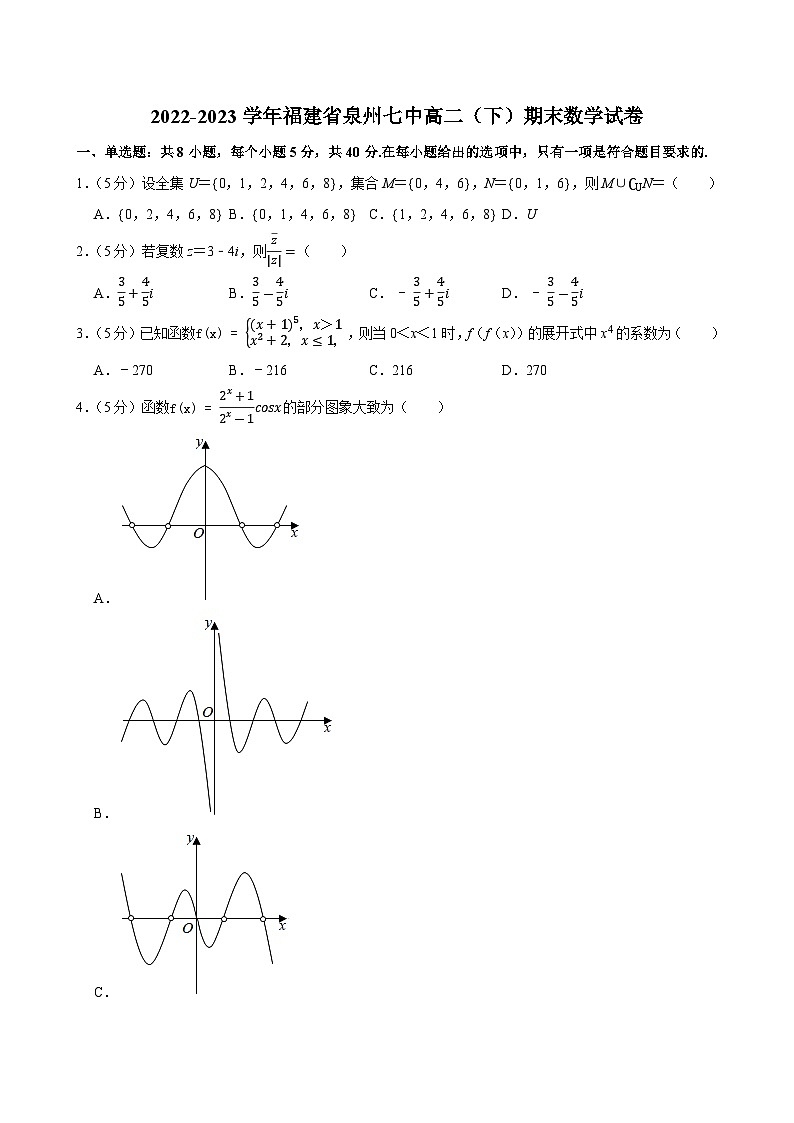
4．（5分）函数f(x)=2x+12x-1csx的部分图象大致为（ ）
A．
B．
C．
D．
5．（5分）某高校有智能餐厅A、人工餐厅B，甲第一天随机地选择一餐厅用餐，如果第一天去A餐厅，那么第二天去A餐厅的概率为0.6；如果第一天去B餐厅，那么第二天去A餐厅的概率为0.8．则甲第二天去A餐厅用餐的概率为（ ）
A．0.75B．0.7C．0.56D．0.38
6．（5分）已知双曲线C：x2a2-y2b2=1（a＞0，b＞0）的离心率为5，C的一条渐近线与圆（x﹣2）2+（y﹣3）2＝1交于A，B两点，则|AB|＝（ ）
A．55B．255C．355D．455
7．（5分）已知正实数a，b满足a+1b=2，则2ab+1a的最小值是（ ）
A．52B．3C．92D．22+1
8．（5分）对于定义在区间D上的函数f（x），若满足：∀x1，x2∈D且x1＜x2，都有f（x1）≤f（x2），则称函数f（x）为区间D上的“非减函数”，若f（x）为区间[0，2]上的“非减函数”，且f（2）＝2，f（x）+f（2﹣x）＝2，又当x∈[32，2]时，f（x）≤2（x﹣1）恒成立，下列命题中正确的有（ ）
A．f（1）＝0B．∃x0∈[32，2]，f(x0)＜1
C．∃x0∈[1，32]，f(x0)＞1D．∀x∈[0，1]，f（f（x））∈[0，1]
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
（多选）9．（5分）已知5个成对数据（x，y）的散点图如下，若去掉点D（4，3），则下列说法正确的是（ ）
A．变量x与变量y呈负相关
B．变量x与变量y的相关性变强
C．样本相关系数r变小
D．样本相关系数r变大
（多选）10．（5分）已知实数a，b，c满足2a＝lg2b=1c，则下列关系式中可能成立的是（ ）
A．b＝c＞aB．c＝a＞bC．b＞c＞aD．c＞b＞a
（多选）11．（5分）已知在正方体ABCD﹣A1B1C1D1中，点E，F分别为棱AB，BC上的中点，过E，F的平面α与底面ABCD所成的锐二面角为60°，则正方体被平面α所截的截面形状可能为（ ）
A．三角形B．四边形C．五边形D．六边形
（多选）12．（5分）已知定义在R上的函数f(x)，∀x，y∈R，f(x)f(y)=f(x+y)+2f(x-y)3，且f（x）≠0，则下述结论中正确的是（ ）
A．f（0）＝1
B．若f（1）＝1，则f（2024）＝2024
C．f（x）是偶函数
D．∃x∈R，f（x）＝﹣2
三、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.
13．（5分）已知向量a→=(1，2)，b→=(3，x)，a→与a→+b→共线，则|a→-b→|= ．
14．（5分）某工厂生产一批零件（单位：cm），其尺寸ξ服从正态分布N（μ，σ2），且P（ξ≤14）＝0.1，P（ξ＜18）＝0.9，则μ＝ ．
15．（5分）已知随机事件A，B，P（A）=13，P（B）=14，P（A|B）=34，则P(B|A)= ．
16．（5分）已知函数f（x）定义域为（0，+∞），f（1）＝e，对任意的x1，x2∈（0，+∞），当x2＞x1时，有f(x1)-f(x2)x1x2＞ex2x1-ex1x2(e是自然对数的底）．若f（lna）＞2e﹣alna，则实数a的取值范围是 ．
四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17．（10分）已知函数f（x）＝ax﹣a﹣x（a＞0，且a≠1），且f(1)=32．
（1）求a；
（2）f（2t）+f（t﹣1）＜0，求t的取值范围．
18．（12分）为普及空间站相关知识，某部门组织了空间站模拟编程闯关活动，它是由太空发射、自定义漫游、全尺寸太阳能、空间运输等10个相互独立的程序题目组成．规则是：编写程序能够正常运行即为程序正确．每位参赛者从10个不同的题目中随机选择3个进行编程，全部结束后提交评委测试，若其中2个及以上程序正确即为闯关成功．现已知10个程序中，甲只能正确完成其中6个，乙正确完成每个程序的概率为0.6，每位选手每次编程都互不影响．
（1）求乙闯关成功的概率；
（2）求甲编写程序正确的个数X的分布列和期望，并判断甲和乙谁闯关成功的可能性更大．
19．（12分）已知数列{an}满足an+an+2＝2an+1，n∈N*且a1＝1，a2＝3．
（1）求数列{an}的通项公式；
（2）若数列{bn}的前n项和为Sn，b1＝1，且满足3Sn＝bn+1﹣1，记cn=1an(lg2bn+3)，求数列{cn}的前n项和Tn．
20．（12分）已知函数f（x）＝x2•ex．
（Ⅰ）求f（x）的极值；
（Ⅱ）若函数y＝f（x）﹣ax在定义域内有三个零点，求实数a的取值范围．
21．（12分）受疫情影响，某校实行线上教学，为了监控学生的学习情况，每周进行一次线上测评，连续测评5周，得到均分数据见图．
（1）请你根据数据利用相关系数判定均分y与线上教学周数x是否具有显著相关关系，若有，求出线性回归方程，若没有，请说明理由；
（2）为了对比研究，该校和其水平相当的线下教学的联谊校进行同步测评，从两校分别随机抽取100名同学成绩进行优秀学生数统计见上表，试依据α＝0.100的独立性检验，分析优秀学生数与线上学习是否有关联？
附：相关系数：r=i=1n(xi-x)(yi-y)i=1n (xi-x)2i=1n (yi-y)2
回归系数：b̂=i=1n xiyi-nxyi=1n xi2-n(x)2=i=1n(xi-x)(yi-y)i=1n (xi-x)2，â=y-b̂xχ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)
临界值表：
22．（12分）已知圆O：x2+y2＝4，点F（1，0），以线段EF为直径的圆内切于圆O，点E的集合记为曲线C
（1）求曲线C的方程；
（2）若A，B是曲线C上关于坐标原点O对称的两点，点D（4，0），连结DA并延长交曲线C于点M，连结DB交曲线C于点N．设△DMN，△DAB的面积分别为S1，S2，若S1S2=37，求线段OA的长．
2022-2023学年福建省泉州七中高二（下）期末数学试卷
参考答案与试题解析
一、单选题：共8小题，每个小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.
1．（5分）设全集U＝{0，1，2，4，6，8}，集合M＝{0，4，6}，N＝{0，1，6}，则M∪∁UN＝（ ）
A．{0，2，4，6，8}B．{0，1，4，6，8}C．{1，2，4，6，8}D．U
【解答】解：由于∁UN＝{2，4，8}，
所以M∪∁UN＝{0，2，4，6，8}．
故选：A．
2．（5分）若复数z＝3﹣4i，则z|z|=（ ）
A．35+45iB．35-45iC．-35+45iD．-35-45i
【解答】解：z＝3﹣4i，
则z=3+4i，|z|=32+(-4)2=5，
故z|z|=3+4i5=35+45i．
故选：A．
3．（5分）已知函数f(x)=(x+1)5，x＞1x2+2，x≤1，，则当0＜x＜1时，f（f（x））的展开式中x4的系数为（ ）
A．﹣270B．﹣216C．216D．270
【解答】解：当0＜x＜1时，f（x）＝x2+2∈（2，3），
所以f（f（x））＝f（x2+2）＝（x2+3）5，
故f（f（x））的展开式即二项式（x2+3）5展开式，
其通项公式为Tr+1=C5r(x2)5-r3r=C5rx10-2r3r，
由10﹣2r＝4，得r＝3，
所以f（f（x））的展开式中x4的系数为C5333=270．
故选：D．
4．（5分）函数f(x)=2x+12x-1csx的部分图象大致为（ ）
A．
B．
C．
D．
【解答】解：函数的定义域为（﹣∞，0）∪（0，+∞），
因为f（﹣x）=2-x+12-x-1cs（﹣x）=1+2x1-2x•csx=-2x+12x-1csx＝﹣f（x），
所以f（x）为奇函数，排除选项A和D，
令f（x）＝0，则x=π2+kπ，k∈Z，
所以在y轴右侧，函数f（x）的第一个零点为x=π2，
不妨取x＝1，则f（1）=2+12-1•cs1＞0，即选项B正确，选项C错误．
故选：B．
5．（5分）某高校有智能餐厅A、人工餐厅B，甲第一天随机地选择一餐厅用餐，如果第一天去A餐厅，那么第二天去A餐厅的概率为0.6；如果第一天去B餐厅，那么第二天去A餐厅的概率为0.8．则甲第二天去A餐厅用餐的概率为（ ）
A．0.75B．0.7C．0.56D．0.38
【解答】解：设第一天去A餐厅为事件A1，第二天去A餐厅为事件A2，第一天去B餐厅为事件B1，
则P（A2）＝P（A2|A1）P（A1）+P（A2|B1）P（B1）＝0.6×0.5+0.8×0.5＝0.7．
故选：B．
6．（5分）已知双曲线C：x2a2-y2b2=1（a＞0，b＞0）的离心率为5，C的一条渐近线与圆（x﹣2）2+（y﹣3）2＝1交于A，B两点，则|AB|＝（ ）
A．55B．255C．355D．455
【解答】解：双曲线C：x2a2-y2b2=1（a＞0，b＞0）的离心率为5，
可得c=5a，所以b＝2a，
所以双曲线的渐近线方程为：y＝±2x，
一条渐近线与圆（x﹣2）2+（y﹣3）2＝1交于A，B两点，圆的圆心（2，3），半径为1，
圆的圆心到直线y＝2x的距离为：|4-3|1+4=15，
所以|AB|＝21-15=455．
故选：D．
7．（5分）已知正实数a，b满足a+1b=2，则2ab+1a的最小值是（ ）
A．52B．3C．92D．22+1
【解答】解：∵正实数a，b满足a+1b=2，∴ab+1＝2b，∴ab＝2b﹣1，
∴2ab+1a=4b+1a-2＝（4b+1a）（a+1b）×12-2＝（4ab+1ab+5）×12-2≥（24+5）×12-2=92-2=52，
当且仅当4ab=1ab，即a=23，b=34，时取等号，
∴2ab+1a的最小值是52，
故选：A．
8．（5分）对于定义在区间D上的函数f（x），若满足：∀x1，x2∈D且x1＜x2，都有f（x1）≤f（x2），则称函数f（x）为区间D上的“非减函数”，若f（x）为区间[0，2]上的“非减函数”，且f（2）＝2，f（x）+f（2﹣x）＝2，又当x∈[32，2]时，f（x）≤2（x﹣1）恒成立，下列命题中正确的有（ ）
A．f（1）＝0B．∃x0∈[32，2]，f(x0)＜1
C．∃x0∈[1，32]，f(x0)＞1D．∀x∈[0，1]，f（f（x））∈[0，1]
【解答】解：对于A，由f（x）+f（2﹣x）＝2，令x＝1，则有f（1）+f（1）＝2⇒f（1）＝1，故A不正确；
对于B，当x0=32时，f(32)≤2(32-1)=1，
又f(32)≥f(1)=1，
所以f(32)=1，
由题意x∈[32，2]，f(x)≥f(32)=1，故B不正确；
对于C中，因为f（1）＝1，f（32）＝1，
因为：∀x1，x2∈D且x1＜x2，都有∀x1，x2∈D且x1＜x2，
所以当1≤x≤32时，f（1）＝1，故C不正确；
对于D中，当x＝0时，f（0）+f（2）＝2⇒f（0）＝0，
又f（1）＝1，
所以0≤x≤1时，0≤f（x）≤1，
所以f（f（x））∈[0，1]，故D正确．
故选：D．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
（多选）9．（5分）已知5个成对数据（x，y）的散点图如下，若去掉点D（4，3），则下列说法正确的是（ ）
A．变量x与变量y呈负相关
B．变量x与变量y的相关性变强
C．样本相关系数r变小
D．样本相关系数r变大
【解答】解：由散点图可知，只有D（4，3）偏离直线最远，
当去掉点D（4，3）后，变量x与变量y的线性相关变强，且为负相关，
故选项A和选项B正确；
此时相关系数r变小，故选项C正确，选项D错误．
故选：ABC．
（多选）10．（5分）已知实数a，b，c满足2a＝lg2b=1c，则下列关系式中可能成立的是（ ）
A．b＝c＞aB．c＝a＞bC．b＞c＞aD．c＞b＞a
【解答】解：∵2a=lg2b=1c，令y1=2x，y2=lg2x，y3=1x，
记y1=2x与y3=1x交点的纵坐标为m，y2＝lg2x与y3=1x交点的纵坐标为t，
在同一坐标系中作出函数y1=2x，y2=lg2x，y3=1x的图象，
当y＝t时，A正确；
当y＝m时，B错误；
当t＜y＜m时，C正确；
当y＜t时，D正确．
故选：ACD．
（多选）11．（5分）已知在正方体ABCD﹣A1B1C1D1中，点E，F分别为棱AB，BC上的中点，过E，F的平面α与底面ABCD所成的锐二面角为60°，则正方体被平面α所截的截面形状可能为（ ）
A．三角形B．四边形C．五边形D．六边形
【解答】解：如图所示：
设正方体的棱长为4a，在BB1上取一点G使得平面EFG与平面ABCD所成的锐二面角为60°，
因为E，F分别为棱AB，BC的中点，
所以EG＝FG，
连接BD交EF于点N，连接AC，
所以EF⊥BN，且N为EF的中点，
BN=14BD，
所以GN⊥EF，
所以∠GNB为平面EFG与平面ABCD所成的锐二面角为60°，
所以GB＝tan60°•BN=3×14×42a=6a，
所以GBBB1=6a4a=64，
所以此时平面EFG为平面α，
所以平面α为三角形，故A正确；
在AA1和CC1上分别取点M和点H，使得AM＝CH，
取MH，AC的中点K，O，
则KO⊥平面ABCD，
又因为EF⊂平面ABCD，
所以KO⊥EF又NO⊥EF，
所以EF⊥平面KNO，
又因为KN⊂平面KNO，
所以∠KNO为平面MEFH与平面ABCD所成的锐二面角为60°，
所以KO＝tan60°•ON=3×14×42a=6a，
所以KOBB1=MAAA1=CHCC1=6a4a=64，
延长FH交B1C1于T，延长EM交B1A1于S，连接ST交A1D1于Q，交C1D1于P，
连接HP，MQ，则平面MEFHPQ为平面α，
所以平面α为六边形，故D正确．
故选：AD．
（多选）12．（5分）已知定义在R上的函数f(x)，∀x，y∈R，f(x)f(y)=f(x+y)+2f(x-y)3，且f（x）≠0，则下述结论中正确的是（ ）
A．f（0）＝1
B．若f（1）＝1，则f（2024）＝2024
C．f（x）是偶函数
D．∃x∈R，f（x）＝﹣2
【解答】解：令x＝0，y＝0，则f2(0)=f(0)+2f(0)3=f(0)，因为f（x）≠0，所以f（0）＝1，A正确；
令y＝x，则f2(x)=f(2x)+2f(0)3，所以f（2x）＝3f2（x）﹣2f（0）＝3f2（x）﹣2，
所以f（2x）﹣1＝3[f2（x）﹣1]＝3[f（x）﹣1]•[f（x）+1]，
若f（1）＝1，则f（2）＝1，f（4）＝1，f（8）＝1，⋯，f（2024）＝1，B错误；
令x＝0，则f(0)f(y)=f(y)+2f(-y)3，即3f（y）＝f（y）+2f（﹣y），
所以f（y）＝f（﹣y），f（x）是偶函数，C正确；
因为f（x）≠0，所以f（2x）＝3f2（x）﹣2＞﹣2，
所以∀x∈R，f（x）＞﹣2，D错误．
故选：AC．
三、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.
13．（5分）已知向量a→=(1，2)，b→=(3，x)，a→与a→+b→共线，则|a→-b→|= 25 ．
【解答】解：∵a→=（1，2），b→=（3，x），∴a→+b→=（4，2+x），
∵a→与a→+b→共线，
∴2+x＝8，∴x＝6，
∴b→=（3，6），∴a→-b→=（﹣2，﹣4），
则|a→-b→|=(-2)2+(-4)2=25，
故答案为：25．
14．（5分）某工厂生产一批零件（单位：cm），其尺寸ξ服从正态分布N（μ，σ2），且P（ξ≤14）＝0.1，P（ξ＜18）＝0.9，则μ＝ 16 ．
【解答】解：∵ξ～N（μ，σ2），P（ξ≤14）+P（ξ＜18）＝0.1+0.9＝1，
∴P（ξ≤14）＝1﹣P（ξ＜18）＝P（ξ≥18），
∴μ=14+182=16．
故答案为：16．
15．（5分）已知随机事件A，B，P（A）=13，P（B）=14，P（A|B）=34，则P(B|A)= 716 ．
【解答】解：依题意得P(A|B)=P(AB)P(B)=34，所以P(AB)=34P(B)=34×14=316，
故P(B|A)=P(AB)P(A)=31613=916，
所以P(B|A)=1-P(B|A)=716．
故答案为：716．
16．（5分）已知函数f（x）定义域为（0，+∞），f（1）＝e，对任意的x1，x2∈（0，+∞），当x2＞x1时，有f(x1)-f(x2)x1x2＞ex2x1-ex1x2(e是自然对数的底）．若f（lna）＞2e﹣alna，则实数a的取值范围是 （1，e） ．
【解答】解：由题意当 x 2＞ x 1时，有f(x1)-f(x2)x1x2＞ex2x1-ex1x2，即f（x1）﹣f（x2）＞x2ex2-x1ex1，
即f（x1）+x1ex1＞f（x2）+x2ex2，故令g（x）＝f（x）+xex，则当x2＞x1＞0时，g（x1）＞g（x2），
则g（x）在（0，+∞）上单调递减，
由于f（1）＝e，而f（lna）＞2e﹣alna，
即有f（lna）+alna＞f（1）+1×e1，即g（lna）＞g（1），
所以0＜lna＜1，∴1＜a＜e，
即实数 a 的取值范围是（1，e）．
故答案为：（1，e）．
四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17．（10分）已知函数f（x）＝ax﹣a﹣x（a＞0，且a≠1），且f(1)=32．
（1）求a；
（2）f（2t）+f（t﹣1）＜0，求t的取值范围．
【解答】解：（1）因为f(1)=32，
所以a-1a=32，即2a2﹣3a﹣2＝0，
所以a=-12，或a＝2．
又因为a＞0，且a≠1，
所以a＝2．
（2）由（1）得a＝2，所以f(x)=2x-12x，
因为y＝2x和y=-12x在R上是增函数，所以f（x）在R上是增函数，
又因为f(-x)=2-x-12-x=-(2x-12x)=-f(x)，所以f（x）为奇函数，
因为f（2t）+f（t﹣1）＜0，所以f（2t）＜﹣f（t﹣1）＝f（1﹣t），
所以2t＜1﹣t，所以t＜13，
即t的取值范围是（﹣∞，13）．
18．（12分）为普及空间站相关知识，某部门组织了空间站模拟编程闯关活动，它是由太空发射、自定义漫游、全尺寸太阳能、空间运输等10个相互独立的程序题目组成．规则是：编写程序能够正常运行即为程序正确．每位参赛者从10个不同的题目中随机选择3个进行编程，全部结束后提交评委测试，若其中2个及以上程序正确即为闯关成功．现已知10个程序中，甲只能正确完成其中6个，乙正确完成每个程序的概率为0.6，每位选手每次编程都互不影响．
（1）求乙闯关成功的概率；
（2）求甲编写程序正确的个数X的分布列和期望，并判断甲和乙谁闯关成功的可能性更大．
【解答】解：（1）根据题意，记事件A为“乙闯关成功”，乙正确完成每个程序的概率为0.6，
则P(A)=C32×0．62×(1-0.6)+(0.6)3=0.648；
（2）甲编写程序正确的个数X的可能取值为3，2，1，0，
P(X=0)=C43C103=130，
P(X=1)=C61⋅C42C103=310，
P(X=2)=C62C41C103=12，
P(X=3)=C63C103=16，
故甲编写程序正确的个数X的分布列为：
则甲编写程序正确的个数X的数学期望E(X)=0×130+1×310+2×12+3×16=95，
甲闯关成功的概率P=12+16=23＞0.648，
故甲比乙闯关成功的概率要大．
19．（12分）已知数列{an}满足an+an+2＝2an+1，n∈N*且a1＝1，a2＝3．
（1）求数列{an}的通项公式；
（2）若数列{bn}的前n项和为Sn，b1＝1，且满足3Sn＝bn+1﹣1，记cn=1an(lg2bn+3)，求数列{cn}的前n项和Tn．
【解答】解：（1）数列{an}满足an+an+2＝2an+1，
即为an+2﹣an+1＝an+1﹣an＝...＝a2﹣a1，
所以{an}是等差数列，且公差为a2﹣a1＝2，首项为1，
则an＝1+2（n﹣1）＝2n﹣1；
（2）当n＝1时，3b1＝3S1＝b2﹣1＝3，可得b2＝4；
当n≥2时，3Sn﹣1＝bn﹣1，又3Sn＝bn+1﹣1，
两式相减可得3bn＝bn+1﹣bn，
即bn+1＝4bn，
当n＝1时，上式也成立．
所以bn＝4n﹣1，
cn=1an(lg2bn+3)=1(2n-1)(lg24n-1+3)=1(2n-1)(2n+1)=12（12n-1-12n+1），
所以Tn=12（1-13+13-15+...+12n-1-12n+1）=12（1-12n+1）=n2n+1．
20．（12分）已知函数f（x）＝x2•ex．
（Ⅰ）求f（x）的极值；
（Ⅱ）若函数y＝f（x）﹣ax在定义域内有三个零点，求实数a的取值范围．
【解答】解：由题意可知函数f（x）的定义域为R．
（Ⅰ）因为f（x）＝x2•ex．
所以f′（x）＝ex（x2+2x），
由f′（x）＝0，得x1＝﹣2，x2＝0，
当x＜﹣2时，f′（x）＞0，函数单调递增，当﹣2＜x＜0时，f′（x）＜0，函数单调递减，当x＞0时，f′（x）＞0，函数单调递增，
因此，当x＝﹣2时，f（x）有极大值，并且极大值为f（﹣2）=4e2；
当x＝0时，f（x）有极小值，并且极小值为f（0）＝0．
（Ⅱ）因为y＝f（x）﹣ax＝x2•ex﹣ax，
所以x＝0为一个零点．
所以“函数y＝x2•ex﹣ax，在定义域内有三个零点”可以转化为“方程a＝xex有两个非零实根”．
令h（x）＝xex，则h′（x）＝（x+1）ex，
所以，当x＜﹣1时，h′（x）＜0，h（x）在（﹣∞，﹣1）上单调递减；
当x＞﹣1时，h′（x）＞0，h（x）在（﹣1，+∞）上单调递增；
当x＝﹣1时，h（x）有最小值h（﹣1）=-1e．
若方程a＝xex有两个非零实根，则h（﹣1）=-1e＜a，即a＞-1e．
若a≥0，方程a＝xex只有一个非零实根，
所以a＜0．
综上，-1e＜a＜0．
21．（12分）受疫情影响，某校实行线上教学，为了监控学生的学习情况，每周进行一次线上测评，连续测评5周，得到均分数据见图．
（1）请你根据数据利用相关系数判定均分y与线上教学周数x是否具有显著相关关系，若有，求出线性回归方程，若没有，请说明理由；
（2）为了对比研究，该校和其水平相当的线下教学的联谊校进行同步测评，从两校分别随机抽取100名同学成绩进行优秀学生数统计见上表，试依据α＝0.100的独立性检验，分析优秀学生数与线上学习是否有关联？
附：相关系数：r=i=1n(xi-x)(yi-y)i=1n (xi-x)2i=1n (yi-y)2
回归系数：b̂=i=1n xiyi-nxyi=1n xi2-n(x)2=i=1n(xi-x)(yi-y)i=1n (xi-x)2，â=y-b̂xχ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)
临界值表：
【解答】解：（1）x=1+2+3+4+55=3，
y=86+84+85+82+835=84，
i=15 (xi-x)(yi-y)=（﹣2）×2+（﹣1）×0+0×1+1×（﹣2）+2×（﹣1）＝﹣8，
i=15 (xi-x)2=10，i=15 (yi-y)2=10，
则r=i=15 (xi-x)(yi-y)i=15 (xi-x)2i=15 (yi-y)2=-810=-0.8∈[﹣1，﹣0.75]，
则均分y与线上教学周数x负相关很强；
b̂=i=15 (xi-x)(yi-y)i=15 (xi-x)2=-810=-0.8，â=y-b̂x=84-(-0.8)×3=86.4，
则线性回归方程为ŷ=-0.8x+86.4．
（2）零假设为H0：优秀数与线上学习相互独立，即优秀数与线上学习之间无关联．
χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)=200(46×44-56×54)2102×98×100×100=50002499≈2.001＜2.706．
依据小概率值α＝0.100的独立性检验，没有充分证据推断零假设H0不成立，
因此可以认为H0成立，即认为优秀数与线上学习之间无关联．
22．（12分）已知圆O：x2+y2＝4，点F（1，0），以线段EF为直径的圆内切于圆O，点E的集合记为曲线C
（1）求曲线C的方程；
（2）若A，B是曲线C上关于坐标原点O对称的两点，点D（4，0），连结DA并延长交曲线C于点M，连结DB交曲线C于点N．设△DMN，△DAB的面积分别为S1，S2，若S1S2=37，求线段OA的长．
【解答】解：（1）设EF的中点为P，切点为Q，连接O，P，Q，取F关于y轴的对称点F1，
则|FF1|＝2，连接EF1，
所以OP为△EF1F的中位线，即|EF1|＝2|OP|，
所以|EF|+|EF1|＝2|OP|+2|PF|＝2|OP|+2|PQ|＝2（|OP|+|PQ|）＝4＞|F1F|＝2，
所以点E的轨迹是以F1，F为焦点，长轴长为4的椭圆，其中a=2，c=1，b=3，
所以曲线C的方程为x24+y23=1．
（2）设A（x0，y0），则B（﹣x0，﹣y0），
根据题意设直线DA的方程为x＝my+4，即m=x0-4y0，
联立x=my+4x24+y23=1，得（3m2+4）y2+24my+36＝0，
Δ＝（24m）2﹣4×36（3m2+4）＝m2﹣4＞0，即m＞2或m＜﹣2，
yMyA=363m2+4=363(x0-4y0)2+4=36y023(x0-4)2+4y02，
因为yA＝y0，
所以yM=36y03(x0-4)2+4y02，
又因为点A在椭圆上，
所以4y02=12﹣3x02，代入上式可得yM=3y05-2x0，
同理可得yN=-3y05+2x0，
所以S1S2=12|DM||DN|sin∠MDN12|DB||DA|sin∠MDN=|DM||DA|•|DN||DB|=|yMyA|•|yNyB|=925-4x02=37，
解得x02=1，y02=94，
所以|OA|=x02+y02=132．
优秀数
非优秀数
合计
某校
46
54
100
联谊校
56
44
100
合计
102
98
200
α
0.100
0.050
0.010
0.001
xα
2.706
3.841
6.635
10.828
X
0
1
2
3
P
130
310
12
16
优秀数
非优秀数
合计
某校
46
54
100
联谊校
56
44
100
合计
102
98
200
α
0.100
0.050
0.010
0.001
xα
2.706
3.841
6.635
10.828