2022-2023学年湖南师大附中高一（下）期末数学试卷（含答案解析）

这是一份2022-2023学年湖南师大附中高一（下）期末数学试卷（含答案解析），共21页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．（5分）已知全集U＝{1，2，3，4，5}，A＝{1，2}，B＝{2，3，4}，则A∩（∁UB）＝（ ）
A．{1}B．{5}C．{1，5}D．{1，2}
2．（5分）已知复数（i是虚数单位），则（ ）
A．2﹣iB．2+iC．﹣2+iD．﹣2﹣i
3．（5分）如图，在平行四边形ABCD中，对角线AC与BD交于点O，且E为AO的中点，则（ ）
A．B．C．D．
4．（5分）某地区中小学生人数比例和近视情况分别如图甲和图乙所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法随机抽取2%的学生进行调查，其中被抽取的小学生有80人，则样本容量和该地区的初中生近视人数分别为（ ）
A．100，50B．100，1050C．200，50D．200，1050
5．（5分）下列说法不正确的是（ ）
A．若直线a∥平面α，则直线a与平面α内的任意一条直线都无公共点
B．若α∩β＝a，β∩γ＝b，且a∥b，则α∥γ
C．垂直于同一条直线的两个平面互相平行
D．垂直于同一个平面的两条直线互相平行
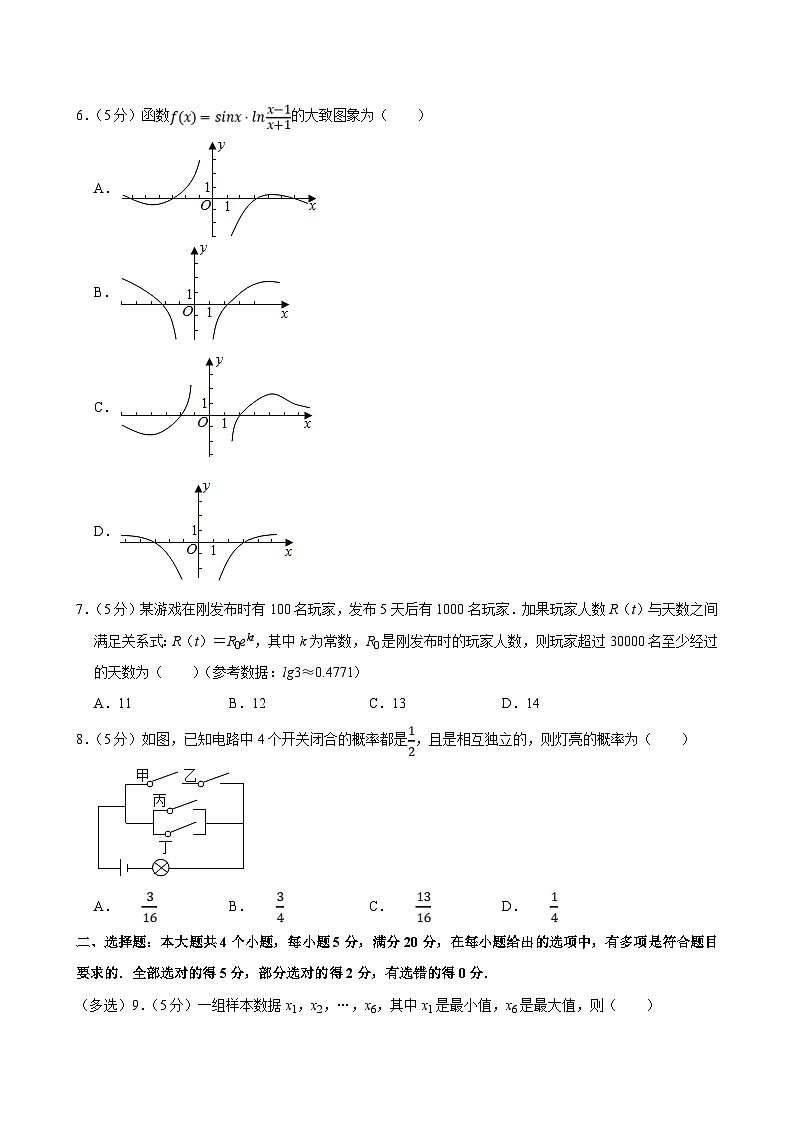
6．（5分）函数的大致图象为（ ）
A．
B．
C．
D．
7．（5分）某游戏在刚发布时有100名玩家，发布5天后有1000名玩家．加果玩家人数R（t）与天数之间满足关系式：R（t）＝R0ekt，其中k为常数，R0是刚发布时的玩家人数，则玩家超过30000名至少经过的天数为（ ）（参考数据：lg3≈0.4771）
A．11B．12C．13D．14
8．（5分）如图，已知电路中4个开关闭合的概率都是，且是相互独立的，则灯亮的概率为（ ）
A．B．C．D．
二、选择题：本大题共4个小题，每小题5分，满分20分，在每小题给出的选项中，有多项是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分．
（多选）9．（5分）一组样本数据x1，x2，…，x6，其中x1是最小值，x6是最大值，则（ ）
A．x2，x3，x4，x5的平均数等于x1，x2，…，x6的平均数
B．x2，x3，x4，x5的第60百分位数等于x1，x2，…，x6的第60百分位数
C．x2，x3，x4，x5的标准差小于x1，x2，…，x6的标准差
D．x2，x3，x4，x5的极差不大于x1，x2，…，x6的极差
（多选）10．（5分）已知ea＞eb，则下列不等式一定成立的有（ ）
A．B．πa﹣b＞1
C．a2023＞b2023D．lg（a﹣b）＞1
（多选）11．（5分）一个质地均匀的正四面体木块的四个面上分别标有数字1，2，3，4连续抛掷这个正四面体木块两次，并记录每次正四面体木块朝下的面上的数字，记事件A为“第一次向下的数字为2或3”，事件B为“两次向下的数字之和为奇数”，则下列结论正确的是（ ）
A．
B．事件A与事件B互斥
C．事件A与事件B相互独立
D．
（多选）12．（5分）如图，在边长为4的正方形ABCD中，点E是AB的中点，点F是BC的中点，点P是AD上的动点，将△ADE，△CDF分别沿DE，DF折起，使A，C两点重合于点G，则下列结论正确的是（ ）
A．BG⊥EF
B．G到平面DEF的距离为
C．若BG∥面EFP，则二面角D﹣EF﹣P的余弦值为
D．四面体G﹣DEF外接球表面积为24π
三、填空题：本大题共4个小题，每小题5分，共20分．
13．（5分）已知，则sin2θ＝ ．
14．（5分）以棱长为1的正方体各面的中心为顶点，构成一个正八面体，那么这个正八面体的表面积是 ．
15．（5分）一个袋子中有大小和质地相同的5个球，其中有3个红色球，2个白色球，从袋中不放回地依次随机摸出2个球，则第2次摸到红色球的概率为 ．
16．（5分）在△ABC中，（2m，m+5），（csα，sinα），（m∈R，α∈R），若对任意的实数t，恒成立，则BC边的最小值是 ．
三、解答题：本大题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤．
17．（10分）如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，侧面ADP是正三角形，侧面ADP⊥底面ABCD，M是DP的中点．
（1）求证：AM⊥平面CDP；
（2）求直线BP与底面ABCD所成角的正弦值．
18．（12分）已知在△ABC中，A+B＝2C，2sin（A﹣C）＝sinB．
（1）求sinA；
（2）设，求△ABC的面积．
19．（12分）已知向量，，记函数．
（1）求使函数f（x）≤0成立的x的取值集合；
（2）已知α，β均为锐角，，，求sin（2α﹣β）的值．
20．（12分）某地区为了解市民的心理健康状况，随机抽取了n位市民进行心理健康问卷调查，将所得评分百分制按国家制定的心理测评评价标准整理，得到频率分布直方图．已知调查评分在[70，80）中的市民有200人．
心理测评评价标准
（1）求n的值及频率分布直方图中t的值；
（2）该地区主管部门设定预案：若市民心理健康指数的平均值不低于0.75，则只需发放心理指导资料，否则需要举办心理健康大讲堂．根据调查数据，判断该市是否需要举办心理健康大讲堂，并说明理由．（每组的每个数据用该组区间的中点值代替，心理健康指数＝调查评分÷100）
（3）在抽取的心理等级为D的市民中，按照调查评分的分组，分为2层，通过分层随机抽样抽取3人进行心理疏导．据以往数据统计，经心理疏导后，调查评分在[40，50）的市民的心理等级转为B的概率为，调查评分在[50，60）的市民的心理等级转为B的概率为，假设经心理疏导后的等级转化情况相互独立，求在抽取的3人中，经心理疏导后恰有一人的心理等级转为B的概率；
21．（12分）如图，在棱长为3的正方体ABCD﹣A'B'C'D'中，M为AD的中点．
（1）求证：DB'∥平面BMA'；
（2）在体对角线DB'上是否存在动点Q，使得AQ⊥平面BMA'？若存在，求出DQ的长；若不存在，请说明理由．
22．（12分）设函数f（x）的定义域为D，对于区间I＝[a，b]（a＜b，I⊆D），若满足以下两条性质之一，则称I为f（x）的一个“Ω区间”．
性质1：对任意x∈I，有f（x）∈I；
性质2：对任意x∈I，有f（x）∉I．
（1）分别判断区间[1，2]是否为下列两函数的“Ω区间”（直接写出结论）；
①y＝3﹣x；②；
（2）若[0，m]（m＞0）是函数f（x）＝﹣x2+2x的“Ω区间”，求m的取值范围；
（3）已知定义在R上，且图象连续不断的函数f（x）满足：对任意a，b∈R，且a＜b，有f（a）﹣f（b）＞b﹣a．求证：f（x）存在“Ω区间”，且存在x0∈R，使得x0不属于f（x）的任意一个“Ω区间”．
2022-2023学年湖南师大附中高一（下）期末数学试卷
参考答案与试题解析
一、选择题：本大题共8个小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（5分）已知全集U＝{1，2，3，4，5}，A＝{1，2}，B＝{2，3，4}，则A∩（∁UB）＝（ ）
A．{1}B．{5}C．{1，5}D．{1，2}
【解答】解：由已知可得∁UB＝{1，5}，
所以A∩（∁UB）＝{1}，
故选：A．
2．（5分）已知复数（i是虚数单位），则（ ）
A．2﹣iB．2+iC．﹣2+iD．﹣2﹣i
【解答】解：2﹣i，
则2+i．
故选：C．
3．（5分）如图，在平行四边形ABCD中，对角线AC与BD交于点O，且E为AO的中点，则（ ）
A．B．C．D．
【解答】解：由题意可得：，
则．
故选：C．
4．（5分）某地区中小学生人数比例和近视情况分别如图甲和图乙所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法随机抽取2%的学生进行调查，其中被抽取的小学生有80人，则样本容量和该地区的初中生近视人数分别为（ ）
A．100，50B．100，1050C．200，50D．200，1050
【解答】解：由题意知，被抽取的小学生有80人，则样本容量为80÷40%＝200；
所以该地区的学生人数为200÷2%＝10000，
所以该地区初中生近视人数为10000×35%×30%＝1050．
故选：D．
5．（5分）下列说法不正确的是（ ）
A．若直线a∥平面α，则直线a与平面α内的任意一条直线都无公共点
B．若α∩β＝a，β∩γ＝b，且a∥b，则α∥γ
C．垂直于同一条直线的两个平面互相平行
D．垂直于同一个平面的两条直线互相平行
【解答】解：A项：直线与平面平行，即没有公共点，故直线与平面内任意一条直线都无公共点，A项正确；
B项：α和β有可能平行，有可能相交，B项错误；
C项：由直线和平面垂直的性质可知垂直于同一条直线的两个平面互相平行，C项正确；
D项，由直线和平面垂直的性质定理可知垂直于同一个平面的两条直线互相平行，D项正确．
故选：B．
6．（5分）函数的大致图象为（ ）
A．
B．
C．
D．
【解答】解：f（﹣x）＝﹣sinx•lnsinx•lnsinx•lnf（x），则函数f（x）是偶函数，图象关于y轴对称，
排除A，C，
f（3）＝sin3ln0，排除B，
故选：D．
7．（5分）某游戏在刚发布时有100名玩家，发布5天后有1000名玩家．加果玩家人数R（t）与天数之间满足关系式：R（t）＝R0ekt，其中k为常数，R0是刚发布时的玩家人数，则玩家超过30000名至少经过的天数为（ ）（参考数据：lg3≈0.4771）
A．11B．12C．13D．14
【解答】解：由题意得，
故，
又R（t）＞30000，即t＞5lg300＝5（lg3+2）≈12.3855＞12，
∴至少经过的天数为13．
故选：C．
8．（5分）如图，已知电路中4个开关闭合的概率都是，且是相互独立的，则灯亮的概率为（ ）
A．B．C．D．
【解答】解：由题意知，本题是一个相互独立事件同时发生的概率，
灯泡不亮包括四个开关都开，或下边的2个都开，上边的2个中有一个开，
这三种情况是互斥的，每一种情况中的事件是相互独立的，
∴灯泡不亮的概率是 ，
∵灯亮和灯不亮是两个对立事件，
∴灯亮的概率是1，
故选：C．
二、选择题：本大题共4个小题，每小题5分，满分20分，在每小题给出的选项中，有多项是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分．
（多选）9．（5分）一组样本数据x1，x2，…，x6，其中x1是最小值，x6是最大值，则（ ）
A．x2，x3，x4，x5的平均数等于x1，x2，…，x6的平均数
B．x2，x3，x4，x5的第60百分位数等于x1，x2，…，x6的第60百分位数
C．x2，x3，x4，x5的标准差小于x1，x2，…，x6的标准差
D．x2，x3，x4，x5的极差不大于x1，x2，…，x6的极差
【解答】解：因为在一组样本数据x1，x2，…，x6，其中x1是最小值，x6是最大值，
对于选项A：不妨令x2＝x3＝x4＝x5＝4，x1＝1，x6＝6，
此时40，故选项A错误；
对于选项B：不妨令x5≥x4≥x3≥x2，
因为4×0.6＝2.4，
所以x2，x3，x4，x5的第60百分位数为x4，
又x1为最小值，x6为最大值，且6×0.6＝3.6，
所以x1，x2，x3，x4，x5，x6的第60百分位数为x4，故选项B正确；
对于选项C：不妨令x1＝x2＝x3＝x4＝x5＝x6＝7，
此时x1，x2，…，x6的平均数7，
则标准差s10，
而x2，x3，x4，x5的平均数7，
则标准差s20，
因为s1＝s2，故选项C错误；
对于选项D：不妨设x2，x3，x4，x5中x2为最小值，x5为最大值，
此时x6﹣x1≥x5﹣x2，当且仅当x1＝x2，x5＝x6时等号成立，故选项D正确．
故选：BD．
（多选）10．（5分）已知ea＞eb，则下列不等式一定成立的有（ ）
A．B．πa﹣b＞1
C．a2023＞b2023D．lg（a﹣b）＞1
【解答】解：对于A，令a＝1，b＝﹣1，则，故选项A错误；
对于B，因为ea＞eb，所以a＞b，即a﹣b＞0，所以πa﹣b＞π0＝1，B正确；
对于C，由于a＞b且函数y＝x2023是增函数，所以a2023＞b2023，C正确；
对于D，令a＝1，b＝0，则lg（a﹣b）＝0＜1，D错误．
故选：BC．
（多选）11．（5分）一个质地均匀的正四面体木块的四个面上分别标有数字1，2，3，4连续抛掷这个正四面体木块两次，并记录每次正四面体木块朝下的面上的数字，记事件A为“第一次向下的数字为2或3”，事件B为“两次向下的数字之和为奇数”，则下列结论正确的是（ ）
A．
B．事件A与事件B互斥
C．事件A与事件B相互独立
D．
【解答】解：对于A，P（A），A错误；
对于B，实验的总结果数为4×4＝16，A，B同时发生的结果数为4，
所以P（A∩B）0，A，B不互斥，B错误；
对于C，B发生的结果数为2×2+2×2＝8，P（B），
P（AB）＝P（A∪B）P（A）×P （B），所以事件A与事件B相互独立，C正确；
对于D，P（A∪B）＝P（A）+P（B）﹣P（A∩B），D正确．
故选：CD．
（多选）12．（5分）如图，在边长为4的正方形ABCD中，点E是AB的中点，点F是BC的中点，点P是AD上的动点，将△ADE，△CDF分别沿DE，DF折起，使A，C两点重合于点G，则下列结论正确的是（ ）
A．BG⊥EF
B．G到平面DEF的距离为
C．若BG∥面EFP，则二面角D﹣EF﹣P的余弦值为
D．四面体G﹣DEF外接球表面积为24π
【解答】解：由题意可得GE＝GF＝2，连接EF，BD，设EF∩BD＝H，
由正方形的对称性可得H为EF的中点，则EF⊥GH，EF⊥BD，
所以EF⊥平面BDG，即有EF⊥BG，故A正确；
由题意可得DG⊥GE，DG⊥GF，即有DG⊥平面GEF，
VD﹣GEF42×2．
设G到平面DEF的距离为d，由S△DEF26，
所以VD﹣GEF＝VG﹣DEFd×6，解得d，故B错误；
若BG∥面EFP，平面BGD∩平面EFP＝PH，可得BG∥PH，
由BG⊥EF，可得PH⊥EF，又EF⊥DH，则∠PHD为二面角D﹣EF﹣P的平面角．
由正方形ABCD可得BD＝4，即有BH，DH＝3，
而，DG＝4，可得DP＝3，
又PH，则cs∠DHP，故C正确；
由于GE＝FG＝2，EF＝2，可得GE⊥GF，又GE⊥GD，GF⊥GD，
可把三棱锥G﹣DEF补成以GE，GF，GD为棱的长方体，
可得四面体G﹣DEF外接球的半径R，
则四面体G﹣DEF外接球表面积为4πR2＝24π，故D正确．
故选：ACD．
三、填空题：本大题共4个小题，每小题5分，共20分．
13．（5分）已知，则sin2θ＝ ．
【解答】解：cs（θ），
可得（csθ﹣sinθ），
两边平方化简得：1﹣2csθsinθ，
∴sin2θ．
故答案为：．
14．（5分）以棱长为1的正方体各面的中心为顶点，构成一个正八面体，那么这个正八面体的表面积是 ．
【解答】解：根据题意，以棱长为1的正方体各面的中心为顶点，构成一个正八面体，设所得正八面体的棱长为a，
则这个正八面体的中截面（垂直平分相对顶点连线的界面）是正方形，
且正方形对角线长等于正方体的棱长1，则1，解可得a，
又由该正八面体的每个面都是等边三角形，
则其表面积S＝8×（）．
故答案为：．
15．（5分）一个袋子中有大小和质地相同的5个球，其中有3个红色球，2个白色球，从袋中不放回地依次随机摸出2个球，则第2次摸到红色球的概率为 ．
【解答】解：袋子中有相同的5个球，3个红球，2个白球，
不放回地依次随机摸出2个球，
∴第1次可能摸到1白色球或1红色球
∴第2次摸到红色球的概率为：，
故答案为：．
16．（5分）在△ABC中，（2m，m+5），（csα，sinα），（m∈R，α∈R），若对任意的实数t，恒成立，则BC边的最小值是 ．
【解答】解：根据题意，若对任意的实数t，恒成立，
即||恒成立，则必有BC⊥AC，
又（2m，m+5），（csα，sinα），
则||，||＝1，
则||

，
当m＝﹣1时，BC边的最小值为．
故答案为：．
三、解答题：本大题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤．
17．（10分）如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，侧面ADP是正三角形，侧面ADP⊥底面ABCD，M是DP的中点．
（1）求证：AM⊥平面CDP；
（2）求直线BP与底面ABCD所成角的正弦值．
【解答】（1）证明：因为侧面ADP是正三角形，且M是DP的中点，
所以AM⊥PD，
因为底面ABCD为正方形，所以AD⊥CD，
又侧面ADP⊥底面ABCD，侧面ADP∩底面ABCD＝AD，CD⊂底面ABCD，
所以CD⊥平面ADP，
因为AM⊂平面ADP，所以CD⊥AM，
又PD∩CD＝D，PD、CD⊂平面CDP，
所以AM⊥平面CDP．
（2）解：取AD的中点E，连接BE，PE，则PE⊥AD，
因为侧面ADP⊥底面ABCD，侧面ADP∩底面ABCD＝AD，PE⊂平面ADP，
所以PE⊥平面ABCD，
所以∠PBE即为直线BP与底面ABCD所成角，
设正方形ABCD的边长为2，则PE，BE，
所以PB2，
在Rt△PBE中，sin∠PBE，
故直线BP与底面ABCD所成角的正弦值为．
18．（12分）已知在△ABC中，A+B＝2C，2sin（A﹣C）＝sinB．
（1）求sinA；
（2）设，求△ABC的面积．
【解答】解：（1）因为A+B＝2C，而A+B+C＝π，可得C，
又因为2sin（A﹣C）＝sinB＝sin（π﹣A），
即sinAcsAcsAsinA，
可得sinA＝3csA，可得tanA＝3，
A∈（0，π），
可得sinA；
（2）由正弦定理可得，
所以a•sinA•6，csA，
sinB＝sin（π﹣A）csAsinA••，
所以S△ABCacsinB6×26．
19．（12分）已知向量，，记函数．
（1）求使函数f（x）≤0成立的x的取值集合；
（2）已知α，β均为锐角，，，求sin（2α﹣β）的值．
【解答】解：（1），，．
则f（x）2（1﹣csx）﹣1


，
∵f（x）≤0，
∴，即，k∈Z，解得，k∈Z，
故使函数f（x）≤0成立的x的取值集合为{x|，k∈Z}；
（2），
则，解得，
α为锐角，
则csα，
α，β均为锐角，
则α﹣β∈，
，
则，
故sin（2α﹣β）＝sin[（α﹣β）+α]＝sin（α﹣β）csα+cs（α﹣β）sinα．
20．（12分）某地区为了解市民的心理健康状况，随机抽取了n位市民进行心理健康问卷调查，将所得评分百分制按国家制定的心理测评评价标准整理，得到频率分布直方图．已知调查评分在[70，80）中的市民有200人．
心理测评评价标准
（1）求n的值及频率分布直方图中t的值；
（2）该地区主管部门设定预案：若市民心理健康指数的平均值不低于0.75，则只需发放心理指导资料，否则需要举办心理健康大讲堂．根据调查数据，判断该市是否需要举办心理健康大讲堂，并说明理由．（每组的每个数据用该组区间的中点值代替，心理健康指数＝调查评分÷100）
（3）在抽取的心理等级为D的市民中，按照调查评分的分组，分为2层，通过分层随机抽样抽取3人进行心理疏导．据以往数据统计，经心理疏导后，调查评分在[40，50）的市民的心理等级转为B的概率为，调查评分在[50，60）的市民的心理等级转为B的概率为，假设经心理疏导后的等级转化情况相互独立，求在抽取的3人中，经心理疏导后恰有一人的心理等级转为B的概率；
【解答】解：（1）易知调查评分在[70，80）中的市民有200人，
而评分在[70，80）中的频率为10×0.020＝0.2，
所以n1000，
而10（t+0.004+7t+0.020+0.035+0.025）＝1，
解得t＝0.002；
（2）市民心理健康调查评分的平均值10（45×0.002+55×0.004+65×0.014+75×0.020+85×0.035+95×0.025）＝80.7，
则市民心理健康指数平均值为0.807＞0.75，
所以只需发放心理指导资料，不需要举办心理健康大讲堂；
（3）因为评分在[40，50）中的人数是评分在[50，60）中人数的一半，
若通过分层随机抽样抽取3人进行心理疏导，
此时评分在[40，50）内的有1人，在[50，60）内的有2人，
记“在抽取的3人中，经心理疏导后恰有一人的心理等级转为B”为事件A，
因为经心理疏导后的等级转化情况相互独立，
所以P（A），
则在抽取的3人中，经心理疏导后恰有一人的心理等级转为B的概率为．
21．（12分）如图，在棱长为3的正方体ABCD﹣A'B'C'D'中，M为AD的中点．
（1）求证：DB'∥平面BMA'；
（2）在体对角线DB'上是否存在动点Q，使得AQ⊥平面BMA'？若存在，求出DQ的长；若不存在，请说明理由．
【解答】解：（1）证明：连接B'A，交A'B于点E，连接EM，
在正方体中，可得E为AB'的中点，而M是AD的中点，
在△DAB'中，ME∥DB'，
ME⊂平面BMA'，DB'⊄平面BMA'，
可证得DB'∥平面BMA'；
（2）对角线DB'上存在点Q，且DQ，使得AQ⊥平面BMA'，
证明如下：建立如图所示空间直角坐标系：
A（0，0，0），B（3，0，0），D（0，3，0），则M（0，，0），A'（0，0，3），B'（3，0，3），
则（﹣3，，0），（﹣3，0，3），（0，3，0），
设λλ（﹣3，3，﹣3）＝（﹣3λ，3λ，﹣3λ），（﹣3λ，3λ+3，﹣3λ），
因为AQ⊥平面BMA'，
所以，即，解得λ，
即Q（1，2，1），
所以DQDB'3
即在对角线DB'上存在点Q，且DQ，使得AQ⊥平面BMA'．
22．（12分）设函数f（x）的定义域为D，对于区间I＝[a，b]（a＜b，I⊆D），若满足以下两条性质之一，则称I为f（x）的一个“Ω区间”．
性质1：对任意x∈I，有f（x）∈I；
性质2：对任意x∈I，有f（x）∉I．
（1）分别判断区间[1，2]是否为下列两函数的“Ω区间”（直接写出结论）；
①y＝3﹣x；②；
（2）若[0，m]（m＞0）是函数f（x）＝﹣x2+2x的“Ω区间”，求m的取值范围；
（3）已知定义在R上，且图象连续不断的函数f（x）满足：对任意a，b∈R，且a＜b，有f（a）﹣f（b）＞b﹣a．求证：f（x）存在“Ω区间”，且存在x0∈R，使得x0不属于f（x）的任意一个“Ω区间”．
【解答】解（1）①中，函数y＝3﹣x，当x∈[1，2]时，可得y∈[1，2]，
所以区间[1，2]是函数y＝3﹣x的一个“Ω区间”；
②中，函数，当x∈[1，2]时，可得y∈[2，4]，此时不满足f（x）∉[1，2]，也不满足f（x）∈[1，2]，
所以区间[1，2]不是函数的一个“Ω区间”；
所以①是（满足性质1），②不是；
（2）记I＝[0，m]，S＝{f（x）|x∈I}，
可得f（0）＝0∈[0，m]，
故若I为f（x）的“Ω区间”，
则不满足性质②，必满足性质①，即S⊆I；
由f（x）＝﹣x2+2x＝﹣（x﹣1）2+1，
当0＜m＜1时，f（x）在[0，m]上单调递增，
且f（m）﹣m＝﹣m2+2m﹣m＝﹣m（m﹣1）＞0，
即f（m）＞m，所以S＝[0，f（m）]不包含于I＝[0，m]，不合题意；
当1≤m≤2时，S＝[f（0），f（1）]＝[0，1]⊆[0，m]＝I，符合题意；
当m＞2时，f（m）＜f（2）＝0，所以f（x）∉I，不合题意；
综上所述，1≤m≤2，
即实数m的取值范围是[1，2]；
（3）证明：对于任意区间I＝[a，b]（a＜b），记S＝{f（x）|x∈I}，
由已知得f（x）在I上单调递减，故S＝[f（b），f（a）]，
因为f（a）﹣f（b）＞b﹣a，
即S的长度大于I的长度，故不满足性质①，
所以若I为f（x）的“Ω区间”，必满足性质②，这只需S∩I＝∅，
即只需f（a）＜a或f（b）＞b，
由f（x）＝x显然不恒成立，所以存在常数c使得f（c）≠c，
如f（c）＜c，取a＝c，区间I＝[a，b]（a＜b）满足性质②；
如f（c）＞c，取b＝c，区间I＝[a，b]（a＜b）满足性质②；
综上，函数f（x）一定存在“Ω区间”；
记g（x）＝f（x）﹣x，则g（x）图象连续不断，下证明g（x）有零点：
因为f（x）在R上是减函数，所以g（x）在R上是减函数，记f（0）＝t；
若t＝0，则x0＝0是g（x）的零点，
若t＞0，则f（t）＜f（0）＝t，即g（0）＞0，g（t）＜0，
由零点存在性定理，可知存在x0∈（0，t），使得g（x0）＝0，
若t＜0，则f（t）＞f（0）＝t，即g（0）＜0，g（t）＞0，
由零点存在性定理，可知存在x0∈（t，0），使得g（x0）＝0，
综上，g（x）有零点x0，即f（x0）＝x0，
因为f（x）的所有“Ω区间”I都满足性质②，故x0∉I（否则f（x0）＝x0∈I，与性质②不符），
即x0不属于f（x）的任意一个“Ω区间”．调查评分
[0，40）
[40，50）
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
心理等级
E
D
B
B
A
调查评分
[0，40）
[40，50）
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
心理等级
E
D
B
B
A