清单03 整式的乘除与因式分解 全章复习 （3个考点梳理+13种题型解读）（原卷版+解析版）

这是一份清单03 整式的乘除与因式分解 全章复习 （3个考点梳理+13种题型解读）（原卷版+解析版），文件包含清单03整式的乘除与因式分解全章复习3个考点梳理+13种题型解读原卷版docx、清单03整式的乘除与因式分解全章复习3个考点梳理+13种题型解读解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

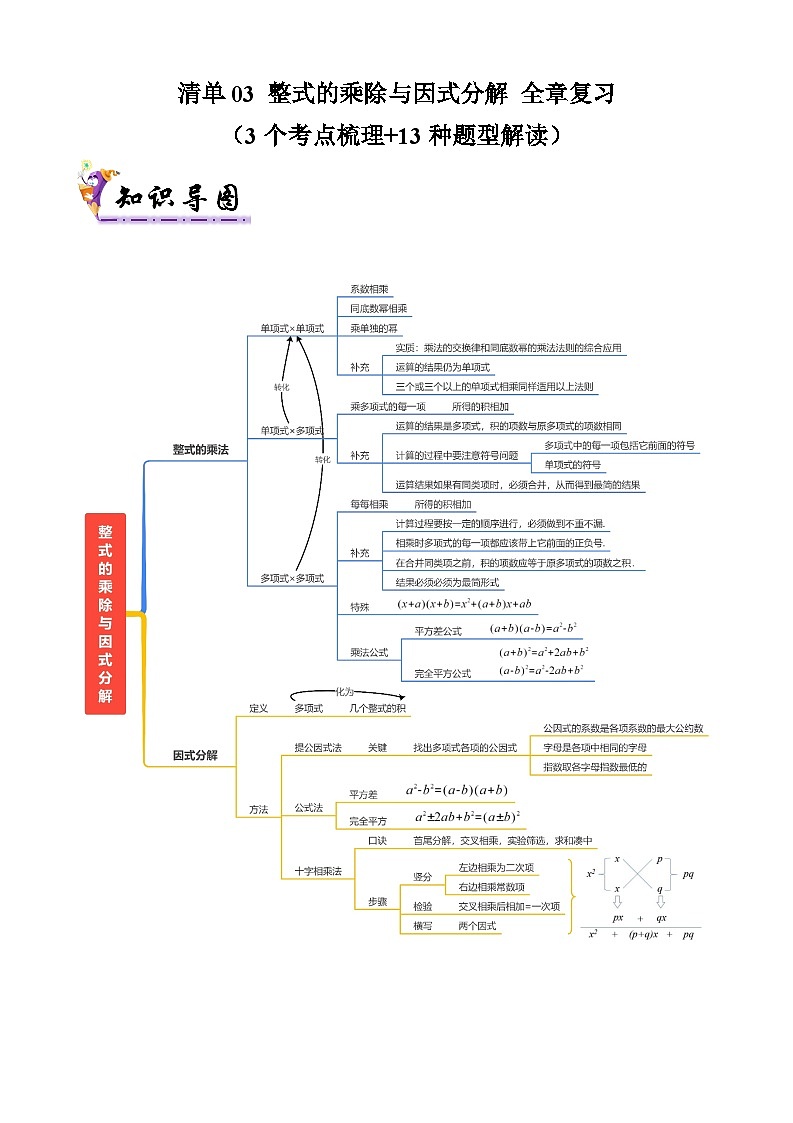
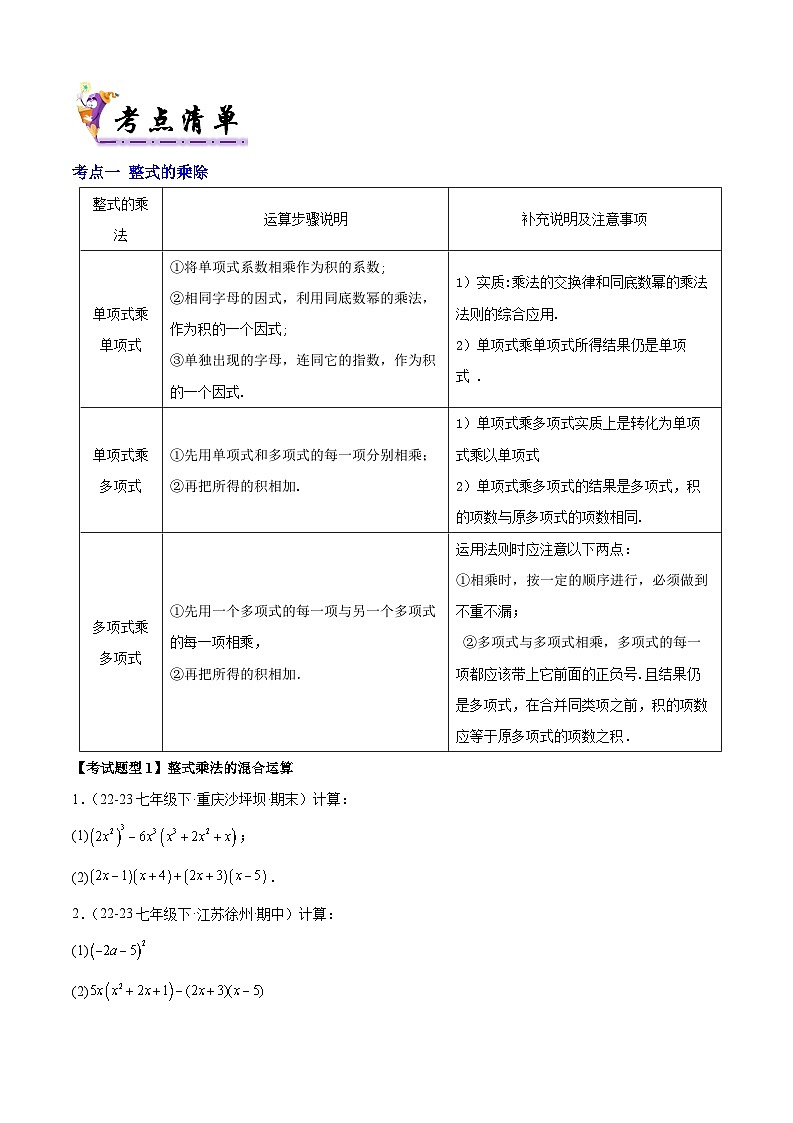
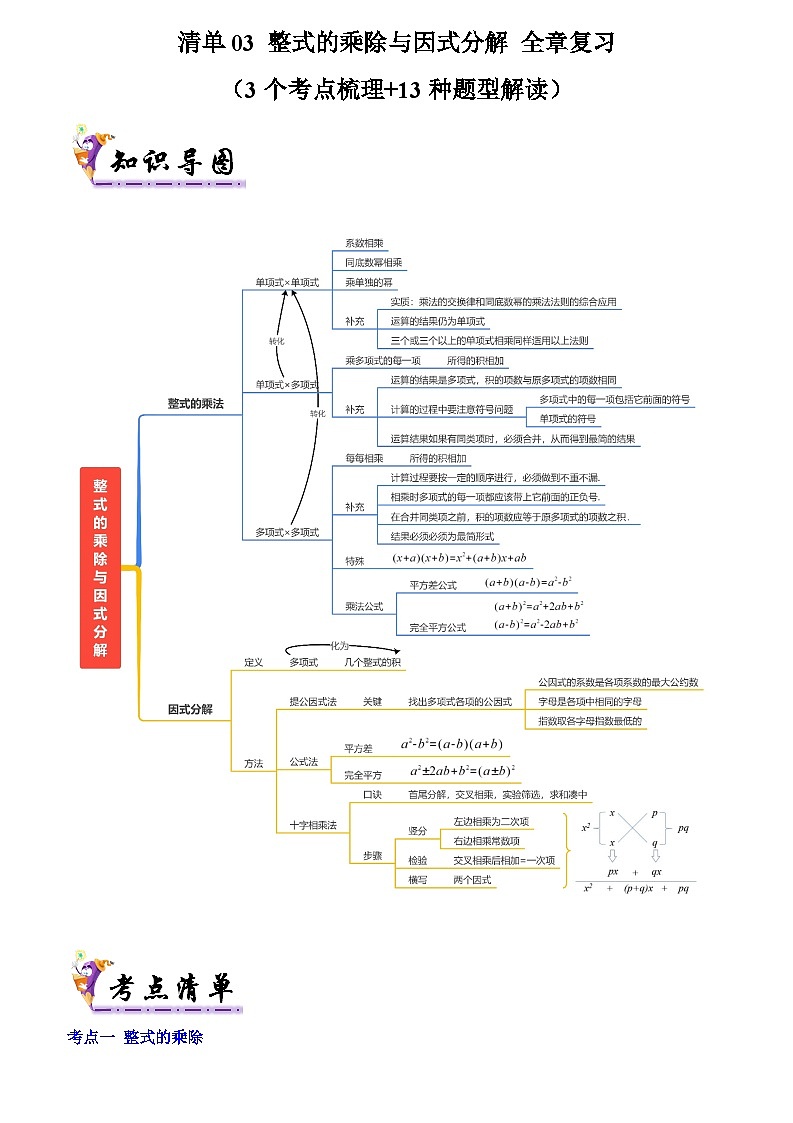
考点一 整式的乘除
【考试题型1】整式乘法的混合运算
1．（22-23七年级下·重庆沙坪坝·期末）计算：
(1)；
(2)．
【答案】(1)
(2)
【分析】（1）根据幂的运算性质和单项式乘以多项式展开化简即可；
（2）根据多项式乘以多项式化简即可；
【详解】（1）解：原式
（2）原式
【点睛】本题主要考查了整式的乘法运算，掌握相关法则和公式是解题的关键．
2．（22-23七年级下·江苏徐州·期中）计算：
(1)
(2)
【答案】(1)
(2)
【分析】（1）利用完全平方公式计算即可．
（2）利用整式的乘法法则计算即可．
【详解】（1）原式
；
（2）原式
【点睛】本题考查整式的乘法，和完全平方公式的计算，熟练地掌握整式乘法的运算法则是解题的关键．
3．（22-23七年级下·重庆沙坪坝·阶段练习）计算
(1)
(2)
(3)
(4)
【答案】(1)6
(2)
(3)
(4)
【分析】（1）先分别计算负整数次幂、乘方、零次幂，再进行加减运算；
（2）利用平方差公式计算；
（3）先计算多项式的乘法，再合并同类项；
（4）按照多项式乘多项式法则计算．
【详解】（1）解：
（2）解：
（3）解：
（4）解：
【点睛】本题考查多项式乘多项式、平方差公式、完全平方公式、有理数的乘方运算、零次幂等，解题的关键是掌握各项运算法则并正确计算．
【考试题型2】利用整式乘法求字母或代数式的值
4．（22-23七年级·上海·假期作业）先化简，再求值：，其中．
【答案】， 1
【分析】先计算积的乘方，再根据单项式乘以单项式的计算法则求解即可．
【详解】解：
，
当时，原式．
【点睛】本题主要考查了单项式乘以单项式，积的乘方和代数式求值，正确计算是解题的关键．
5．（20-21八年级上·全国·课后作业）有理数x，y满足条件，求代数式的值．
【答案】192
【分析】由非负数的性质，得到方程组，然后求出x、y的值，即可求出代数式的值．
【详解】解：∵，
∴，
解得：．
．
当，时，
原式．
【点睛】本题考查了解二元一次方程组，求代数式的值，绝对值的非负性，解题的关键是由非负性求出x、y的值，从而进行解题．
6．（22-23七年级下·四川成都·期中）先化简，再求值：，其中，．
【答案】，
【分析】本题考查了乘法公式，单项式乘多形式，熟练掌握公式和运算法则是解答本题的关键．先根据乘法公式，单项式乘多形式的运算法则计算，再合并同类项，然后把，代入计算即可．
【详解】解：
，
将，代入，
原式．
【考试题型3】已知多项式乘积不含某项求字母的值
7．（23-24八年级上·河南新乡·阶段练习） 已知关于x的多项式与的乘积的展开式中不含项，且的系数为2，求的值．
【答案】
【分析】本题考查多项式乘以多项式，解题的关键是明确不含x的二次项，则二次项的系数为0．
根据多项式乘以多项式法则进行运算，再利用关于x的多项式与的乘积的展开式中不含项，且的系数为2建立方程，即可求解．
【详解】解：
∵展开式中不含项，且的系数为2
∴，，解得，
∴．
8．（23-24八年级上·四川眉山·期中）若的积中不含项与项，
(1)求、的值；
(2)求代数式的值．
【答案】(1)，
(2)33
【分析】本题考查了多项式乘多项式，代数式求值，熟练掌握多项式乘多项式运算法则是解题的关键．
（1）利用条件中积不含项与项，将积算出来后，令相应的项系数为0即可求解；
（2）利用第（1）问中的结果，代入求值．
【详解】（1）解：
，
积中不含项与项，
，
．
（2）解：由（1）知：，，
∴原式．
【考试题型4】整式乘法的错看/错解问题
9．（23-24八年级上·河南南阳·阶段练习）甲、乙二人共同计算一道整式乘法：，由于甲抄错为，得到的结果为；而乙抄错为，得到的结果为．
(1)你能否知道式子中的a，b的值各是多少？
(2)请你计算出这道整式乘法的正确答案．
【答案】(1)，
(2)
【分析】（1）按照甲、乙两人抄的错误的式子进行计算，得到，，解关于的方程组即可求出a、b的值；
（2）把a、b的值代入原式求出整式乘法的正确结果．
【详解】（1）根据题意可知，甲抄错为，得到的结果为，
那么，
可得
乙抄错为，得到的结果为，
可知
可得，
解关于的方程组，可得，；
（2）正确的式子：
【点睛】本题主要是考查多项式的乘法以及二元一次方程组，掌握多项式乘多项式运算法则是正确解决问题的关键．
10．（22-23七年级下·全国·假期作业）小红准备完成题目：计算，她发现第一个因式的一次项系数被墨水遮挡住了．
(1)她把被遮住的一次项系数猜成3，请你完成计算：；
(2)老师说：“你猜错了，这个题目的正确答案是不含一次项的，”请通过计算说明原题中被遮住的一次项系数是多少？
【答案】(1)
(2)2
【分析】（1）根据多项式乘以多项式的计算法则求解即可；
（2）设第一次因式的一次项系数为a，则原题目变为，根据多项式乘以多项式的计算法则计算出结果，再根据结果不含一次项即一次项系数为0进行求解即可．
【详解】（1）解：
；
（2）解：设第一次因式的一次项系数为a，则原题目变为，
，
∵的计算结果不含一次项，
∴，
∴，
∴被遮住的一次项系数是2．
【点睛】本题主要考查了多项式乘以多项式，熟知相关计算法则是解题的关键．
11．（23-24八年级上·湖南长沙·期中）小雅同学计算一道整式除法：，由于她把除号错写成了乘号，得到的结果为
(1)直接写出a、b的值： ， ．
(2)这道除法计算的正确结果是 ；
(3)若，，计算（2）中代数式的值．
【答案】(1)，
(2)
(3)
【分析】本题考查了整式的乘法和除法以、因式分级以及代数式求值，熟练掌握相关运算法则是关键．
（1）按题意将除法运算改成乘法，计算，将乘积与对应系数相等，即可求出答案；
（2）根据多项式除以单项式法则计算即可；
（3）先将提公因式，再将，代入即可．
【详解】（1）解：由题意，，
∴，
解得，，
故答案为：；
（2）由题意，得
，
故答案为：；
（3）
∴原式．
12．（23-24八年级上·江西赣州·阶段练习）某同学在计算一个多项式A乘时，因抄错运算符号，算成了加上，得到的结果是，请求出正确的运算结果．
【答案】
【分析】本题考查了整式的加减，多项式乘单项式；
首先根据题意求出原多项式，再根据多项式乘单项式的运算法则进行计算．
【详解】解：∵算成了加上，得到的结果是，
∴原多项式为，
∴．
【考试题型5】多项式乘多项式与图形面积
13．（22-23七年级下·河南郑州·阶段练习）如图，某校有一块长为米，宽为米，中间是边长为米的正方形草坪，学校计划将活动场地（阴影部分）进行硬化．
(1)用含a，b的代数式表示需要硬化的面积并化简；
(2)若，，硬化成本为每平方米50元，则完成硬化共需多少钱
【答案】(1)
(2)7000元
【分析】本题主要考查了整式四则混合运算的应用，解题的关键是根据题意列出算式，准确计算．
（1）用长方形的面积减去中间正方形的面积，得出结果即可；
（2）根据，，求出活动场地的面积，然后再求出硬化需要的费用即可．
【详解】（1）解：由图得，阴影面积为：
；
（2）解：把，代入得：（平方米），
即阴影部分的面积为平方米，
完成硬化共需要的费用为：
（元），
答：完成硬化共需元钱．
14．（22-23八年级上·北京朝阳·期末）在“整式乘法与因式分解”这一章的学习过程中，我们常采用构造几何图形的方法对代数式的变形加以说明．例如，利用图1中边长分别为，的正方形，以及长为，宽为的长方形卡片若干张拼成图2（卡片间不重叠、无缝隙），可以用来解释完全平方公式：
请你解答下面的问题：
(1)利用图1中的三种卡片若干张拼成图3，可以解释等式： ；
(2)利用图1中三种卡片若干张拼出一个面积为的长方形，请你分析这个长方形的长和宽．
【答案】(1)；
(2)图形见解析，长方形的长为，宽为．
【分析】（1）本题考查多项式乘法的几何形式，根据图形，利用直接求和间接求两种方法，列出等式即可；
（2）本题考查考查了因式分解的应用，根据已知等式画出相应的图形，然后根据图形写出长方形的长和宽即可．
【详解】（1）解：由图知，；
故答案为：．
（2）解：，
由图知，长方形的长为，宽为．
15．（23-24八年级上·四川内江·阶段练习）数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释．如图1，有足够多的三种纸片：边长为a的小正方形（A类），长为、宽为a的长方形（B类）以及边长为b的正方形（C类）．
用图1中的A类纸片2张，B类纸片3张、C类纸片1张可以拼出图2所示的长方形．根据长方形的面积，可以用来解释整式乘法：，也可以解释因式分解：

(1)如果要拼成一个长为（），宽为的大长方形，则需要B类纸片 张，C类纸片 张；
(2)若用4张B类纸片围成图3所示的图形，设外围大正方形的边长为x，内部小正方形的边长为y，则下列等式中：①；②；③；④；⑤，正确的有 ；（写出所有正确结论的序号）
(3)如果取若干张纸片（三种都要取）拼成一个长方形，使其面积为，请在虚框中画出图形，并根据所画图形将多项式分解因式；
(4)如果取若干张纸片（三张都要取）刚好拼成一个长方形，其面积为，求m的值．
【答案】(1)4，3；
(2)①③④⑤；
(3)图见详解，；
(4)或或．
【分析】本题考查整式乘法与图形面积的关系：
（1）根据长方形的长和宽求出面积即可得到答案；
（2）根据图形表示出两个正方形边长与，的关系，，结合面积加减计算即可得到答案；
（3）根据整式得到两个大正方形，两个小正方形，五个长方形组合即可得到答案；
（4）根据因式分解平方项凑长宽展开求解即可得到答案；
【详解】（1）解：由题意可得，
，
∴需要，一个A类图形，4个B类图形，3个C类图形，
故答案为：4，3；
（2）解：由图形可得，
，，故①正确，
∴，，
，故②错误，④⑤正确，
由图形可得，，
∴，故③正确，
故答案为：①③④⑤；
（3）解：由题意可得，图形如图所示，

∴；
（4）解：由题意可得，
①当，，
②当，，
③当，，
故答案为：或或．
考点二 乘法公式
平方差公式的几何背景
1）意义：运用几何图形直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．
2）通过面积法推导完全平方公式：
如图1所示，左侧涂色部分的面积为，右侧涂色部分的面积为，所以可以得到.
3）常见验证平方差公式的几何图形
完全平方公式的几何背景
1）意义：运用几何图形直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．
2）通过面积法推导完全平方公式：
①如图甲所示是一个边长为a+b的正方形，面积为，它的面积还可以看成是由两个小正方形与两个长方形的和，即，所以可以得到；
②如图乙所示，边长为a-b的小正方形的面积是，它的面积还可以看成是由大的正方形面积减去两个小的长方形面积，即，所以可以得到.
【考试题型6】利用乘法公式化简求值
16．（20-21九年级下·湖南长沙·开学考试）先化简，再求值:，其中．
【答案】，8．
【分析】本题考查了整式的化简求值，熟练掌握平方差公式、完全平方公式以及单项式乘以多项式的法则是解题的关键．
先利用平方差公式、完全平方公式以及单项式乘以多项式的法则进行化简，再代入求值．
【详解】解：
=
=，
当时，原式=．
17．（23-24八年级上·河南漯河·阶段练习）先化简，再求值：其中．．
【答案】，
【分析】题目主要考查整式的乘法运算及化简求值，利用平方差公式及整式的乘法先化简，然后代入求解即可，熟练掌握运算法则是解题关键．
【详解】解：
，
当时，
原式
．
18．（22-23七年级下·江苏盐城·期中）化简求值：，其中．
【答案】，
【分析】本题考查了整式的混合运算-化简求值．先利用完全平方公式、平方差公式、多项式乘以多项式，然后再合并同类项，代入数值即可．
【详解】解：
，
当时，原式．
【考试题型7】乘法公式与几何图形
19．（23-24八年级上·安徽阜阳·阶段练习）如图，图1为边长为a的大正方形中有一个边长为b的小正方形，图2是由图1中的阴影部分拼成的一个长方形．
(1)设图1中阴影部分的面积为，图2中阴影部分的面积为，则______，______（请用含a，b的代数式表示，只需表示，不必化简）．
(2)以上结果可以验证哪个乘法公式？这个乘法公式是______
(3)运用（2）中得到的公式，计算：．
【答案】(1)，
(2)
(3)
【分析】本题主要考查了平方差公式的几何背景，利用面积公式表示出图形阴影部分面积是解题的关键．
（1）图1中阴影部分面积用大正方形面积减去小正方形面积表示即可，图2中阴影部分面积用长方形面积公式表示即可；
（2）根据（1）的结果，即可得到答案；
（3）在原式前面乘以，运用（2）中得到的公式计算，即可得到答案．
【详解】（1）解：由图形可知，图1中阴影部分面积，图2中阴影部分面积，
故答案为：，；
（2）解：∵图1和图2中的阴影部分面积相等，
∴以上结果可以验证乘法公式为：，
故答案为：；
（3）解：
．
20．（22-23七年级下·广东茂名·期末）如图1所示，边长为a的大正方形中有一个边长为b的小正方形，如图2是由图1中阴影部分拼成的一个长方形．

(1)请你分别表示出这两个图形中阴影部分的面积：___________，___________；（只需表示，不必化简）；
(2)请问以上结果可以验证哪个乘法公式？___________；
(3)试利用这个公式计算：
①；
②；
③．
【答案】(1)，
(2)
(3)①；②；③1
【分析】（1）图①中阴影部分面积等于大正方形面积减去小正方形面积；图②中阴影部分面积等于长为，宽为的长方形面积，据此求解即可；
（2）根据图①和图②中阴影部分面积相等即可得到答案；
（3）①等式前面乘以，利用平方差公式求解即可；
②等式前面乘以，利用平方差公式求解即可；
③把原式变形为利用平方差公式求解即可．
【详解】（1）解：由题意得，，
故答案为：，；
（2）解：∵图①和图②中阴影部分面积相等，
∴，
故答案为：；
（3）解：①原式，
，
，
②原式
．
③原式
．
【点睛】本题主要考查了平方差公式在几何图形中的应用，熟知平方差公式是解题的关键．
21．（22-23七年级下·浙江金华·期中）已知图甲是一个长为，宽为的长方形，沿图甲中虚线用剪刀均匀分成四个小长方形
(1)请用两种不同的方法，求图乙中阴影部分的面积（用含a、b的代数式表示，不用化简） 、 ；
(2)观察图乙，并结合（1）中的结论，，之间的相等关系式是 ；
(3)根据（2）中的等量关系解决如下问题：当，时，求的值．
【答案】(1)，
(2)
(3)16
【分析】本题考查列代数式，完全平方公式的应用．利用数形结合的思想是解题关键．
（1）由正方形面积公式直接求出阴影部分面积：；利用大正方形面积减去四个长方形面积：；
（2）根据图中阴影部分的面积不变列等式即可；
（3）根据（2）所求式子求解即可．
【详解】（1）解：方法①：直接利用正方形面积公式求阴影部分面积：，
方法②：利用大正方形面积减去四个长方形面积：．
故答案为：，；
（2）解：因为图中阴影部分的面积不变，所以，
故答案为：；
（3）解：由（2）得：，
∵，，
∴．
22．（22-23七年级下·江苏宿迁·期中）在学习《整式乘法与因式分解》一章时，我们从计算图形面积入手，利用两种不同的方法计算同一个图形的面积，这样就可以得到一个等式．从而进一步得到一些整式乘法法则、乘法公式，解决一些问题．这种解决问题的方法称之为面积法．
(1)如图1，边长为a的正方形纸片，在其右边和下边同时剪去宽为b的长方形，计算剩余纸片（图中阴影部分）的面积，可得等式：________；
(2)两个边长分别为a、b、c的直角三角形和一个两直角边都是c的直角三角形拼成图2，试用不同的方法计算这个图形的面积，并对所得到的等式进行化简；
(3)利用（2）中的结论计算：在直角三角形中，一条直角边的长为6，斜边的长为10，求另一直角边b的长度；
(4)如图3，在直角三角形中，，，垂足为D．且，．求的长．
【答案】(1)
(2)这个图形的面积是；化简为
(3)
(4)
【分析】（1）用两种不同方式计算阴影部分面积即可求解；
（2）用三个直角三角形可得面积，直接利用梯形可得面积，由此可得等式，化简即可；
（3）直接利用（2）中等式，代入求解即可；
（4）利用（2）中等式，再结合等面积法求解即可．
【详解】（1）解：由题意可得阴影部分面积为：，
阴影部分面积为：，
∴，
故答案为：；
（2）由题意得：，
，
，
∴；
（3）由（2）得，得：，
即：，
解得：；
（4）由（2）得，
∴
∴
∵：
∴
∴．
【点睛】本题主要考查了完全平方公式，结合图形得出关系式是解题的关键．
【考试题型8】通过对乘法公式变形求值
23．（23-24八年级上·四川眉山·期中）已知，求下列各式的值：
(1)；
(2)；
(3)．
【答案】(1)；
(2)；
(3)．
【分析】本题考查了完全平方公式的应用，解题的关键是熟知完全平方公式的变形．
（1）利用完全平方公式得到，进一步计算即可求解；
（2）利用完全平方公式求得，进一步计算即可求解；
（3）解方程组或，求得的值，代入计算即可求解．
【详解】（1）解：∵，
即，
∴；
（2）解：∵，
∴；
（3）解：∵，又，
∴或，
解得或，
∴当时，；
当时，；
∴．
24．（23-24八年级上·四川巴中·期末）已知：，，求下列代数式的值：
(1)；
(2)．
【答案】(1)
(2)
【分析】本题考查了完全平方公式及其变形公式的运用，掌握公式形式是解题关键．
（1）根据，整体代入，即可求解；
（2）根据即可求解．
【详解】（1）∵，，
∴；
（2）∵，，
∴，
∴
25．（23-24八年级上·辽宁抚顺·期末）【发现问题】
小亮同学把图①长为、宽为的长方形，沿图中虚线用剪刀将其平均分为四个小长方形，然后拼成了如图②所示的正方形．
小亮进一步发现图②里面的小正方形的面积可以用两种方法去求，请写出小亮的两种方法所得的结果（结果用含m，n的代数式表示）
方法一： ；方法二： ；
【提出问题】
、之间有怎样的数量关系？
【分析问题】（完成下列填空）
分析一：因为上述两种方法都是求同一个正方形的面积，所以这两个面积的结果一定相等．
分析二：因为是两个数m与n和的完全平方，所①，
因为是两个数m与n差的完全平方，所以②，
由得 ；
类似的，由可得 ．
【解决问题】
（1）若，则 ；（直接写出结果）
（2）已知，求与的值．
【答案】发现问题：，；
提出问题：；
分析问题：； ；
解决问题：（1）；（2）4，
【分析】本题考查了完全平方公式的几何背景：利用几何图形之间的面积关系得到完全平方公式，解决问题的关键是利用整体代入的方法求代数式的值．
发现问题：观察得到长为m，宽为n的长方形的长宽之差即为阴影部分的正方形的边长，可以直接利用正方形的面积公式得到阴影部分面积；也可以用大正方形的面积减去4个长方形的面积得到图2中的阴影部分的正方形面积；
提出问题：利用“发现问题”中的结论进行计算可得；
分析问题：利用前面的结论计算可得；
解决问题：根据前面的结论代入计算即可．
【详解】发现问题：
方法一：图2中的阴影部分的正方形面积等于大正方形的面积减去4个长方形的面积，
故答案为： ；
方法二：图2中的阴影部分的正方形的边长等于，故阴影部分面积为；
故答案为：
（方法一和方法二可以调换）
提出问题：
；
故答案为：；
分析问题：
得．
可得．
故答案为：，；
解决问题：
（1）由可得，
，
，
，
则，
故答案为：；
（2）解：把，两个等式左右两边相减得∶
；
∵变形得整式的乘法
运算步骤说明
补充说明及注意事项
单项式乘单项式
①将单项式系数相乘作为积的系数;
②相同字母的因式，利用同底数幂的乘法，作为积的一个因式;
③单独出现的字母，连同它的指数，作为积的一个因式.
1）实质:乘法的交换律和同底数幂的乘法法则的综合应用.
2）单项式乘单项式所得结果仍是单项式 .
单项式乘多项式
①先用单项式和多项式的每一项分别相乘；
②再把所得的积相加.
1）单项式乘多项式实质上是转化为单项式乘以单项式
2）单项式乘多项式的结果是多项式，积的项数与原多项式的项数相同.
多项式乘多项式
①先用一个多项式的每一项与另一个多项式的每一项相乘，
②再把所得的积相加．
运用法则时应注意以下两点：
①相乘时，按一定的顺序进行，必须做到不重不漏；
②多项式与多项式相乘，多项式的每一项都应该带上它前面的正负号.且结果仍是多项式，在合并同类项之前，积的项数应等于原多项式的项数之积．