数学七年级下册6.3 实数背景图ppt课件

这是一份数学七年级下册6.3 实数背景图ppt课件，共20页。PPT课件主要包含了教学目标，新课导入，直径为1的圆，知识归纳，相反数，绝对值，aa0，新知探究，实数的运算顺序，实数的运算等内容，欢迎下载使用。

1.理解在实数范围内的相反数、倒数、绝对值的意义;（重点）2.掌握实数的运算法则, 解决有关实数的运算问题.（难点）

有理数中的几个重要概念:
思考: 无理数也有相反数吗？怎么表示？有绝对值吗？怎么表示？ 有倒数吗？怎么表示？
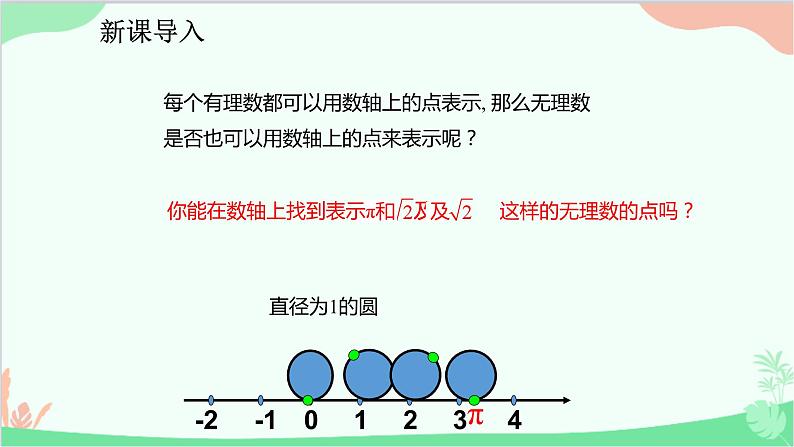
每个有理数都可以用数轴上的点表示, 那么无理数是否也可以用数轴上的点来表示呢？
你能在数轴上找到表示π和 及 这样的无理数的点吗？
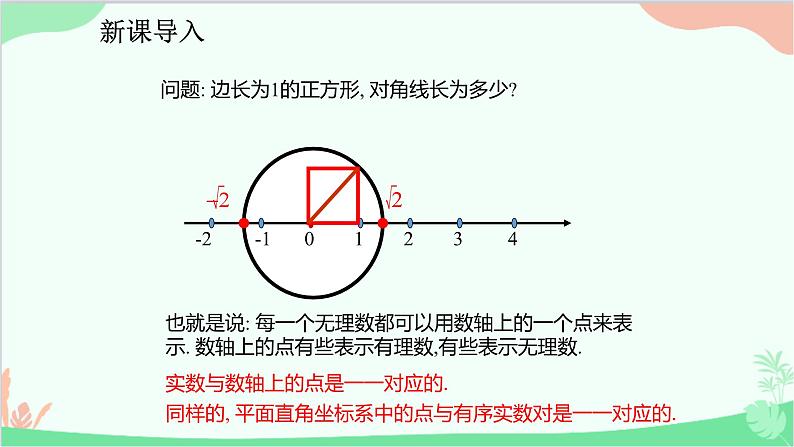
问题: 边长为1的正方形, 对角线长为多少?
也就是说: 每一个无理数都可以用数轴上的一个点来表示. 数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点是一一对应的.
同样的, 平面直角坐标系中的点与有序实数对是一一对应的.
实数 a 的相反数是 -a. 若a与b互为相反数, 则a＋b=0．
实数a的绝对值, 记为|a|, 它是一个非负实数．
-a（ a<0 ）
几何意义: |a|表示点 x 到原点0的距离． 而| a-b |表示点 a 与点 b 的距离．
（1）求 的相反数;
当数从有理数扩充到实数以后, 实数之间不仅可以进行加、减、乘、除、乘方运算, 又增加了非负数的开平方运算, 任意实数可以进行开立方运算. 进行实数运算时, 有理数的运算法则及性质等同样适用.
(1)先算乘方和开方;(2)再算乘除, 最后算加;(3)如果遇到括号, 则先进行括号里的运算.
例3: 计算下列各式的值.
小数部分：
整数部分与小数部分的差为
实数的性质及运算
实数 a 的相反数是- a, 若 a 与 b 互为相反数, 则a＋b=0．
实数 a 的绝对值, 记为|a|, 它是一个非负实数．
两种分类: ①根据实数的定义; ②根据实数的正负性.
实数与数轴上的点成一一对应关系.
(1) -2是负数.(2) π是正数.(3) 1-π是正数.
2.计算 +(- )的结果是 ( ) A.4 B.0 C.8 D.12
3. 的值是 ( ) A.5 B.-1 C. D.
4.如果05. 3的相反数是 .
7.点 A 在数轴上和原点相距3个单位, 点 B 在数轴上和原点相距
个单位, 则 A, B 两点之间的距离是 .
9.阅读下列材料: 如果一个数的 n ( n 是大于1的整数)次方等于a, 这个数就叫做 a 的 n 次方根, 即xn=a, 则x叫做a的n次方根. 如： 24=16, (-2)4=16, 则2, -2是16的4次方根, 或者说16的4次方根是 2和-2; 再如(-2)5=-32, 则-2叫做-32的5次方根, 或者说-32的5次 方根是-2. 回答问题： (1)64的6次方根是________, -243的5次方根是_______, 0的10次方根是_____; (2)归纳一个数的 n 次方根的情况.
答: 当 n 为偶数时, 一个正数的 n 次方根有两个,它们互为相反数; 当 n 为奇数时, 一个数的 n 次方根只有一个. 负数没有偶次方根. 0的 n 次方根是0.