初中数学人教版七年级下册7.2.2用坐标表示平移授课ppt课件

这是一份初中数学人教版七年级下册7.2.2用坐标表示平移授课ppt课件，共22页。PPT课件主要包含了教学目标，新课导入，新知探究，你发现了什么，知识归纳，移动的方向怎样，向右平移5个单位，课堂小结，用坐标表示平移，课堂小测等内容，欢迎下载使用。

1.掌握坐标变化与图形平移的关系;（重点）2.平面直角坐标系中, 点的平移与图形的平移的关系.（难点）
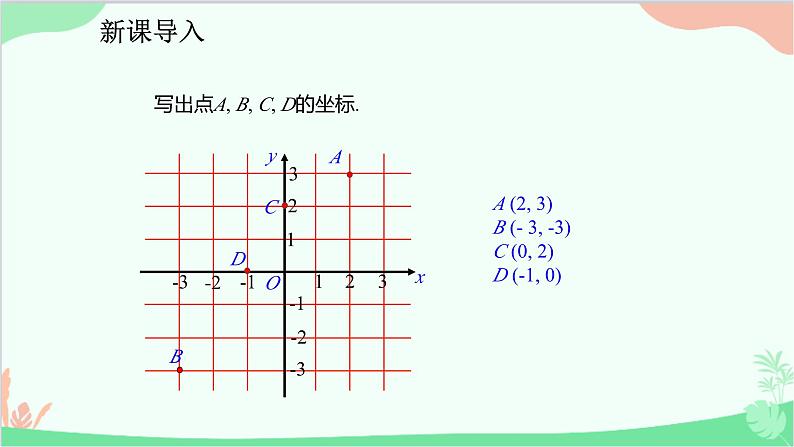
写出点A, B, C, D的坐标.
A (2, 3) 　 B (- 3, -3)　 C (0, 2)D (-1, 0)
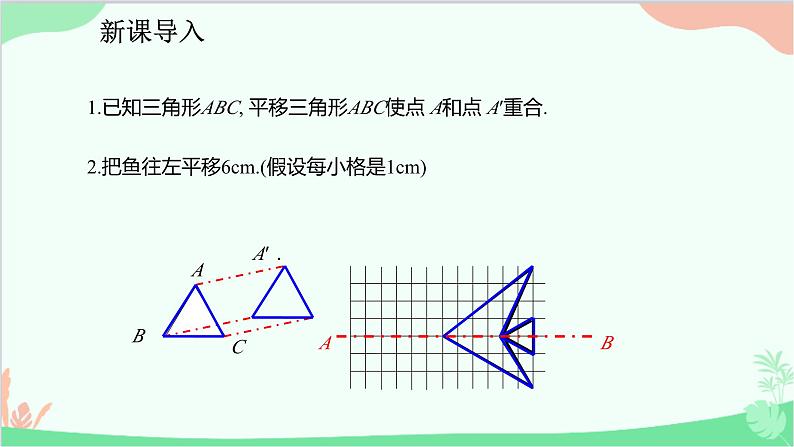
1.已知三角形ABC, 平移三角形ABC使点 A和点 A′重合.2.把鱼往左平移6cm.(假设每小格是1cm)
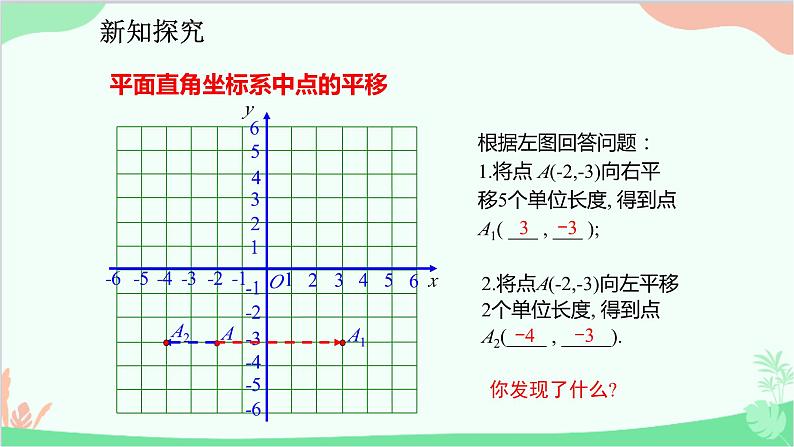
根据左图回答问题：1.将点 A(-2,-3)向右平移5个单位长度, 得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移2个单位长度, 得到点A2(____ , _____).
平面直角坐标系中点的平移
左、右平移横坐标变, 纵坐标不变, 变化规律是左减右加;数学表示: 将点(x, y)向右(向左)平移 a 个单位长度,可得到对应点(x+a, y)(或(x-a, y)).
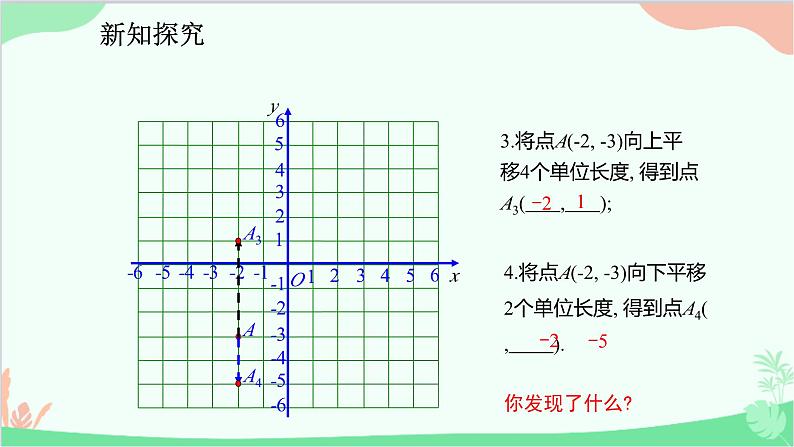
3.将点A(-2, -3)向上平移4个单位长度, 得到点A3( , );
4.将点A(-2, -3)向下平移2个单位长度, 得到点A4( , ).
上、下平移横坐标不变, 纵坐标变, 变化规律是上加下减.数学表示: 将点(x, y)向上(向下)平移 a 个单位长度,可得到对应点(x, y+a)(或(x, y-a)).
例1: 平面直角坐标系中, 将点 A(－3, -5)向上平移4个单位, 再向左平移3个单位到点B, 则点B的坐标为(　　) A.(1, -8) B.(1, -2) C.(-6, -1) D.(0, -1)
解析: 点A的坐标为(-3, -5), 将点 A向上平移4个单位, 再向左平移 3个单位到点B, 点B的横坐标是 -3 -3＝-6, 纵坐标为－5＋4 ＝-1, 即(-6, -1)．
平面直角坐标系中图形的平移
如图, △ ABC在坐标平面内平移后得到△A1B1C1.
2.写出△ ABC与△A1B1C1各点的坐标, 它们有怎样的变化？
A(-1, 3), B(-4, 2), C(-2, 1), A1(4, 3), B1(1, 2), C1(3, 1);平移后的对应点的横坐标增加了5, 纵坐标不变.
A2(4, -1), B2(1, -2), C2(3, -3);平移后的对应点的横坐标不变, 纵坐标减少了4.
3.如果△A1B1C1向下平移4个单位, 得到△A2B2C2, 写出各点的坐标, 它们有怎样的变化?
思考: △ABC 能否在坐标平面内直接平移后得到△A2B2C2 ？
一般地, 图形经过两次平移后得到的图形, 可以通过原来的图形作一次平移得到.
例2: 如图, 在平面直角坐标系中, P(a, b)是△ABC的边AC上一点, △ABC经平移后点P的对应点为P1(a＋6, b＋2).(1)请画出上述平移后的△A1B1C1, 并写出点A, C, A1, C1的坐标；
解：(1) △A1B1C1如图所示, 各点的坐标分别 为A(-3, 2), C(-2, 0), A1(3, 4), C1(4, 2).
(2)求出以 A, C, A1, C1为顶点的四边形的面积.
左、右平移横坐标变, 纵坐标不变, 变化规律是左减右加.
上、下平移横坐标不变, 纵坐标变, 变化规律是上加下减.
1.在平面直角坐标系中, 将点P(-2, 3)沿x轴方向向右平移3个单位得到 点Q, 则点Q的坐标是________, 该点在第______象限.
2.已知点A(-4, -6), 将点A先向右平移4个单位长度, 再向上平移6个单位长 度, 得到 A′, 则A′ 的坐标为________．
3.将点A(4, 3)向______平移_____个单位长度后, 其坐标为(4, -1)．
4.已知点A(-2, -3).（1）将点A向右平移5个单位长度得到点A₁, 则 点A₁点的坐标 是 ;（2）将点A向右平移6个单位长度得到点A₂, 则 点A₂点的坐标是 ;（3）将点A向右平移a(a>)个单位长度得到点Aₙ, 则 点Aₙ点的坐标是 ;（4）将点A向左平移a(a>)个单位长度得到点Aₙ′, 则 点Aₙ′点的坐标是 .
（-2-a , -3）
（-2+a , -3）
5.将三角形ABC向右平移2个单位 长度, 再向下平移3个单位长度, 得对应的三角形A1B1C1, 画出图 形并写出点A1, B1, C1的坐标.
答: 如图所示, 三角形A1B1C1就是所要画的三角形.
A1( 0, 2 ), B1(-3, -5), C1(5, 0 ).
6.如图, △ABC上任意一点 P(x0, y0) 经平移 后得到的对应点为P1(x0+2, y0+4), 将 △ABC作同样的 平移得到△A1B1C1. 求A1, B1, C1的坐标.
P1(x0+2, y0+4)
解: A(-3, 2)经平移后得到(-3+2, 2+4), 即A1(-1, 6); B(-2,-1)经平移后得到(-2+2, -1+4), 即B1(0, 3); C(3, 0)经平移后得到(3+2, 0+4), 即C1(5, 4).
7.如图, 在平面网格中每个小正方形边长为1． （1）线段CD是线段AB经过怎样的平移后得到的; （2）线段AC是线段BD经过怎样的平移后得到的.
解:（1）先将线段AB向右平移3个小格（或向下平移4个小格）, 再向下平移4个小格（或向右平移3个小格）, 得线段CD． （2）先将线段BD向右平移3个小格（或向下平移1个小格）, 再向下平移1个小格（或向左平移3个小格）, 得到线段AC．
8.如图, 在直角坐标系中, A(-3, 4), B(-1, -2), O为坐标原点, 把△AOB向右平 移3个单位, 得到△DEF．（1）求D, E, F 三点的坐标;（2）求△DEF 的面积.