












中考数学(云南卷)-2024年中考数学第三次模考试
展开2、二模考试大致在五月份,难度相对较大。这次考试主要检测学校以及学生在第一轮复习的成果,让老师和孩子找到问题的关键,是否存在基础不扎实,计算能力是否需要加强等等。然后找到解决方法,做到复习方法的改进,以及重难点的分布,复习的目标。
3、三模考试大概在中考前两周左右,三模是中考前的最后一次考前检验。三模学校会有意降低难度,目的是增强考生信心,难度只能是中上水平,主要也是对初中三年的知识做一个系统的检测,让学生知道中考的一个大致体系和结构。
2024年中考第三次模拟考试(云南卷)
数 学
(考试时间:120分钟 试卷满分:100分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
选择题(本大题共15个小题,每小题2分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.春节期间冰雪旅游大热,杭州的小明同学准备去旅游,考虑温差准备着装时,他查询气温,结果如图所示,杭州的气温是19℃,哈尔滨的气温是−14℃,则此刻两地的温差是( )
A. 33℃B. 19℃C. 14℃D. 5℃
2.中国向大海要水喝已成为现实.到目前为止我国已建成海水淡化工程123个,海水淡化能力每天超过1600000吨.数据1600000用科学记数法表示为( )
A. 16×105B. 160×105C. 1.6×105D. 1.6×106
3.如图,把一块含有45°的直角三角尺的两个锐角顶点放在直尺的对边上,若∠1=20°,则∠2的大小为( )
A. 20°B.25°C. 15°D. 30°
4.八年级物理教科书对压强做了如下定义,下面有关压强计算公式P=FS的结论:
①压力F不变时,压强P与受力面积S是反比例函数关系;
②受力面积S不变时,压强P与压力F是反比例函数关系;
③压强P不变时,压力F与受力面积S是反比例函数关系;
④受力面积S不变时,压强P与压力F是正比例函数关系,且图象经过第一、三象限.
其中正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
5.下列运算正确的是( )
A. 1x+1y=1x+yB. (−p2q)3=−p5q3
C. a⋅ b= abD. (a+b)2=a2+b2
6.如图,在△ABC中,DE//BC,ADAB=23,DE=4cm,则BC的长为( )
A. 6cm
B. 8cm
C. 10cm
D. 12cm
7.不等式组x≥ax≤b有解,则( )
A. a>bB. a≥bC. a
A. 球B. 圆柱C. 圆锥D. 棱锥
9.按一定规律排列的单项式:2x3,3x5,4x7,5x9,6x11,7x13⋯⋯第n(n≥1,n为正整数)个单项式是( )
A. nxn+1B. nx2n+1C. (n+1)x2n−1D. (n+1)x2n+1
10.为切实落实“双减”,丰富课后服务活动形式,某校开展学生的绘画、书法、散文诗等艺术作品征集活动,从八年级5个班收集到的作品数量(单位:件)分别为50、45、42、46、50,则这组数据的中位数是( )
A. 46B. 45C. 50D. 42
11.某化肥厂第一季度生产了m肥,后每季度比上一季度多生产x%,第三季度生产的化肥为n,则可列方程为( )
A. m(1+x2)=nB. m(1+x%)2=n
C. (1+x%)2=nD. m+m(x%)2=n
12.2023年10月8日晚,伴随圣火缓缓熄灭,杭州第19届亚运会圆满闭幕,亚运是体育盛会,也是文化旅游的盛会,下列与杭州亚运会有关的图案中,属于中心对称图形的是( )
A. B.
C. D.
13.如图,在△ABC中,∠A=30°,∠ACB=90°,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则图中阴影部分的面积是( )
A. 8 3−4πB. 8 3−2πC. 16 3−8πD. 16 3−4π
14.若二次根式 2x−6在实数范围内有意义,则x的取值范围是( )
A. x≤3B. x>3C. x≥3D. x>−3
15.如图,正方形ABCD被两条与边平行的线段EF,GH分割成四个小矩形,EF与GH交于点P,连接GF.若正方形ABCD的边长与Rt△GBF的周长均为a,则矩形EPHD的面积是( )
A. 23a2B. 12a2C. 22a2D. 不能确定
第Ⅱ卷
二、填空题(本大题共4个小题,每小题2分,共8分)
16.一种商品每件盈利为a元,售出60件,共盈利______元(用含a的式子表示).
17.分解因式:2a2−2= ______.
18.学校为了解本校初一年级学生上学的交通方式,随机抽取了本校20名初一学生进行调查,其中有2名学生是乘私家车上学,如图是收集数据后绘制的扇形图.如果该校初一年级有640名学生,那么骑自行车上学的学生大约有______.
19.如图,在边长为2的正六边形ABCDEF中,点M,N分别是AF,CD的中点,连接BN,CM,BN与CM相交于点P,则BPPN的值为______.
三、解答题(本大题共8个小题,共62分.解答应写出文字说明,证明过程或演算步骤)
20.(本小题7分)
计算:(18)−23−(2024−π)0+ 20+4 5−3.
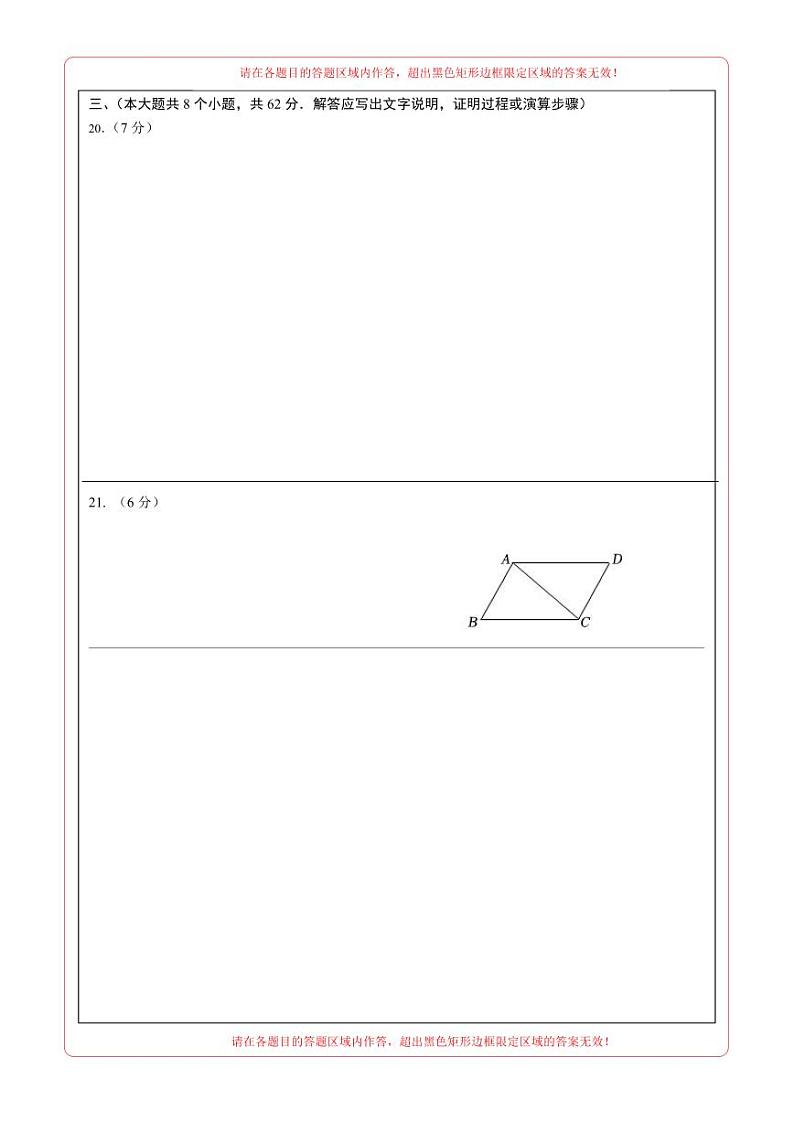
21.(本小题6分)
已知:如图,AD//CB,AD=CB.求证:∠ABC=∠CDA.
22.(本小题7分)
4月23日是“世界读书日”,某学校为开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,去年购进一批图书.经了解,科普书的单价比文学书的单价贵12元,用12000元购进的科普书本数是用9000元购进的文学书本数的45.那么文学书和科普书的单价各是多少元?
23.(本小题6分)
为了解全校1500名学生对篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
(1)乒乓球所对扇形的圆周角度数______.这次共抽取了______名学生进行调查,并补全条形图.
(2)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
24.(本小题8分)
某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)30≤x<60存在一次函数关系,部分数据如下表所示:
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
25.(本小题8分)
如图,AD//BE,AC平分∠BAD,且交BE于点C.
(1)作∠ABE的角平分线交AD于点F(要求:尺规作图,不写作法和结论,保留作图痕迹);
(2)根据(1)中作图,连接CF,求证:四边形ABCF是菱形.
26.(本小题8分)
如图,抛物线y=ax2+bx+3与x轴交于A(−3,0),B(1,0)两点.交y轴于点C.
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,使得S△PBC=12S△ABC,若存在,请直接写出点P的坐标;若不存在,请说明理由.
27.(本小题12分)
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC//BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=34,CD=24,求⊙O的半径;
(3)请问GF2−GB2 2DF⋅GF的值为定值吗?若是,请写出计算过程,若不是,请说明理由.
在物理学中,把物体所受的压力与受力面积的比叫做压强(pressure).
压强的计算公式为P=FS
P:压强
F:压力
S:受力面积
销售价格x(元/千克)
50
40
日销售量y(千克)
100
200
2024年云南省盘龙区中考一模考试数学试题: 这是一份2024年云南省盘龙区中考一模考试数学试题,共10页。试卷主要包含了本卷为试题卷,估计实数的值应在,下列运算正确的是,若分式有意义,则x的取值范围是等内容,欢迎下载使用。
2024年云南省红河州+中考一模考试数学试题卷: 这是一份2024年云南省红河州+中考一模考试数学试题卷,共4页。
2023年云南省文山州中考数学二模试卷-普通用卷: 这是一份2023年云南省文山州中考数学二模试卷-普通用卷,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












