中考数学（南通卷）-2024年中考数学第三次模考试

这是一份中考数学（南通卷）-2024年中考数学第三次模考试，文件包含数学南通卷全解全析docx、数学南通卷参考答案及评分标准docx、数学南通卷考试版A4docx、数学南通卷考试版A3docx、数学南通卷答题卡pdf等5份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。

2、二模考试大致在五月份，难度相对较大。这次考试主要检测学校以及学生在第一轮复习的成果，让老师和孩子找到问题的关键，是否存在基础不扎实，计算能力是否需要加强等等。然后找到解决方法，做到复习方法的改进，以及重难点的分布，复习的目标。
3、三模考试大概在中考前两周左右，三模是中考前的最后一次考前检验。三模学校会有意降低难度，目的是增强考生信心，难度只能是中上水平，主要也是对初中三年的知识做一个系统的检测，让学生知道中考的一个大致体系和结构。
2024年中考第三次模拟考试（南通卷）
数 学
（考试时间：120分钟 试卷满分：150分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．分式有意义，则的取值范围是（ ）
A．全体实数B．C．D．
2．下列各式中，计算正确的是（ ）
A．B．
C．D．
3．如图，在数轴上A、B两点分别对应数轴a、b，则下列结论中正确的是（ ）
A．B．C．D．
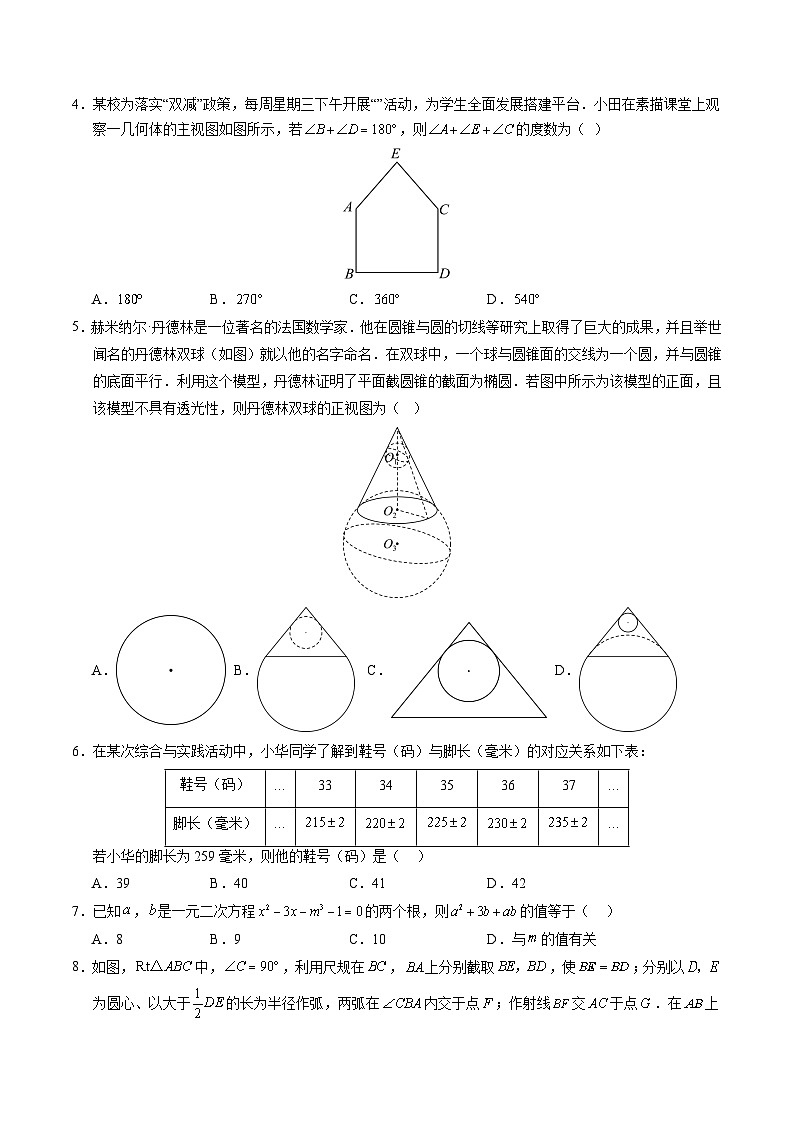
4．某校为落实“双减”政策，每周星期三下午开展“”活动，为学生全面发展搭建平台．小田在素描课堂上观察一几何体的主视图如图所示，若，则的度数为（ ）
A．B．C．D．
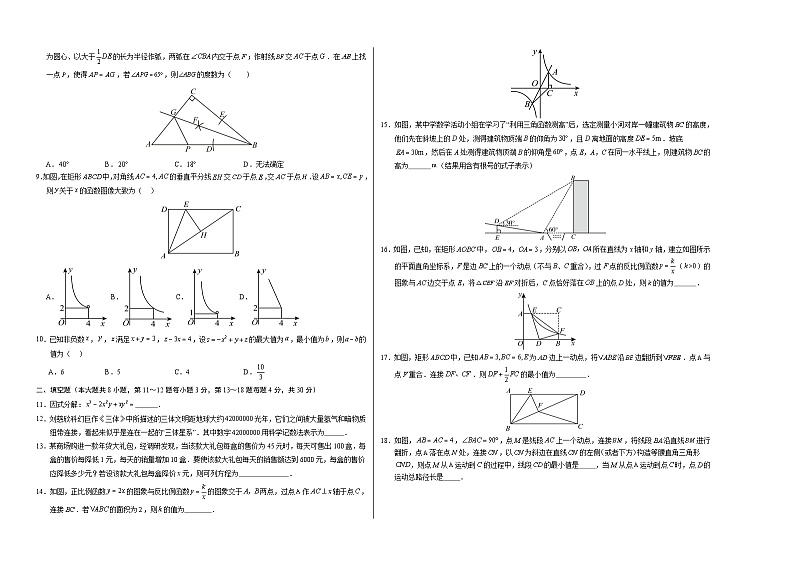
5．赫米纳尔·丹德林是一位著名的法国数学家．他在圆锥与圆的切线等研究上取得了巨大的成果，并且举世闻名的丹德林双球（如图）就以他的名字命名．在双球中，一个球与圆锥面的交线为一个圆，并与圆锥的底面平行．利用这个模型，丹德林证明了平面截圆锥的截面为椭圆．若图中所示为该模型的正面，且该模型不具有透光性，则丹德林双球的正视图为（ ）
A． B． C． D．
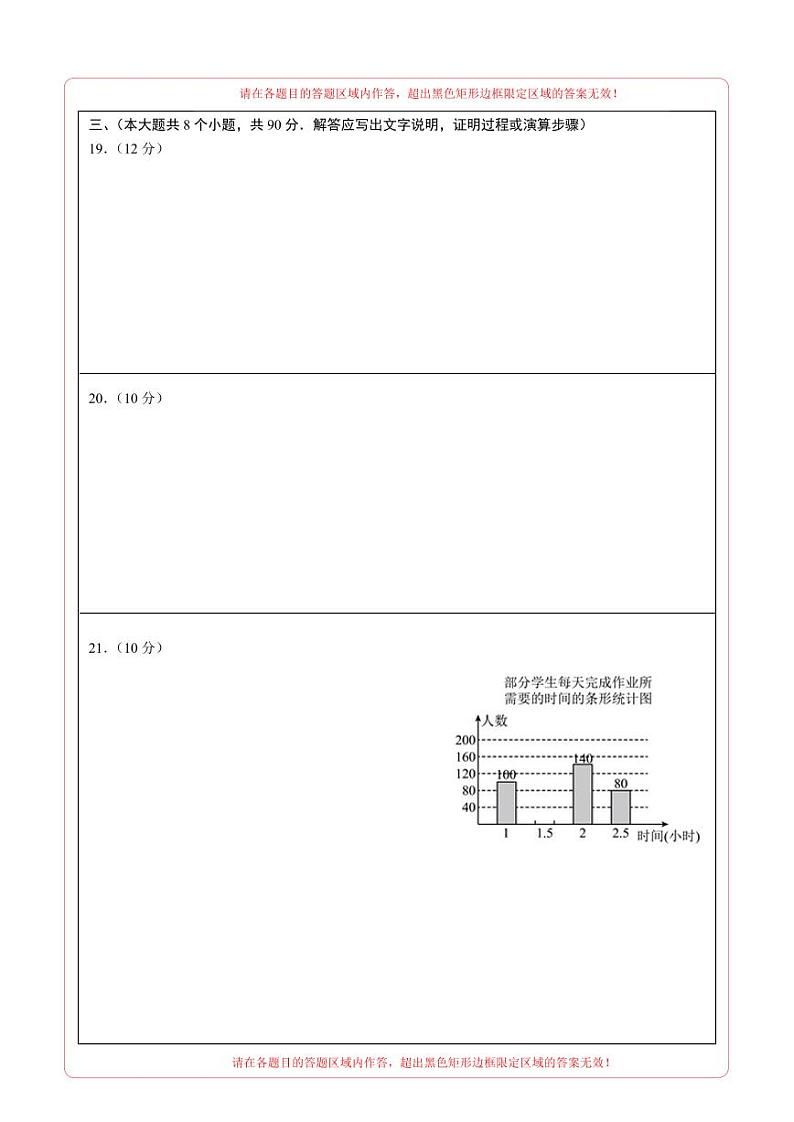
6．在某次综合与实践活动中，小华同学了解到鞋号（码）与脚长（毫米）的对应关系如下表：
若小华的脚长为259毫米，则他的鞋号（码）是（ ）
A．39B．40C．41D．42
7．已知，是一元二次方程的两个根，则的值等于（ ）
A．8B．9C．10D．与的值有关
8．如图，中，，利用尺规在，上分别截取，使；分别以为圆心、以大于的长为半径作弧，两弧在内交于点；作射线交于点．在上找一点，使得，若，则的度数为（ ）
A．B．C．D．无法确定
9．如图，在矩形中，对角线的垂直平分线交于点，交于点．设，则关于的函数图像大致为（ ）
A． B． C． D．
10．已知非负数，，满足，，设的最大值为，最小值为，则的值为（ ）
A．6B．5C．4D．
二、填空题（本大题共8小题，第11～12题每小题3分，第13～18题每题4分，共30分）
11．因式分解： ．
12．刘慈欣科幻巨作《三体》中所描述的三体文明距地球大约光年，它们之间被大量氢气和暗物质纽带连接，看起来似乎是连在一起的“三体星系”．其中数字用科学记数法表示为 ．
13．某商场购进一款年货大礼包，经调研发现，当该款大礼包每盒的售价为45元时，每天可售出100盒．每盒的售价每降低1元，每天的销量增加10盒．要使该款大礼包每天的销售额达到6000元，每盒的售价应降低多少元？若设该款大礼包每盒降价x元，则可列方程为 ．
14．如图，正比例函数的图象与反比例函数的图象交于两点，过点作轴于点，连接．若的面积为，则的值为 ．
15．如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为，且D离地面的高度．坡底，然后在A处测得建筑物顶端B的仰角是，点E，A，C在同一水平线上，则建筑物的高为 （结果用含有根号的式子表示）
16．如图，已知，在矩形中，，分别以所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边上的一个动点（不与B、C重合），过F点的反比例函数（）的图象与边交于点E，将沿对折后，C点恰好落在上的点D处，则k的值为 ．
17．如图，矩形中，已知为边上一动点，将沿边翻折到．点与点重合．连接．则的最小值为 ．
18．如图，，，点是线段上一个动点，连接，将线段沿直线进行翻折，点落在点处，连接，以为斜边在直线的左侧或者下方构造等腰直角三角形，则点从运动到的过程中，线段的最小值是 ，当从点运动到点时，点的运动总路径长是 ．
三、解答题（本大题共8个小题，共90分．解答应写出文字说明，证明过程或演算步骤）
19．（12分）计算：
(1)不等式组的解集；
(2)计算：．
20．（10分）随着社会经济发展和物质消费水平的大幅度提高，我国每年垃圾产生量迅速增长，为了倡导绿色社区，做好垃圾分类工作，某社区成立了甲、乙两个检查组，采取随机抽查的方式对辖区内四个小区进行抽查，并且每个小区不重复检查．
(1)若由甲组对四个小区进行抽查，则抽到B小区的概率是________；
(2)若甲、乙两组同时抽查，请用画树状图法或列表法求出甲组抽到C小区，同时乙组抽到D小区的概率．
21．（10分）近期教育部表示 “双减”依然是今年工作中的“重中之重”，作为“双减”政策落地后第二个学期，不少学校的作业总量已经大幅减少．依据政策要求，初中书面作业平均完成时间不超过分钟，学生每天完成作业的时长不能超过小时．某中学自纠自查，对本校学生的作业情况进行了抽样调查，统计结果如图所示：
(1)这次抽样共调查了 名学生，并补全条形统计图；
(2)计算扇形统计图中表示作业时长为小时对应的扇形圆心角度数为 ；
(3)若该中学共有学生人，请据此估计该校学生的作业时间不少于小时的学生人数；
(4)通过本次调查，你认为该学校作业布置是否满足教育部的“双减”政策要求？请说明理由．
22．（10分）如图，是的外接圆，为的直径，点为弧中点，连接，作的平分线交于点，连接．
(1)求证：；
(2)若过C点的切线与的延长线交于点F，已知，求弧、线段围成的阴影部分面积．
23．（10分）问题情境：如图①，一只蚂蚁在一个长为，宽为的长方形地毯上爬行，地毯上堆放着一根正三棱柱的木块，它的侧棱平行且等于宽，木块从正面看是一个边长为的等边三角形，求一只蚂蚁从点A处到达点C处需要走的最短路程．
(1)数学抽象：将蚂蚁爬行过的木块的侧面“拉直”“铺平”，“化曲为直”，请在图②中用虚线补全木块的侧面展开图，并用实线连接；
(2)线段的长即蚂蚁从点A处到达点C处需要走的最短路程，依据是_________；
(3)问题解决：求出这只蚂蚁从点A处到达点C处需要走的最短路程．
24．（12分）如图是一个东西走向近似于抛物线的山坡，以地面的东西方向为轴，西侧的坡底为原点建立平面直角坐标系，山坡近似满足函数解析式，无人机从西侧距坡底为10米处的点起飞，沿山坡由西向东飞行，飞行轨迹可以近似满足抛物线．当无人机飞越坡底上空时（即点），与地面的距离为20米．
(1)求无人机飞行轨迹的函数解析式；
(2)当无人机飞行的水平距离距起点为30米时，求无人机与山坡的竖直距离；
(3)由于山坡上有障碍物，无人机不能离山坡过近．当无人机与山坡的竖直距离大于9米时，无人机飞行才是安全的，请判断无人机此次飞行是否安全，并说明理由．
25．（13分）问题情境：数学活动课上，王老师给同学们每人发了一张矩形纸片探究折叠的性质在矩形的边上取一点，将沿翻折，使点恰好落在边上点处．
实践探究：（1）如图1，若，求的度数；
（2）如图2，当，且时，求的长；
问题解决：（3）如图3，延长，与的角平分线交于点，交于点，当时，求的值．
26．（13分）对某一个函数给出如下定义：如果函数的自变量与函数值满足：当时，（为实数，且，我们称这个函数在上是“民主函数”．比如：函数在上是“民主函数”．理由：由，得．，，解得，，是“民主函数”．
(1)反比例函数是上的“民主函数”吗？请判断并说明理由：
(2)若一次函数在上是“民主函数”，求此函数的解析式（可用含的代数式表示）；
(3)若抛物线在上是“民主函数”，且在上的最小值为，设抛物线与直线交于点，与轴相交于点．若的内心为，外心为，试求的长．
鞋号（码）
…
33
34
35
36
37
…
脚长（毫米）
…
…