2024年广东省汕头市濠江区中考二模数学试题(无答案)

这是一份2024年广东省汕头市濠江区中考二模数学试题(无答案)，共6页。试卷主要包含了解答题等内容，欢迎下载使用。
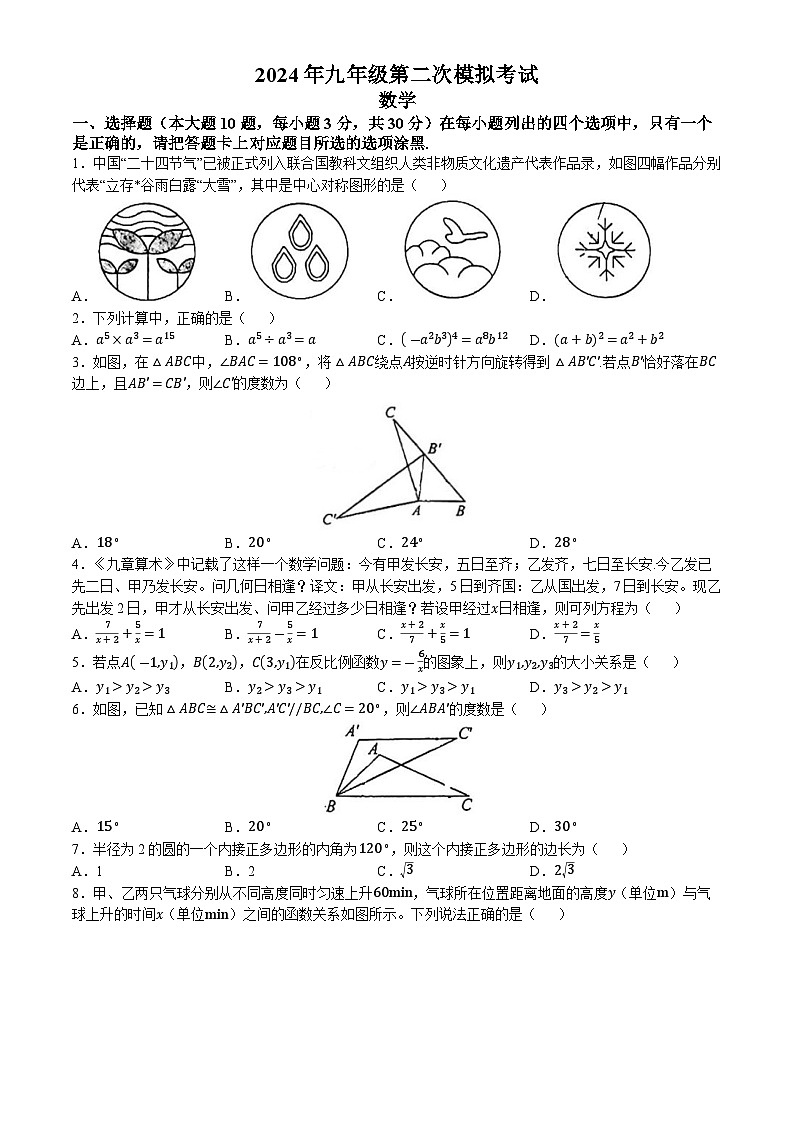
一、选择题（本大题10题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.
1．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，如图四幅作品分别代表“立存*谷雨白露“大雪”，其中是中心对称图形的是（ ）
A．B．C．D．
2．下列计算中，正确的是（ ）
A．a​5×a​3=a​15B．a​5÷a​3=aC．-a​2b​3​4=a​8b​12D．a+b​2=a​2+b​2
3．如图，在△ABC中，∠BAC=108​∘，将△ABC绕点A按逆时针方向旋转得到△AB​'C​'.若点B'恰好落在BC边上，且AB​'=CB​'，则∠C​'的度数为（ ）
A．18​∘B．20​∘C．24​∘D．28​∘
4．《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安.今乙发已先二日、甲乃发长安。问几何日相逢？译文：甲从长安出发，5日到齐国：乙从国出发，7日到长安。现乙先出发2日，甲才从长安出发、问甲乙经过多少日相逢？若设甲经过x日相逢，则可列方程为（ ）
A．7x+2+5x=1B．7x+2-5x=1C．x+27+x5=1D．x+27=x5
5．若点A-1,y1，B2,y2，C3,y1在反比例函数y=-6x的图象上，则y1,y2,y3的大小关系是（ ）
A．y1>y2>y3B．y2>y3>y1C．y1>y3>y1D．y3>y2>y1
6．如图，已知△ABC≅△A​'BC​',A​'C​'//BC,∠C=20​∘，则∠ABA​'的度数是（ ）
A．15​∘B．20​∘C．25​∘D．30​∘
7．半径为2的圆的一个内接正多边形的内角为120​∘，则这个内接正多边形的边长为（ ）
A．1B．2C．3D．23
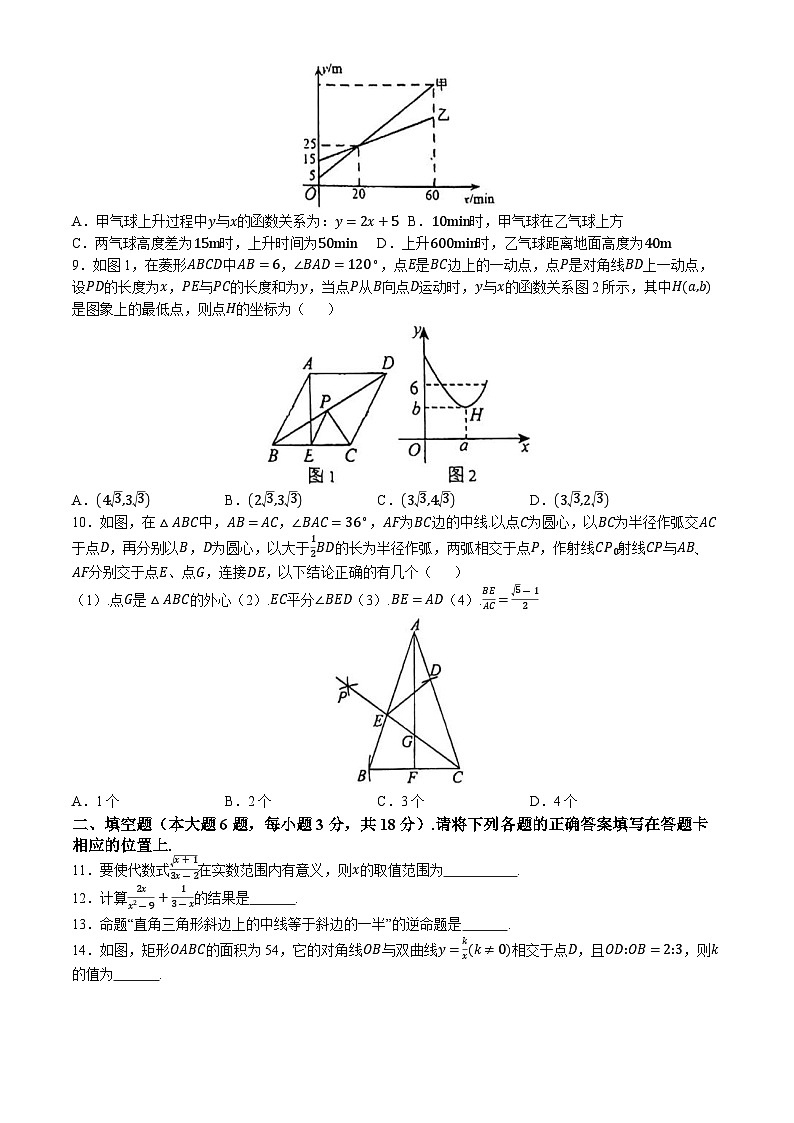
8．甲、乙两只气球分别从不同高度同时匀速上升60min，气球所在位置距离地面的高度y（单位m）与气球上升的时间x（单位min）之间的函数关系如图所示。下列说法正确的是（ ）
A．甲气球上升过程中y与x的函数关系为：y=2x+5B．10min时，甲气球在乙气球上方
C．两气球高度差为15m时，上升时间为50minD．上升600min时，乙气球距离地面高度为40m
9．如图1，在菱形ABCD中AB=6，∠BAD=120​∘，点E是BC边上的一动点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，当点P从B向点D运动时，y与x的函数关系图2所示，其中Ha,b是图象上的最低点，则点H的坐标为（ ）
A．43,33B．23,33C．33,43D．33,23
10．如图，在△ABC中，AB=AC，∠BAC=36​∘，AF为BC边的中线.以点C为圆心，以BC为半径作弧交AC于点D，再分别以B，D为圆心，以大于12BD的长为半径作弧，两弧相交于点P，作射线CP0射线CP与AB、AF分别交于点E、点G，连接DE，以下结论正确的有几个（ ）
（1）.点G是△ABC的外心（2）.EC平分∠BED（3）.BE=AD（4）.BEAC=5-12
A．1个B．2个C．3个D．4个
二、填空题（本大题6题，每小题3分，共18分）.请将下列各题的正确答案填写在答题卡相应的位置上.
11．要使代数式x+13x-2在实数范围内有意义，则x的取值范围为 .
12．计算2xx​2-9+13-x的结果是 .
13．命题“直角三角形斜边上的中线等于斜边的一半”的逆命题是 .
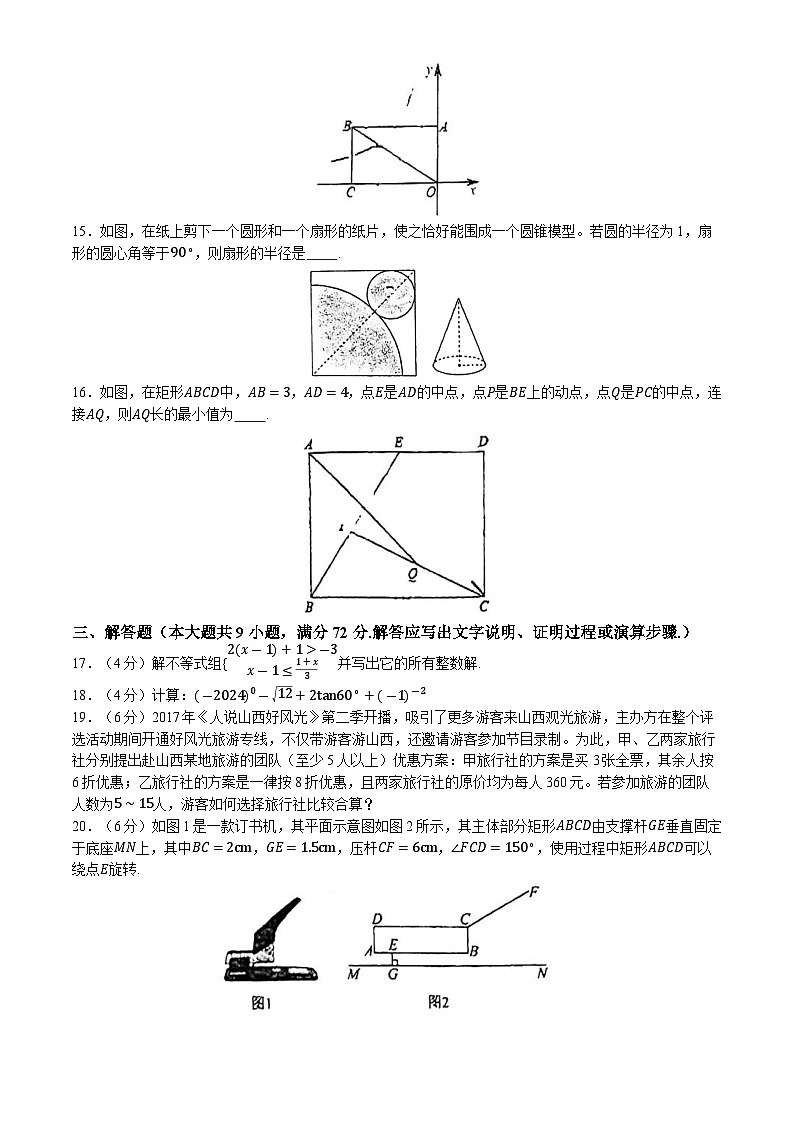
14．如图，矩形OABC的面积为54，它的对角线OB与双曲线y=kxk≠0相交于点D，且OD:OB=2:3，则k的值为 .
15．如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型。若圆的半径为1，扇形的圆心角等于90​∘，则扇形的半径是 .
16．如图，在矩形ABCD中，AB=3，AD=4，点E是AD的中点，点P是BE上的动点，点Q是PC的中点，连接AQ，则AQ长的最小值为 .
三、解答题（本大题共9小题，满分72分.解答应写出文字说明、证明过程或演算步骤.）
17．（4分）解不等式组{2x-1+1>-3x-1≤1+x3并写出它的所有整数解.
18．（4分）计算：-20240-12+2tan60∘+-1-2
19．（6分）2017年《人说山西好风光》第二季开播，吸引了更多游客来山西观光旅游，主办方在整个评选活动期间开通好风光旅游专线，不仅带游客游山西，还邀请游客参加节目录制。为此，甲、乙两家旅行社分别提出赴山西某地旅游的团队（至少5人以上）优惠方案：甲旅行社的方案是买3张全票，其余人按6折优惠；乙旅行社的方案是一律按8折优惠，且两家旅行社的原价均为每人360元。若参加旅游的团队人数为5∼15人，游客如何选择旅行社比较合算？
20．（6分）如图1是一款订书机，其平面示意图如图2所示，其主体部分矩形ABCD由支撑杆GE垂直固定于底座MN上，其中BC=2cm，GE=1.5cm，压杆CF=6cm，∠FCD=150​∘，使用过程中矩形ABCD可以绕点E旋转.
（1）订书机不使用时，如图2，AB//MN，求压杆端点F到底座MN的距离；
（2）使用过程中，当点B落在底座MN上时，如图3，测得∠GBE=15​∘，求压杆端点F到底座MN的高度.
（参考数据：sin15∘=0.26，cs15∘≈0.97，结果精确到0.1cm）
21．（8分）第41届潍坊国际风筝会来临之际，某商铺打算购进甲，乙两种风筝的文创产品向游客销售.已知甲种的进价比乙种的进价每件多1元，用1600元采购甲种的件数是用720元采购乙种的件数的2倍，两种文创产品的售价均为每件15元.
（1）求甲、乙两种文创产品每件的进价分别为多少元？
（2）商铺计划采购这两种文创产品共800件，采购乙种的件数不低于490件，但不超过甲种件数的4倍。厂家给出的优惠方案是：若一次性采购甲种超过180件时，甲种超过的部分按原进价打6折。设这次购买甲种文创产品的件数为x件，售出甲、乙两种产品所获的总利润为w元，请写出w与x的函数关系式，并求出这次采购的文创产品的最大利润.
22．（10分）如图，AB为⊙O的直径，点C在⊙O上.
（1）尺规作图：求作BC⌢的中点D（保留作图痕迹，不写作法）；
（2）过点D作DE⊥AC交AC延长线于点E（画出图形即可，不必尺规作图），求证：ED与⊙O相切；
（3）连接EO，若DE=2CE，求EOAO的值.
23．（10分）如图，矩形ABCD中，AC为对角线，将△ABC以点B为中心逆时针旋转，点C的对应点E在AD边上，点A的对应点为F点，连接FC交BE于点P.
（1）若∠ECD=20​∘，求∠AEB的度数；
（2）求证：P为FC的中点；
（3）若FC=2EC=26，求矩形ABCD的周长.
24．（12分）【问题初探】
（1）如图1，△ABC中，AB=AC，∠BAC=90​∘，点E在线段BC上，BD⊥AE，垂足为点D，连接CD，∠ADC=60​∘，求证：AD-BD=12CD；
丽丽和东东两名同学从不同角度进行思考，给出了两种解题思路。
①如图2，丽丽从条件出发，发现∠DAC-∠ABD，利用条件AB=AC，结合“边角边“定理在AD边上截取AF=BD，构造了一对全等三角形，将求证的问题转化为CD与DF的数量关系.
②如图3，东东受到丽丽的启发，也利用“边角边”定理，在BD的延长线上取点F，使BF=AD，连接AF，得到了△ADC≅△BFA，发现∠AFD=60​∘，利用边角之间的关系证明了问题.
请你选择一名同学的解题思路，写出解答过程，也可以用不同于上面两位同学的方法进行解答.
【迁移应用】
（2）如图4，在△ABC中，∠BAC=90​∘，AB=AC，点E在线段BC上，过点B作BD⊥AB，交AE的延长线于点D，线段AD绕点D逆时针旋转90​∘得到线段DF，当点F恰好在CB的延长线时，求证BF=2BD.
【能力提升】
（3）在（2）的条件下，若AB=4，请直接写出△BDE的面积.
25．（12分）在平面直角坐标系xOy中，已知抛物线y=ax​2-3ax+c与x轴分别交于A-1,0，B两点，与y轴交于点C0,-2.
（1）求抛物线的函数表达式；
（2）如图1，点D为第四象限抛物线上一点，连接AD,BC交于点E，求DEAE的最大值；
（3）如图2，连接AC,BC，过点O作直线l//BC，点P,Q分别为直线l和抛物线上的点，试探究：在第一象限是否存在这样的点P,Q，使△PQB∽△CAB，若存在，请写出所有符合条件的点P的坐标；若不存在，请说明理由.