北师大版 (2019)必修 第一册2 数学建模的主要步骤说课课件ppt

这是一份北师大版 (2019)必修 第一册2 数学建模的主要步骤说课课件ppt，共12页。PPT课件主要包含了内容要求，探究新知，基本过程，思考交流等内容，欢迎下载使用。

数学建模活动是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的过程.主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、构建模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题.数学建模活动是基于数学思维运用模型解决实际问题的一类综合实践活动，是高中阶段数学课程的重要内容.
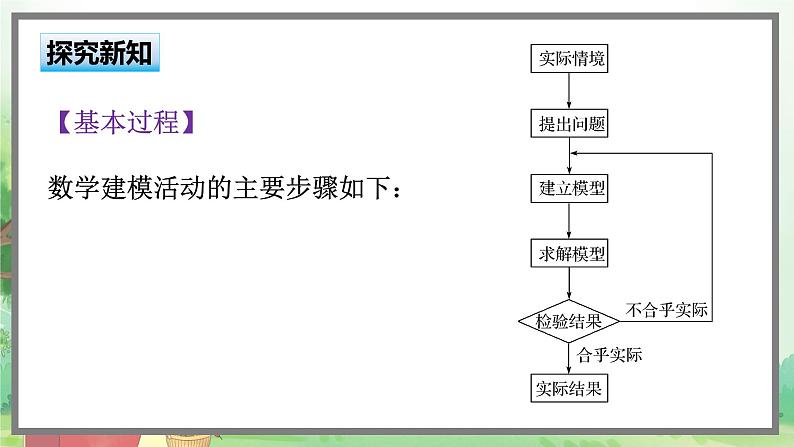
数学建模活动的主要步骤如下：
在一个十字路口，每次亮绿灯的时长为15s，那么，每次绿灯亮时，在一条直行道路上能有多少汽车通过十字路口？
这个问题涉及车长、车距、车速、堵塞的干扰等多种因素.而不同型号车的车长是不同的,驾驶员的习惯不同也会使车距、车速不同,行人和非机动车的干扰因素则复杂且不确定.面对这些不同和不确定,就需要作出假设.例如，虽然通过路口的车辆各种各样,但多数是小轿车，因此这次建模就只考虑小轿车的情况，它们的长度差距不大,可以假设车辆长度都相同.
经过对相关因素的分析，可以作出有利于建立模型、基本符合实际情况的几个假设：（1）通过路口的车辆长度都相等；（2）等待时，前后相邻两辆车的车距都相等；（3）绿灯亮后，汽车都是在静止状态下匀加速启动；（4）前一辆车启动后，下一辆车启动的延时时间相等；（5）车辆行驶秩序良好，不会发生堵塞.
用Sn(t)表示时刻t第n辆汽车所在的位置，停车线位置记作0，则Sn(0)=-(n-1)(l+d).这样，实际问题就可以表述为数学问题：求满足Sn(15)>0的n的最大值，其中
【求解模型】 代入各个量的参数值，可以计算出绿灯亮至15s时若干辆汽车的位置，如表：
由表可见，绿灯亮至15s时，第7辆车已经驶过停车线16.0m，而第8辆车还距停车线2.1m，没有通过.因此，15s的绿灯最多可以通过7辆汽车。
【检验结果】 到十字路口实地调查，对结论做检验.若没有明显误差，就可以使用这个模型.否则，再修改假设，重新建模.
1.从小学到中学,在数学学习中,做过不少“应用题”,比较上述实际问题的解决,说明用数学建模的方法解决实际问题和做应用题有什么联系和区别。2.总结数学建模的基本步骤.
数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的过程.主要过程包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确立参数、求解模型,检验结果、改进模型,最终解决实际问题.