高中SJ数学选择性必修第一册 2.4 回顾与检测 PPT课件

这是一份高中SJ数学选择性必修第一册 2.4 回顾与检测 PPT课件，共35页。
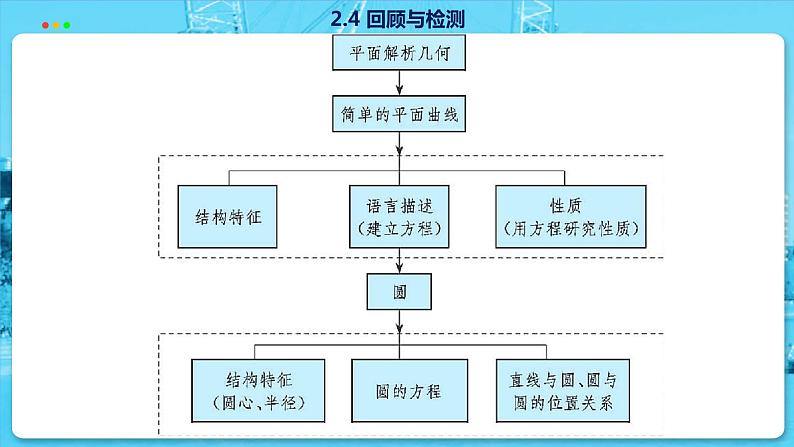
第2章 圆与方程苏教数学选择性必修第一册本章回顾2.4 回顾与检测本章概览本章再一次借助平面直角坐标系，运用坐标法，研究了圆的有关知识，学习本章时，应该进一步体会用坐标法研究问题的一般思路和基本方法，也就是在明确了圆的定义，即圆上的点到圆心的距离为定值后，通过建立直角坐标系，将圆转化为方程，进而通过圆的方程等代数方法来研究点与圆、直线与圆、圆与圆之间的位置关系,本章以圆为载体，再一次展示了坐标法这一研究几何曲线的重要数学方法，即通过坐标系，把圆与方程联系起来，沟通了圆与方程之间的联系，体现了数形结合的重要数学思想.圆的标准方程和一般方程都含有三个参变量 (标准方程中为 a，b，r；一般方程中为 D，E，F)，也就是说，从解方程的角度看，要确定一个圆的方程，需要三个独立的条件，这与不共线的三点确定一个圆是一致的.复习题2.4 回顾与检测感受·理解1. 已知圆经过点 P(1，1) 和坐标原点，且圆心在直线 2x＋3y＋1＝0 上，求圆的方程.答案：(x－4)2＋(y＋3)2＝25.2. 已知圆经过三点 A(1，12)，B(7，10)，C(－9，2)，求圆的方程.答案：x2＋y2－2x－4y－95＝0.3. 已知直线 3x－4y＋12＝0 与两坐标轴分别交于点 A，B，求以线段 AB为直径的圆的方程. 4. 求圆 x2＋y2－4x＋4y＋4＝0 被直线 x－y－5＝0 所截得的弦长. 5. 已知一直线与圆 C：x2＋(y＋5)2＝3 相切，且在 x 轴、y 轴上的截距相等，求此直线的方程.   7. 判断两个圆 x2＋y2＋x－2y－20＝0 与 x2＋y2＝25 的位置关系.答案：相交.8. 若一个圆过点 P(4，－1)，且与圆 C：x2＋y2＋2x－6y＋5＝0 相切于点 M (1，2)，求此圆的方程.答案：(x－3)2＋ (y－1)2＝5.9. 河北省赵县的赵州桥，是世界上现存最古老的石拱桥之一. 赵州桥的跨度约为 37.4m，圆拱高约为7.2m，试建立适当的直角坐标系，求出这个圆拱所在的圆的方程.答案：x2＋(y＋20.7)2＝27.92.10. 已知圆 O：x2＋y2＝1 和定点 A(4，0)，P为圆O外一点，直线 PQ 与圆O 相切于点Q. 若 PQ＝2PA，求点 P 的轨迹方程. 思考·运用11. 已知 M(1，0) 是圆 C：x2＋y2－4x－2y＝0 内一点，求过点 M 的最短弦所在直线的方程.答案：x＋y－1＝0.  13. 光线沿直线 3x＋4y＋6＝0 射入，经过 x 轴反射后，反射光线与以点 (2，8)为圆心的圆 C 相切，求圆 C 的方程.答案：(x－2)2＋ (y－8)2＝16.14. 已知两圆 x2＋y2＝10 和 (x－1)2＋(y－3)2＝20 相交于 A，B 两点，求直线 AB 的方程.答案：x＋3y＝0.15.设 r 为正实数，若集合 M＝{(x，y)|x2＋y2≤4}，N＝{(x，y)|(x－1)2＋(y －1)2≤r2}. 当 M∩N＝N 时，求 r 的取值范围.   探究·拓展17. 已知圆 C：x2＋y2－2x＋4y－4＝0，是否存在斜率为 1 的直线 l，使以 l被圆 C 截得的弦 AB 为直径的圆过原点? 若存在，求出直线 l 的方程；若不存在，说明理由.答案： y＝x＋1 或 y＝x－4.18. 已知直线 l：x＝－2 和圆 C：(x－3)2＋y2＝1. 若圆 M 与直线 l 相切，与圆 C 外切，求圆 M 的圆心 M 的轨迹方程.答案： y2＝12x.本章测试第2章 圆与方程一、填空题1. 圆心为点(－1，1)，半径为 3 的圆的方程为 ______________________.2. 圆 x2＋y2－2x＋4y＝0 的面积为____________.3. 经过两点 (3，5) 和 (－3，7)，且圆心在 x 轴上的圆的方程为 _________ __________________.4. 圆 x2＋y2－2x＋2y＋1＝0 关于 x 轴对称的圆的方程为_______________.(x＋1)2＋(y－1)2＝95π(x＋2)2＋y2＝50x2＋y2－2x－2y＋1＝0 5.设 m 为实数，若方程 x2＋y2－2x＋4y＋m＝0 表示圆，则 m 的取值范围为____________.6. 圆 x2＋y2－2x－2y＋1＝0 上的点到直线 x－y＝2 的距离的最大值为 ___ _________.(－∞，5) 二、选择题7. 已知圆的内接正方形的一条对角线上的两个顶点的坐标分别是 (5，6)，(3，－4)，则这个圆的方程为( ).A. x2＋y2＋4x－2y＋7＝0B. x2＋y2－8x－2y－9＝0C. x2＋y2＋8x＋2y－6＝0D. x2＋y2－4x＋2y－5＝0B8. 过圆 x2＋y2＝5 上一点 M(1，－2) 作圆的切线，则 l 的方程为( ).A. x＋2y－3＝0 B. x－2y－5＝0C. 2x－y－5＝0 D. 2x＋y－5＝09. 圆 O1：x2＋y2－2x＝0 与圆 O2：x2＋y2＋4y＝0 的位置关系为( ).A.外离 B.外切 C.相交 D.内切BC D三、解答题11. 若圆 C 过两点 A(0，4)，B(4，6)，且圆心在直线 x－2y－2＝0 上，求圆 C 的标准方程.答案： (x－4)2＋(y－1)2＝25.  13. 若圆 C 的圆心在直线 3x＋2y＝0 上，且圆 C 与 x 轴的交点分别为 (－2，0)，(6，0)，求圆 C 的方程.答案：(x－2)2＋(y＋3)2＝25.14. 已知直线 l1：2x－y－3＝0，l2：x－2y＋3＝0，若圆 C 的圆心在 x 轴上且与直线 l1，l2 都相切，求圆 C 的方程. 15. 设 a 为实数，若直线 l 与圆 C：x2＋y2＋2x－4y＋a＝0 相交于 A，B 两点，弦 AB 的中点为 M(0，1)，求 a 的取值范围及直线 l 的方程.答案： x－y＋1＝0.