+安徽省阜阳市第十八中学2022-2023学年八年级下学期期末数学试卷+

这是一份+安徽省阜阳市第十八中学2022-2023学年八年级下学期期末数学试卷+，共16页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．（4分）点（3，-5）在正比例函数y=kx（k≠0）的图象上，则k的值为（ ）
A．﹣15B．15C．﹣D．﹣
2．（4分）若有意义，则a能取的最小整数为（ ）
A．0B．﹣4C．4D．﹣8
3．（4分）如果3，a，5是勾股数，则a的值是（ ）
A．4B．C．4或D．4或34
4．（4分）下列判断错误的是（ ）
A．两组对边分别相等的四边形是平行四边形
B．四个内角都相等的四边形是矩形
C．两条对角线互相垂直且相等的四边形是正方形
D．四条边都相等的四边形是菱形
5．（4分）一组数据：201、200、199、202、200，分别减去200，得到另一组数据：1、0、﹣1、2、0，其中判断错误的是（ ）
A．前一组数据的中位数是200
B．前一组数据的众数是200
C．后一组数据的平均数等于前一组数据的平均数减去200
D．后一组数据的方差等于前一组数据的方差减去200
6．（4分）已知正比例函数y=kx（k≠0）的图象如图所示，则一次函数y=k（1-x）的图象为（ ）
A．B．
C．D．
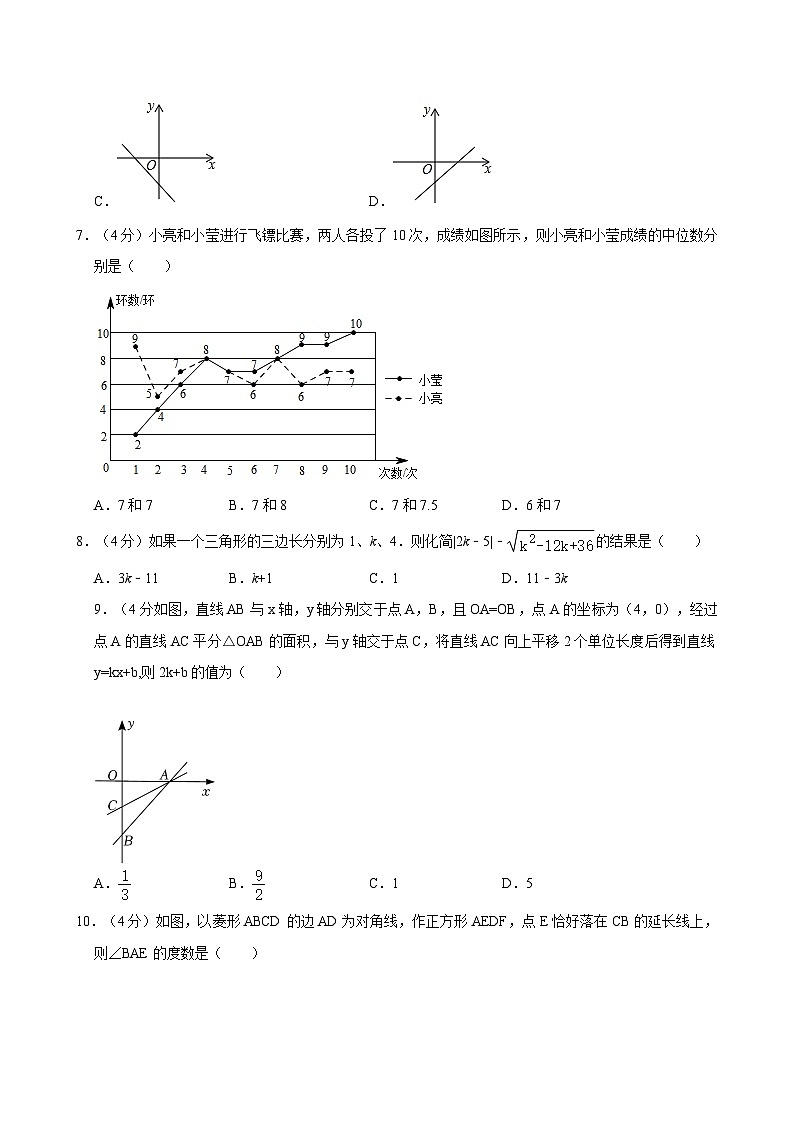
7．（4分）小亮和小莹进行飞镖比赛，两人各投了10次，成绩如图所示，则小亮和小莹成绩的中位数分别是（ ）
A．7和7B．7和8C．7和7.5D．6和7
8．（4分）如果一个三角形的三边长分别为1、k、4．则化简|2k﹣5|﹣的结果是（ ）
A．3k﹣11B．k+1C．1D．11﹣3k
9．（4分如图，直线AB与x轴，y轴分别交于点A，B，且OA=OB，点A的坐标为（4，0），经过点A的直线AC平分△OAB的面积，与y轴交于点C，将直线AC向上平移2个单位长度后得到直线y=kx+b,则2k+b的值为（ ）
A．B．C．1D．5
10．（4分）如图，以菱形ABCD的边AD为对角线，作正方形AEDF，点E恰好落在CB的延长线上，则∠BAE的度数是（ ）
A．10°B．15°C．20°D．25°
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）最简二次根式能与进行合并 ．
12．（5分）按照如图所示的计算程序，y与x之间的关系式为 ．
13．（5分）如图，将正方形OABC放在平面直角坐标系中，O为坐标原点，点A的坐标为（-3，1），则点B的坐标为 ．
14．（5分）如图，已知平行四边形ABCD中，AD=6，AB=，∠A=45°．过点B、D分别作BE⊥AD，DF⊥BC，交AD、BC与点E、F．点Q为DF边上一点，∠DEQ=30°，点P为EQ的中点，过点P作直线分别与AD、BC相交于点M、N．若MN=EQ，则EM的长等于 ．
三、（本大题共2小题，每小题8分，满分16分）
15．（8分）计算：．
16．（8分）如图，△ABC中，∠ACB=90°，D是AB中点，过点B作直线CD的垂线，垂足为E．求证：∠EBC=∠A．
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）如图，在矩形ABCD中（AB＜AD），BD为对角线．
（1）用尺规完成以下基本作图：作BD的垂直平分线分别交AD，BC于点E，F；（保留作图痕迹，不写作法）
（2）在（1）所作的图形中，若BC＝5，求BF的长．
18．（8分）已知一次函数y＝kx+b的图象经过点A（1，2），B（0，4）．
（1）求此函数的解析式．
（2）求原点到直线AB的距离．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）已知，，分别求下列代数式的值：
（1）a2﹣b2；
（2）a2﹣ab+b2．
20．（10分）如图．P是菱形ABCD的对角线AC上一点，PE⊥AB于点E，PF⊥AD于点F．
（1）若∠BAD=60°，PE=1，求AE的长；
（2）若∠BAD=90°，判断四边形AEPF的形状，并说明理由．
六、（本题满分12分）
21．（12分）在学校组织的知识竞赛中，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将八年级一班和二班的成绩整理并绘制成如下的统计图：
请你根据以上提供的信息解答下列问题：
（1）求一班参赛选手的平均成绩；
（2）此次竞赛中，二班成绩在C级以上（包括C级）的人数有几人？
（3）求二班参赛选手成绩的中位数．
七、（本题满分12分）
22．（12分）在一条笔直的公路上依次有A，C，B三地，甲、乙两人同时出发，甲从A地骑自行车去B地，途经C地休息1min,继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（m）与时间x（min）之间的函数关系如图所示，请结合图象解答下列问题：​
（1）请写出甲的骑行速度 m/min，点M的坐标 ．
（2）求甲返回时距A地的程y与时间x之间的函数解析式（不需要写出自变量的取值范围）．
（3）两人出发后，求经过多长时间两人相遇．
八、（本题满分14分）
23．（14分）如图，在平行四边形ABCD中，对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC=60°，，连结OE．
（1）求证：AB＝AE；
（2）若，求证：OE⊥AC；
（3）若，试求k与m满足的关系．
2022-2023学年安徽省阜阳十八中八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题4分，满分40分）
1．【答案】D
【解答】解：∵点（3，﹣5）在正比例函数y＝kx（k≠2）的图象上，
∴﹣5＝3k，
解得：k＝﹣，
故选：D．
2．【答案】B
【解答】解：有意义，则，
解得：a≥﹣8，
故a能取的最小整数为：﹣4．
故选：B．
3．【答案】A
【解答】解：∵3，a，5是勾股数，
∴a＝8，
故选：A．
4．【答案】C
【解答】解：A．两组对边分别相等的四边形是平行四边形，不符合题意；
B．四个内角都相等的四边形是矩形，不符合题意；
C．两条对角线互相垂直且相等的四边形不一定是正方形，符合题意；
D．四条边都相等的四边形是菱形，不符合题意；
故选：C．
5．【答案】D
【解答】解：A．前一组数据的中位数是200，此选项不符合题意；
B．前一组数据的众数是200，此选项不符合题意；
C．后一组数据的平均数等于前一组数据的平均数减去200，此选项不符合题意；
D．后一组数据的方差等于前一组数据的方差；
故选：D．
6．【答案】D
【解答】解：∵正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，
∴k＜0，
∵一次函数y＝k（3﹣x）的一次项系数大于0，常数项小于0，
∴一次函数y＝k（6﹣x）的图象经过第一、三象限．
故选：D．
7．【答案】C
【解答】解：小亮的成绩从小到大排列为：5，6，3，7，7，8，7，8，7，9；
故中位数为：（7+2）÷2＝7；
小莹的成绩从小到大排列为：6，4，6，8，7，8，3，9，9，10，
故中位数为：（3+8）÷2＝4.5；
故选：C．
8．【答案】A
【解答】解：∵三角形的三边长分别为1、k、4，
∴，
解得，3＜k＜5，
所以，5k﹣5＞0，
∴|6k﹣5|﹣＝6k﹣5﹣．
故选：A．
9．【答案】C
【解答】解：∵OA＝OB，点A的坐标为（4，
∴OA＝OB＝4，
∴S△OAB＝OA•OB＝8，
∵直线AC平分△OAB的面积，
∴S△OAC＝S△OAB＝4，
∴OA•OC＝4，即，
∴OC＝2，
∴C（5，﹣2），
设直线AC解析式为y＝mx﹣2，把A（7
0＝4m﹣7，
解得m＝，
∴直线AC解析式为y＝x﹣2，
∵将直线AC向上平移6个单位长度后得到直线y＝kx+b，
∴k＝，b＝5，
∴2k+b＝2×+0＝8，
故选：C．
10．【答案】B
【解答】解：如图，分别过E作EH⊥AD于H，
∵四边形AEDF为正方形，
∴∠AED＝90°，AE＝ED，
∴EH＝AD，
∵四边形ABCD为菱形，
∴AD∥BC，AD＝CD，
∴EH＝DG，
∴DG＝CD，
∴∠DCG＝30°＝∠DAB，
∴∠BAE＝∠EAD﹣∠DAB＝45°﹣30°＝15°．
故选：B．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．【答案】见试题解答内容
【解答】解：∵最简二次根式能与，
∴m+6＝3，
∴m＝2．
故答案为：6．
12．【答案】y＝﹣3x+2．
【解答】解：按照如图所示的计算程序，y与x之间的关系式为y＝﹣3x+2．
13．【答案】见试题解答内容
【解答】解：如图所示，过点A、y轴的垂线，
∠AEO＝∠BFA＝90°，∠AOE＝∠ABF，
∴△AEO≌△BFA，（AAS），
∴AF＝AE＝1，AG＝BF＝3，
BN＝AG﹣AF＝3﹣1＝2，
BM＝BF+AE＝6，
故点B坐标为（﹣2，4），
故答案为：（﹣7，4）．
14．【答案】见试题解答内容
【解答】解：如图，过点P作MN⊥EQ交AD于M，作NJ⊥AD于J．
在Rt△AEB中，∵∠AEB＝90°，
∴AE＝EB，
∵AB＝3，
∴AE＝EB＝8，
∵AD＝6，
∴AE＝ED＝3，
∵BE∥DF，DE∥BF，
∴四边形BFDE是平行四边形，
∵∠BED＝90°，
∴四边形BEDF是矩形，
∵BE＝DE＝5，
∴四边形BEDF是正方形，
易证△MNJ≌△QED（AAS），
∴MN＝EQ，
在Rt△EQD中，∵∠EDQ＝90°，
∴EQ＝＝2，
∵EP＝PQ＝，
∴EM＝＝2，
作PH⊥DE于H，作MN关于直线PH的对称直线M′N′，
易知HM＝HM′＝，
∴EM′＝2﹣1＝8，
综上所述，满足条件的EM的值为2或1．
故答案为7或2
三、（本大题共2小题，每小题8分，满分16分）
15．【答案】见试题解答内容
【解答】解：原式＝
＝
＝14．
16．【答案】见试题解答内容
【解答】解：∵∠ACB＝90°，D是AB中点，
∴CD＝BD，
∴∠ABC＝∠ECB，
∵BE⊥CE，
∴∠E＝90°，
∴∠ECB+∠CBE＝∠ABC+∠A＝90°，
∴∠EBC＝∠A．
四、（本大题共2小题，每小题8分，满分16分）
17．【答案】（1）见解答．
（2）．
【解答】解：（1）如图所示．
（2）连接DF，
∵EF为线段BD的垂直平分线，
∴BF＝DF，
∵四边形ABCD为矩形，
∴∠C＝90°，
设BF＝DF＝x，
则CF＝BC﹣BF＝5﹣x，
由勾股定理得，，
解得x＝，
∴BF的长为．
18．【答案】见试题解答内容
【解答】解：（1）把A（1，2），5）代入y＝kx+b得．
所以一次函数解析式为y＝﹣2x+4；
（2）由y＝﹣2x+4可知，直线与x轴的交点C的坐标为（6，
∴AC＝＝2，
设原点到直线AB的距离为h，
则•h•2＝，
解得h＝，
所以原点到直线AB的距离为．
五、（本大题共2小题，每小题10分，满分20分）
19．【答案】（1）8；
（2）13．
【解答】解：∵，，
∴a+b＝4，ab＝5﹣3＝1，
（1）a2﹣b2＝（a+b）（a﹣b）＝3×2＝4；
（2）a2﹣ab+b4＝（a+b）2﹣3ab＝72﹣3×8＝13．
20．【答案】（1）；
（2）四边形AEPF是正方形，理由见解析过程．
【解答】解：（1）∵四边形ABCD是菱形，
∴∠PAD＝∠PAB＝30°，
∵PE⊥AE，
∴AP＝2PE＝2，
∴AE＝＝＝；
（2）四边形AEPF是正方形，
理由如下：
在△APE和△APF中，
，
∴△APE≌△APF（AAS），
∴PE＝PF；
∵∠BAD＝90°，PE⊥AB，
∴四边形AEPF是矩形，
∴四边形AEPF是正方形．
六、（本题满分12分）
21．【答案】见试题解答内容
【解答】解：（1）一班参赛选手的平均成绩为＝88.5（分）；
（2）二班成绩在C级以上（包括C级）的人数有（5+10+3+3）×（1﹣25%）＝15（人）；
（3）∵C、D等级人数所占百分比为25%+30%＝55%＞50%，
∴中位数位于C等级，即二班参赛选手成绩的中位数为80分．
七、（本题满分12分）
22．【答案】（1）240，（6，1200）；
（2）y＝﹣240x+2640；
（3）4min或8min．
【解答】解：（1）甲的骑行速度为1020÷（﹣1）＝240（m/min）；
A、B两地的距离为240×（11﹣3）÷2＝1200（米），
∵甲往返的总时间为11min，途中休息1min，
∴点M的横坐标是11﹣（11﹣2）÷2＝6，
∴点M的坐标为（5，1200）．
故答案为：240，（6．
（2）设线段MN对应的函数关系式为y＝kx+b（k、b为常数．
将坐标M（6，1200）和N（11，
得，
解得，
∴甲返回时距A地的程y与时间x之间的函数解析式为y＝﹣240x+2640．
（3）由（1）可知，点D的坐标是（0．
设线段DE对应的函数关系式为y＝k3x+b1（k1、b7为常数，且k1≠0）．
将坐标D（8，1200）和E（201x+b1，
得，
解得，
∴线段DE对应的函数关系式为y＝﹣60x+1200（4≤x≤20）；
甲从A地到C地过程中y与x之间的函数关系式为y＝240x（0≤x≤）．
当甲从A地到C地的过程中与乙相遇时，得240x＝﹣60x+1200；
当甲从B地返回A地的过程中与乙相遇时，得﹣240x+2640＝﹣60x+1200；
综上，x＝5或8．
∴两人出发后，经过4min或7min两人相遇．
八、（本题满分14分）
23．【答案】（1）证明过程见解析；
（2）证明过程见解析；
（3）k+m＝2．
【解答】（1）证明：∵四边形ABCD为平行四边形，∠ADC＝60°，
∴∠ABC＝∠ADC＝60°，∠BAD＝120°，
∵AE平分∠BAD，
∴∠BAE＝∠DAE＝60°，
∴△ABE为等边三角形，
∴AB＝AE．
（2）证明：由（1）可知△ABE为等边三角形，即AB＝BE＝AE，
∵，
∴，
∴CE＝BC﹣BE＝2BE﹣BE＝BE，
∴AE＝CE，
∵O为平行四边形ABCD对角线的交点，
∴AO＝CO，
∴EO⊥AC（等腰三角形三线合一）．
（3）解：由平行四边形的性质可得：S△ABO＝S△BOC＝S△COD，
∵，
∴，
∵AE平分∠BAD，AD∥BC，
∴∠BAE＝∠DAE＝∠AEB，
∴AB＝BE＝mBC，
即EC＝BC﹣BE＝BC﹣mBC＝（4﹣m）BC，
∴，
得出k+m＝2．