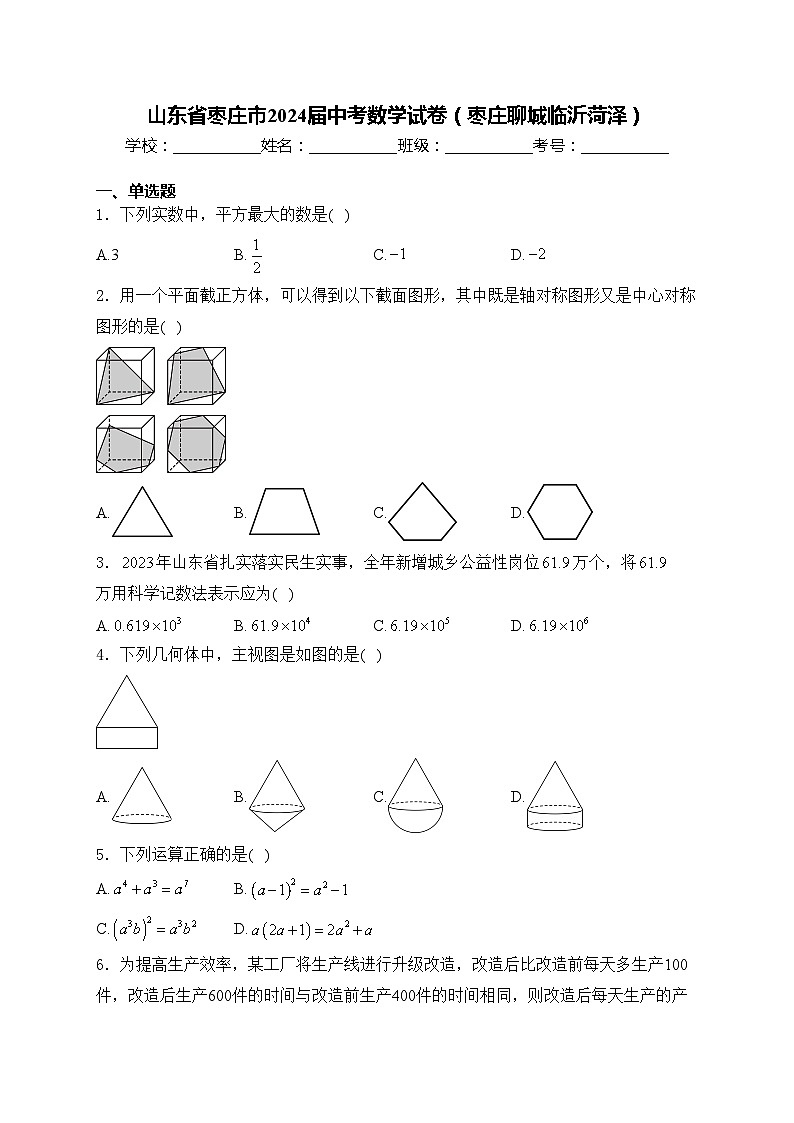
山东省枣庄市2024届中考数学试卷（枣庄聊城临沂菏泽）(含答案)

这是一份山东省枣庄市2024届中考数学试卷（枣庄聊城临沂菏泽）(含答案)，共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下列实数中，平方最大的数是( )
A.3B.C.D.
2．用一个平面截正方体，可以得到以下截面图形，其中既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
3．年山东省扎实落实民生实事，全年新增城乡公益性岗位万个，将万用科学记数法表示应为( )
A.B.C.D.
4．下列几何体中，主视图是如图的是( )
A.B.C.D.
5．下列运算正确的是( )
A.B.
C.D.
6．为提高生产效率，某工厂将生产线进行升级改造，改造后比改造前每天多生产100件，改造后生产600件的时间与改造前生产400件的时间相同，则改造后每天生产的产品件数为( )
A.200B.300C.400D.500
7．如图，已知，，是正n边形的三条边，在同一平面内，以为边在该正n边形的外部作正方形.若，则n的值为( )
A.12B.10C.8D.6
8．某校课外活动期间开展跳绳、踢毽子、韵律操三项活动，甲、乙两位同学各自任选其中一项参加，则他们选择同一项活动的概率是( )
A.B.C.D.
9．如图，点为的对角线上一点，，，连接并延长至点F，使得，连接，则为( )
A.B.3C.D.4
10．根据以下对话，
给出下列三个结论：
①1班学生的最高身高为；
②1班学生的最低身高小于；
③2班学生的最高身高大于或等于.
上述结论中，所有正确结论的序号是( )
A.①②B.①③C.②③D.①②③
二、填空题
11．因式分__________.
12．写出满足不等式组的一个整数解__________.
13．若关于x的方程有两个相等的实数根，则m的值为__________.
14．如图，是的内接三角形，若，，则__________.
15．如图，已知，以点A为圆心，以适当长为半径作弧，分别与、相交于点B，C；分别以B，C为圆心，以大于的长为半径作弧，两弧在内部相交于点P，作射线.分别以A，B为圆心，以大于的长为半径作弧，两弧相交于点D，E，作直线分别与，相交于点F，Q.若，，则F到的距离为__________.
16．任取一个正整数，若是奇数，就将该数乘3再加上1；若是偶数，就将该数除以2.反复进行上述两种运算，经过有限次运算后，必进入循环圈1→4→2→1，这就是“冰雹猜想”.在平面直角坐标系中，将点中的x，y分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标，其中x，y均为正整数.例如，点经过第1次运算得到点，经过第2次运算得到点，以此类推.则点经过2024次运算后得到点__________.
三、解答题
17．（1）计算：；
（2）先化简，再求值：，其中.
18．【实践课题】测量湖边观测点A和湖心岛上鸟类栖息点P之间的距离
【实践工具】皮尺、测角仪等测量工具
【实践活动】某班甲小组根据胡岸地形状况，在岸边选取合适的点B.测量A，B两点间的距离以及和，测量三次取平均值，得到数据：米，，.画出示意图，如图
【问题解决】（1）计算A，P两点间的距离.
（参考数据：，，，，）
【交流研讨】甲小组回班汇报后，乙小组提出了另一种方案：
如图2，选择合适的点D，E，F，使得A，D，E在同一条直线上，且，，当F，D，P在同一条直线上时，只需测量即可.
（2）乙小组的方案用到了________.（填写正确答案的序号）
①解直角三角形②三角形全等
【教师评价】甲、乙两小组的方案都很好，对于实际测量，要根据现场地形状况选择可实施的方案.
19．某学校开展了“校园科技节”活动，活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平，从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩（成绩为百分制，用x表示），并将其分成如下四组：，，，.
下面给出了部分信息：
的成绩为：81，81，82，82，83，83，84，84，84，85，86，86，86，87，88，88，88，89，89，89.
根据以上信息解决下列问题：
（1）请补全频数分布直方图；
（2）所抽取学生的模型设计成绩的中位数是________分；
（3）请估计全校1000名学生的模型设计成绩不低于80分的人数；
（4）根据活动要求，学校将模型设计成绩、科技小论文成绩按的比例确定这次活动各人的综合成绩.
某班甲、乙两位学生的模型设计成绩与科技小论文成绩（单位：分）如下：
通过计算，甲、乙哪位学生的综合成绩更高？
20．列表法、表达式法、图像法是三种表示函数的方法，它们从不同角度反映了自变量与函数值之间的对应关系.下表是函数与部分自变量与函数值的对应关系：
（1）求a、b的值，并补全表格；
（2）结合表格，当的图像在的图像上方时，直接写出x的取值范围.
21．如图，在四边形中，，，.以点A为圆心，以为半径作交于点E，以点B为圆心，以为半径作所交于点F，连接交于另一点G，连接.
（1）求证：为所在圆的切线；
（2）求图中阴影部分面积.（结果保留π）
22．一副三角板分别记作和，其中，，，.作于点M，于点N，如图1.
（1）求证：；
（2）在同一平面内，将图1中的两个三角形按如图2所示的方式放置，点C与点E重合记为C，点A与点D重合，将图2中的绕C按顺时针方向旋转后，延长交直线于点P.
①当时，如图3，求证：四边形为正方形；
②当时，写出线段，，的数量关系，并证明；当时，直接写出线段，，的数量关系.
23．在平面直角坐标系中，点在二次函数的图像上，记该二次函数图像的对称轴为直线.
（1）求m的值；
（2）若点在的图像上，将该二次函数的图像向上平移5个单位长度，得到新的二次函数的图像.当时，求新的二次函数的最大值与最小值的和；
（3）设的图像与x轴交点为，.若，求a的取值范围.
参考答案
1．答案：A
解析：，，，，
而，
平方最大的数是3；
故选A.
2．答案：D
解析：A.该图形是轴对称图形，不是中心对称图形，故此选项不合题意；
B.该图形是轴对称图形，不是中心对称图形，故此选项不合题意；
C.该图形是轴对称图形，不是中心对称图形，故此选项不合题意；
D.该图形既是轴对称图形，又是中心对称图形，故此选项符合题意.
故选：D.
3．答案：C
解析：万，
故选：C.
4．答案：D
解析：A.主视图是等腰三角形，不符合题意；
B.主视图是共底边的两个等腰三角形，故不符合题意；
C.主视图是上面三角形，下面半圆，故不符合题意；
D.主视图是上面等腰三角形，下面矩形，故符合题意；
故选：D.
5．答案：D
解析：A.式子中两项不是同类项，不能合并，故A不符合题意；
B.，故B不符合题意；
C.，故C不符合题意；
D.，故D符合题意.
故选D.
6．答案：B
解析：设改造后每天生产的产品件数为x，则改造前每天生产的产品件数为，
根据题意，得：，
解得：，
经检验是分式方程的解，且符合题意，
答：改造后每天生产的产品件数300.
故选：B.
7．答案：A
解析：正方形，
，
，
，
正n边形的一个外角为，
n的值为；
故选A
8．答案：C
解析：设跳绳、踢毽子、韵律操分别为A、B、C，
画树状图如下，
共有9种等可能的结果，甲、乙恰好选择同一项活动的有3种情况，
故他们选择同一项活动的概率是，
故选：C.
9．答案：B
解析：延长和，交于G点，
四边形是平行四边形，
，即，
，
，，
，
，
又，，
，
，，
，
，
，
，
，
.
故选：B.
10．答案：D
解析：设1班同学的最高身高为，最低身高为，2班同学的最高身高为，最低身高为，
根据1班班长的对话，得，，
，
，
解得，
故①，③正确；
根据2班班长的对话，得，，
，
，
，
故②正确，
故选：D.
11．答案：
解析：原式，
故答案为：.
12．答案：（答案不唯一）
解析：，
由①得：，
由②得：，
不等式组的解集为：，
不等式组的一个整数解为：；
故答案为：（答案不唯一）.
13．答案：
解析：关于x的方程有两个相等的实数根，
，
解得：.
故答案为：.
14．答案：
解析：连接，
，
，
，
，
，
，
，
故答案为：.
15．答案：
解析：如图，过F作于H，
由作图可得：，，，
，
，
，
，
，
F到的距离为；
故答案为：.
16．答案：
解析：点经过1次运算后得到点为，即为，
经过2次运算后得到点为，即为，
经过3次运算后得到点为，即为，
……，
发现规律：点经过3次运算后还是，
，
点经过2024次运算后得到点，
故答案为：.
17．答案：（1）3
（2）
解析：（1）原式.
（2）原式
，
将代入，
原式.
18．答案：（1）A，P两点间的距离为米
（2）②
解析：（1）如图，过B作于H，
米，，，，
，
，
，，
，
，
，
（米）；
即A，P两点间的距离为米；
（2），，当F，D，P在同一条直线上时，
，
，
，
只需测量即可得到长度；
乙小组的方案用到了②.
19．答案：（1）画图见解析
（2）
（3）人
（4）甲的综合成绩比乙高.
解析：（1），而有20人，
有，
补全图形如下：
。
（2），
而的成绩为：81，81，82，82，83，83，84，84，84，85，86，86，86，87，88，88，88，89，89，89.
50个成绩按照从小到大排列后，排在第25个，第26个数据分别是：83，83；
中位数为：；
（3）全校1000名学生的模型设计成绩不低于80分的人数为：
（人）；
（4）甲的成绩为：（分）；
乙的成绩为：（分）；
甲的综合成绩比乙高.
20．答案：（1），补全表格见解析
（2）x的取值范围为或
解析：（1）当时，，即，
当时，，即，
，
解得：，
一次函数为，
当时，，
当时，，即，
反比例函数为：，
当时，，
当时，，
当时，，
补全表格如下：
（2）由表格信息可得：两个函数的交点坐标分别为，，
当的图像在的图像上方时，x的取值范围为或.
21．答案：（1）见解析
（2）
解析：（1）连接如图，
根据题意可知：，，
又，
，
，
，
，
四边形是平行四边形，
，
，
是等边三角形，
，
，
G在以为直径的圆上，
，
为所在圆的切线.
（2）过D作于点H，
由图可得：，
在中，，，
，
，
由题可知：扇形和扇形全等，
，
等边三角形的面积为：，
22．答案：（1）证明见解析
（2）①证明见解析；②当时，线段，，的数量关系为；当时，线段，，的数量关系为
解析：（1）证明：设，
，，
，
，
，
，
，，
，
；
（2）证明：①，，
，，
，
，
，
，
四边形为矩形，
，即，
而，
，
四边形是正方形；
②如图，当时，连接，
由（1）可得：，，
，
，
，
，
，
，
；
②如图，当时，连接，
由（1）可得：，，
，
，
，
，
，
，
.
23．答案：（1）
（2）新的二次函数的最大值与最小值的和为11
（3）
解析：（1）点在二次函数的图像上，
，
解得：，
抛物线为：，
抛物线的对称轴为直线，
；
（2）点在的图像上，
，
解得：，
抛物线为，
将该二次函数的图像向上平移5个单位长度，得到新的二次函数为：
，
，
当时，函数有最小值为1，
当时，函数有最大值为
新的二次函数的最大值与最小值的和为11；
（3）的图像与x轴交点为，.
，，
，
，
，
即，
解得：.
模型设计
科技小论文
甲的成绩
94
90
乙的成绩
90
95
x
a
1
a
1
________
________
________
7
x
1
1
7