山东省枣庄市部分中学2024届九年级下学期中考一模数学试卷(含答案)

这是一份山东省枣庄市部分中学2024届九年级下学期中考一模数学试卷(含答案)，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列运算正确的是( )
A.B.C.D.
2．如图,在中,A、B两个顶点在x轴的上方,点C的坐标是,以点C为位似中心,在x轴的下方作的位似图形,使它与的相似比为,设点B的横坐标是a,则点B的对应点的横坐标是( )
A.B.C.D.
3．如图,在中,以点A为圆心,的长为半径作圆弧交于点D,再分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接交于点E.若的周长为15,,则的长为( )
A.4B.8C.9D.10
4．年技术正式开始商用,它的数据下载的最高速率从初期的提升到,给我们的智慧生活“提速”.其中表示每秒传输10000000000位()的数据.将10000000000用科学记数法表示应为( )
A.B.C.D.
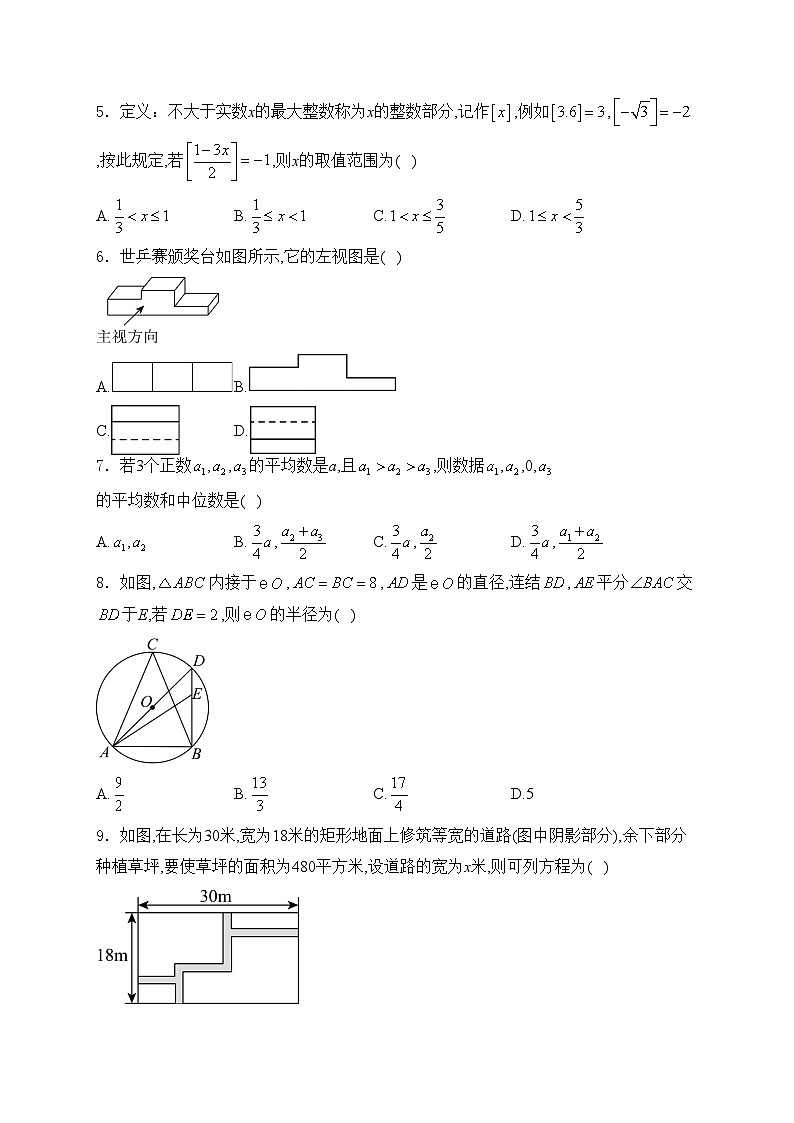
5．定义：不大于实数x的最大整数称为x的整数部分,记作,例如,,按此规定,若,则x的取值范围为( )
A.B.C.D.
6．世乒赛颁奖台如图所示,它的左视图是( )
A.B.
C.D.
7．若3个正数,,的平均数是a,且,则数据,,0,的平均数和中位数是( )
A.,B.,C.,D.,
8．如图,内接于,,是的直径,连结,平分交于E,若,则的半径为( )
A.B.C.D.5
9．如图,在长为30米,宽为18米的矩形地面上修筑等宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为480平方米,设道路的宽为x米,则可列方程为( )
A.B.
C.D.
10．如图,已知二次函数(a,b,c是常数)的图象关于直线对称,则下列五个结论：①；②；③；④(m为任意实数)；⑤.其中正确的是( )
A.①②③B.②③⑤C.①②④⑤D.①②③④⑤
二、填空题
11．在同一平面内,将一副直角三角板ABC和EDF如图放置(,),其中直角顶点D是BC的中点,点A在DE上,则______°.
12．已知实数a,b满足,,则______.
13．已知关于x的方程的解为正数,则m的取值范围为______.
14．如图,在正方形中,O为对角线、的交点,E、F分别为边、上一点,且,连接.若,,则的长为______.
15．如图,在平面直角坐标系中,反比例函数的图象与半径为10的交于A,B两点,若,则k的值是_____.
16．已知一列均不为1的数,,,,满足如下关系：,,,⋯,,若,则的值是______.
三、解答题
17．(1)计算：；
(2)先化简,再求值：,其中.
18．某学校对校内社团活动进行了调查,分别从A足球,B音乐,C舞蹈,D美术,E书法五个项目了解学生的参与情况,对部分学生参与的社团活动类别进行了随机抽样调查,并绘制如下不完整的统计图,请根据图1,图2中所给的信息,解答下列问题：
(1)此次抽样调查的样本容量是_________；
(2)将图1中的条形统计图补充完整；
(3)图2中,“E”所占圆心角的度数是_________；
(4)若该学校共有学生1200人,请估算该校参与足球社团的学生人数.
19．某商场购进了A,B两种商品,若销售10件A商品和20件B商品,则可获利280元；若销售20件A商品和30件B商品,则可获利480元.
(1)求A,B两种商品每件的利润；
(2)已知A商品的进价为24元/件,目前每星期可卖出200件A商品,市场调查反映：如调整A商品价格,每降价1元,每星期可多卖出20件,如何定价才能使A商品的利润最大？最大利润是多少？
20．如图,某校综合实践小组在两栋楼之间的水平地面E处放置一个测角仪,经测量,,,已知米,米.求两栋楼楼顶A,C之间的距离.(参考数据：,,,测角仪的高度忽略不计).
21．如图,一次函数与反比例函数的图象相交于A、B两点,过点B作轴,垂足为C,连接,已知点A的坐标是,.
(1)求反比例函数与一次函数的表达式；
(2)根据图象,直接写出不等式的解集；
(3)点P为反比例函数在第一象限内的图象上一点,若,求点P的坐标.
22．如图,内接于,,是的直径,点P是延长线上的一点,且.
(1)求证：是的切线；
(2)若与交于点M,,且,求阴影部分的面积.
23．综合与实践
问题情境：
如图①,点E为正方形内一点,,将绕点B按顺时针方向旋转,得到(点A的对应点为点C),延长交于点F,连接.
猜想证明：
(1)试判断四边形的形状,并说明理由；
(2)如图②,若,请猜想线段与的数量关系并加以证明；
解决问题：
(3)如图①,若,,请直接写出的长.
24．如图,在平面直角坐标系中,已知抛物线与x轴分别相交于,两点.
(1)求该抛物线的解析式；
(2)点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交于点E,交x轴于点F.
①求的最大值；
②若G是的中点,以点C,D,E为顶点的三角形与相似,求点D的坐标.
参考答案
1．答案：D
解析：A、,原式计算错误,不符合题意；
B、,原式计算错误,不符合题意；
C、,原式计算错误,不符合题意；
D、,原式计算正确,符合题意；
故选：D.
2．答案：A
解析：设点的横坐标为x,
则B、C间的水平距离为,、C间的水平距离为,
∵放大到原来的2倍得到,
,
解得：,
故选：A.
3．答案：B
解析：由题意得,,是的垂直平分线,
∴,
∵的周长为15,
∴,
∴,即,
∴.
故选：B.
4．答案：B
解析：,
故选：B.
5．答案：A
解析：由题意得,,
解得,
故选A.
6．答案：C
解析：∵世乒赛颁奖台如图所示,
∴它的左视图是
故选：C
7．答案：B
解析：∵3个正数,,的平均数是a,
∴,
∴,,0,的平均数为,
∵3个正数,,,且
∴把数据,,0,从大到小排列为,,,0,
∴中位数为,
故选：B.
8．答案：B
解析：过点C作垂直于点,交于点G,交于点H,连接,
∵,
∴为线段的中垂线,,
∵内接于,
∴C,O,K三点共线,,
∴为的直径,
∴,
∵平分,
∴,
∴,
即：,
∴,
∵是的直径,
∴,,
∴,
∴,
∴,
∴,
设半径为r,则：,,
∴,
在中,,
∴,
解得：(舍去)或；
∴的半径为；
故选B.
9．答案：B
解析：利用图形平移可将原图转化为下图,道路的宽为x米.
根据题意可得：.
故选：B.
10．答案：D
解析：抛物线开口往下,
,
抛物线与y轴交于正半轴,
抛物线的对称轴在负半轴,
,
,
,故①正确.
即,故②正确.
抛物线的对称轴为直线,且时,函数值小于零,
与x轴交点到对称轴距离大于1,小于2,
当时,函数值小于零,
即,故③正确.
抛物线的对称轴为直线,且开口向下,
当时,函数值最大,
当时,,
当时,,
,
所以,故④正确.
由函数图象可知,
当时,函数值小于零,
则,
,
所以,故⑤正确.
综上所述：正确的有①②③④⑤.
故选：D.
11．答案：15°
解析：由题得：AD是直角三角形斜边中点,
∴
∵,,
∴是等边三角形,
∴,
∴,
∴.
12．答案：或2
解析：实数a,b满足,,
可将a,b看作是方程的根,
当时,
,
当时,
由根与系数关系可得,,整理代入,
,
故答案为：或2.
13．答案：且
解析：解关于x的分式方程,得：,
根据题意,得∶,且,
解得∶且,
故答案为：且.
14．答案：
解析：在正方形中,和为对角线,
∴,,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
过点F作,如图,
∴,
∵,
∴,
∵,
∴是等腰直角三角形,
又,
∴,
∴
∴
故答案为：.
15．答案：25
解析：设点,
反比例函数的图象与半径为10的交于A,B两点,
所以A,B两点关于直线对称,
,
的半径为10,
,
,即,
,
是等边三角形,
,
,即,
化简得：,
,
,
在反比例函数的图象上,
,
故答案为：25
16．答案：
解析：由题知,因为,
则,
,
,
,
…,
由此可见,这一列数按2,,,循环出现,
且,
所以.
故答案为：.
17．答案：(1)3
(2),
解析：(1)
；
(2)
；
当时,原式.
18．答案：(1)200
(2)图见解析
(3)36
(4)240
解析：(1)(名),
即此次共调查了200名学生.
故答案为：200；
(2)“C舞蹈”的人数为：(名),
补全条形统计图如下：
(3)“E”所在扇形的圆心角为：.
故答案为：36；
(4)(人),
答：估计该校参与足球社团的学生人数约240人.
19．答案：(1)12元,8元
(2)定价为35元时,利润最大,最大为2420元
解析：(1)设A商品每件的利润为x元,B商品每件的利润为y元,
根据题意,得,
解得：,
答：A商品每件的利润为12元,B商品每件的利润为8元.
(2)设降价a元利润为w元根据题意得：
；
,
当时,w有最大值,最大值为2420,
此时定价(元).
答：定价为35元时,利润最大,最大为2420元.
20．答案：A,C之间的距离为100米
解析：如图,过点C作,交于点F.
在中,,
∴是等腰直角三角形,∴米,
在中,,
∴,
∴,∴米.
由题意,得(米),(米),
∴(米),
在中,(米).
∴A,C之间的距离为100米.
21．答案：(1),；
(2)或；
(3).
解析：(1)点在上,
,
∴反比例函数解析式为,
,轴,
∴点B的纵坐标为,
把代入得,,
∴,
,
点、在一次函数图象上,
,
解得,
∴直线的解析式为；
(2)根据图象可得,不等式的解集为或；
(3),
设点P的坐标为,
∵,轴,
∴,
∴,
∵,
,
,
.
22．答案：(1)证明见解析
(2)
解析：(1)证明：连接,,
是圆O的直径,
,
,
,
,
是等边三角形,
,
,
,
,
,
,
点在圆上,
是的切线；
(2)连接,
,
,
,
,
,
,
,
,
,
,
,
,
阴影部分的面积的面积扇形的面积.
23．答案：(1)四边形是正方形,理由见解析
(2),证明见解析
(3).
解析：(1)四边形是正方形
理由：由旋转可知：,,
又,
四边形是矩形.
∵.
四边形是正方形；
(2).
证明：如图,过点D作,垂足为H,
则,
.
四边形是正方形,
,.
,
.
.
∵,
；
(3)如图：过E作
∴
∴
设,则,
在中,,,
∴,即,解得(舍),
∴,
∴,
∴,
∴,
∴
∴.
24．答案：(1)
(2)①9
②或
解析：(1)将,代入抛物线,
得,
解得,
该抛物线的解析式为.
(2)①由抛物线的解析式为,得.
设直线的解析式为,将,代入,
得解得
直线的解析式为.
设第一象限内的点D的坐标为,则,
,,
.
,
当时,有最大值,为9.
②,,,
,,,,
,,,
,
,
.
轴于点F,
,
.
以点C,D,E为顶点的三角形与相似,只需或.
是的中点,,,
,,.
由①知,,
.
当时,,
解得或(舍去),
.
当时,,
解得或(舍去),
.
综上所述,以点C,D,E为顶点的三角形与相似,点D的坐标为或.