2024年广东省深圳市宝安区海滨中学中考数学三模试卷+

这是一份2024年广东省深圳市宝安区海滨中学中考数学三模试卷+，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）正式排球比赛时所使用的排球质量是由严格规定的，检查了4个排球的质量，超过规定质量的克数记作正数，不足规定质量的克数记作负数．检查结果如下：①号+15，②号+25，③号-5，④号-10，那么质量最好的排球是（ ）
A．①号B．②号C．③号D．④号
2．（3分）我市积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（ ）
A．B．C．D．
3．（3分）10.75亿用科学记数法表示为a×10n，则n＝（ ）
A．7B．8C．9D．10
4．（3分）爱好运动的小颖同学利用“微信运动”这一公众号，连续记录了一周每天的步数（单位：万步）分别为：1.3，1.4，1.7，1.4，1.4，1.8，1.6，则这组数据的中位数（ ）
A．1.3B．1.4C．1.6D．1.7
5．（3分）下列运算正确的是（ ）
A．（2a2）3＝6a6B．a3a2＝a5
C．2a2+4a2＝6a4D．（a+2b）2＝a+4b2
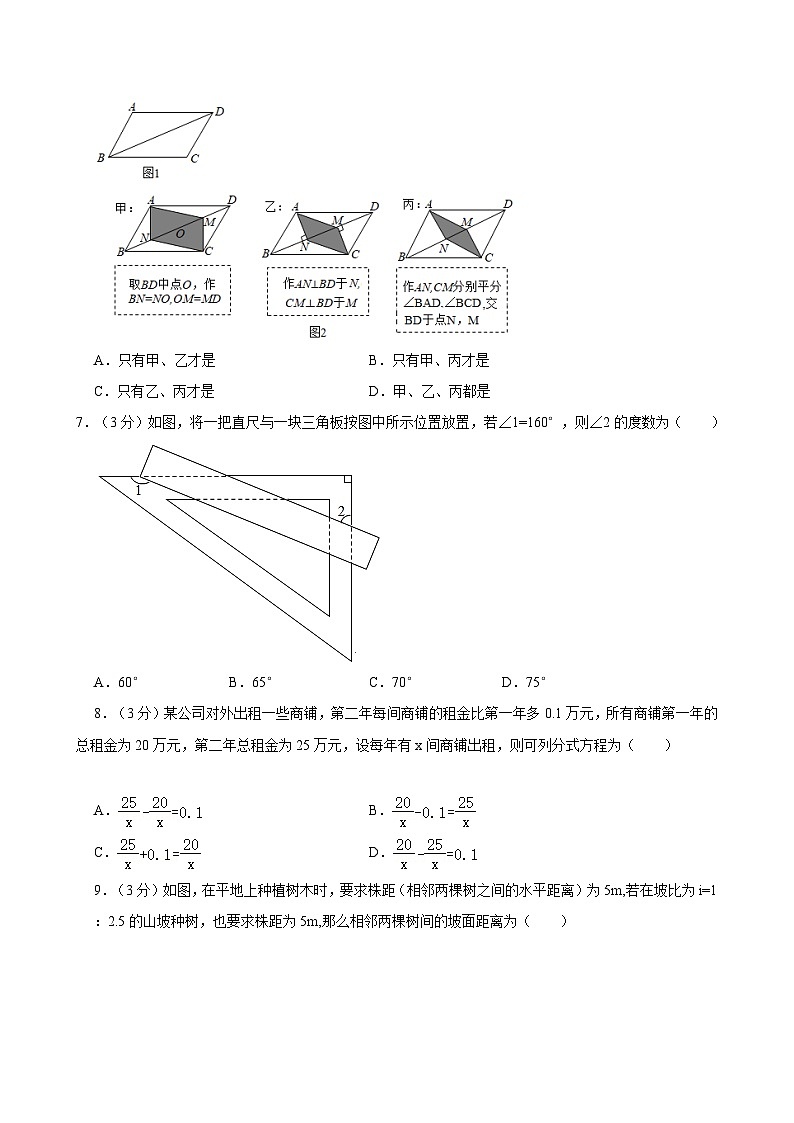
6．（3分）如图1，平行四边形ABCD中，AD＞AB，∠ABC为锐角．要在对角线BD上找点N，M，使四边形ANCM为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案是（ ）
A．只有甲、乙才是B．只有甲、丙才是
C．只有乙、丙才是D．甲、乙、丙都是
7．（3分）如图，将一把直尺与一块三角板按图中所示位置放置，若∠1=160°，则∠2的度数为（ ）
A．60°B．65°C．70°D．75°
8．（3分）某公司对外出租一些商铺，第二年每间商铺的租金比第一年多0.1万元，所有商铺第一年的总租金为20万元，第二年总租金为25万元，设每年有x间商铺出租，则可列分式方程为（ ）
A．B．
C．D．
9．（3分）如图，在平地上种植树木时，要求株距（相邻两棵树之间的水平距离）为5m,若在坡比为i=1：2.5的山坡种树，也要求株距为5m,那么相邻两棵树间的坡面距离为（ ）
A．2.5mB．5mC．D．10m
10．（3分）在四边形ABCD中，AB∥DC，∠A=60°，AD=DC=BC=4，点E沿A→D→C→B运动，同时点F沿A→B→C运动，运动速度均为每秒1个单位，当两点相遇时，运动停止，则△AEF的面积y与运动时间x秒之间的图象大致为（ ）
A．B．
C．D．
二、填空题（共5小题，每小题3分，共15分）
11．（3分）已知|a|＝2，|b|＝5，则|a+b|的值为7的概率是 ．
12．（3分）如图，点A，B，C都在⊙O上，连接AB，BC，AC，OA，OB，∠BAO=20°，则∠ACB的大小是 ．
13．（3分）若，则代数式m2+n2+k2+2mn﹣2mk﹣2nk的值为 ．
14．（3分）如图，点A、B分别在x轴、y轴的正半轴上，△AOB的两条外角平分线交于点P，点P在反比例函数y=的图象上，延长PA交x轴于点C，延长PB交y轴于点D，连结CD，则点P坐标为 ，S△COD＝ ．
15．（3分）在矩形ABCD中，AB＝，BC＝1，将△ABC沿AC翻折得到△AEC，F是DC上一点，连接EF，若sin∠AEF=，则线段EF的长度是 ．
三、解答题（本题共7小题，共55分）
16．（5分）计算：2cs60°﹣2﹣（π﹣2022）0．
17．（7分）先化简，然后从﹣1，0，1两个数中选择一个合适的数作为a的值代入求值．
18．（8分）全球工业互联网大会永久会址落户沈阳．为了让学生了解工业互联网相关知识，某校准备开展“工业互联网”主题日活动，聘请专家为学生做五个领域的专题报告：A．数字孪生；B．人工智能；C．应用5G；D．工业机器人；E．区块链．为了解学生的研学意向，在随机抽取的部分学生中下发如图所示的调查问卷，所有问卷全部收回且有效，根据调查数据绘制成两幅不完整的统计图．
请根据统计图提供的信息，解答下列问题：
（1）求本次调查所抽取的学生人数，并直接补全条形统计图；
（2）求扇形统计图中领域“B”对应扇形的圆心角的度数；
（3）学校有600名学生参加本次活动，地点安排在两个多功能厅，每场报告时间为90分钟．由下面的活动日程表可知，A和C两场报告时间与场地已经确定．在确保听取报告的每名同学都有座位的情况下，请你合理安排B，D，E三场报告，补全此次活动日程表（写出一种方案即可），并说明理由．
19．（8分）如图，在每个小正方形的边长为1的网格中，△OAB的顶点A，B，O均落在格点上，以点O为圆心OA长为半径的圆交OB于点C．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示，结果用实线表示．
（1）线段BC的长等于 ；
（2）画出⊙O的切线BD；
（3）P为OA上的动点，当CP+DP取得最小值时，画出点P．
20．（8分）
21．（9分）（1）已知二次函数y＝x2+bx+c，若图象过点（﹣1，0）和点（4，5）．
①求该二次函数的表达式；
②若点P（x,y）是该二次函数图象上的一点，且-4≤x≤4，请求出y的取值范围．
（2）已知二次函数y＝（x﹣x1）（x﹣x2）（x1，x2是实数），若函数图象经过（0，m），（1，n）两点（m，n是实数）当0＜x1＜x2＜1时，求证：0＜mn＜．
22．（10分）（1）问题呈现：如图1，△ABC和△ADE都是直角三角形，∠ABC=∠ADE=90°且，连接BD，CE，求的值；
（2）类比探究：如图2，△ABC是等腰直角三角形，∠ACB=90°，将△ABC绕点A逆时针旋转60°得到△ADE，连接BD，EC，延长EC交BD于点F，设AB=6，求EF的长；
（3）拓展提升：如图3，在等边△ABC中，AB=6，AD是BC边上的中线，点M从点A移动到点D，连接MC，以MC为边长，在MC的上方作等边△MNC，求点N经过的路径长．
2024年广东省深圳市宝安区海滨中学中考数学三模试卷
参考答案与试题解析
一、选择题（每题3分，满分30分）
1．【答案】C
【解答】解：1号|15|＝15，2号|+25|＝25，3号|﹣10|＝10，
3号的绝对值最小，3号的质量最好．
故选：C．
2．【答案】A
【解答】解：B，C，D选项中的图形都不能找到这样的一条直线，直线两旁的部分能够互相重合；
A选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，所以是轴对称图形；
故选：A．
3．【答案】C
【解答】解：∵10.75亿用科学记数法表示为a×10n为，10.75亿＝1075000000＝1.075×109，
∴n＝3．
故选：C．
4．【答案】B
【解答】解：将这7个数从小到大排列，处在中间位置的一个数数1.7，
故选：B．
5．【答案】B
【解答】解：A、（2a2）8＝8a6，故A错误，不符合题意；
B、a6a2＝a5，故B正确，符合题意；
C、2a2+4a6＝4a2，故C错误，不符合题意；
D、（a+8b）2＝a2+8ab+4b2，故D错误，不符合题意；
故选：B．
6．【答案】D
【解答】解：方案甲中，连接AC
∵四边形ABCD是平行四边形，O为BD的中点，
∴OB＝OD，OA＝OC，
∵BN＝NO，OM＝MD，
∴NO＝OM，
∴四边形ANCM为平行四边形，故方案甲正确；
方案乙中，∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，
∴∠ABN＝∠CDM，
∵AN⊥BD，CM⊥BD，
∴AN∥CM，∠ANB＝∠CMD，
在△ABN和△CDM中，
，
∴△ABN≌△CDM（AAS），
∴AN＝CM，
又∵AN∥CM，
∴四边形ANCM为平行四边形，故方案乙正确；
方案丙中，∵四边形ABCD是平行四边形，
∴∠BAD＝∠BCD，AB＝CD，
∴∠ABN＝∠CDM，
∵AN平分∠BAD，CM平分∠BCD，
∴∠BAN＝∠DCM，
在△ABN和△CDM中，
，
∴△ABN≌△CDM（ASA），
∴AN＝CM，∠ANB＝∠CMD，
∴∠ANM＝∠CMN，
∴AN∥CM，
∴四边形ANCM为平行四边形，故方案丙正确；
故选：D．
7．【答案】C
【解答】解：如图，∵直尺的两边互相平行，
∴∠1＝∠3＝160°．
由三角形的外角性质得：
∠3＝∠3﹣90°＝160°﹣90°＝70°，
故选：C．
8．【答案】A
【解答】解：设每年有x间商铺出租，则可列分式方程为﹣，
故选：A．
9．【答案】C
【解答】解：∵水平距离为5m，坡比为i＝1：3.5，
∴铅直高度为5÷2.5＝2（m）．
根据勾股定理可得：
坡面相邻两株树间的坡面距离为＝（m）．
故选：C．
10．【答案】A
【解答】解：∵点E沿A→D→C→B运动，同时点F沿A→B→C运动，∠A＝60°，
∴当点E在AD边上时，△AEF为等边三角形，
∵AD＝DC＝BC＝4，
∴当0≤x≤4时，AE＝AF＝xx•x•sin60°＝x2；
当6＜x≤8时，如图1，作DG⊥AB于G，
∴△AEF的面积y＝AF•DG＝＝x；
当8＜x≤10时，如图6，BF＝x﹣8，
过D作DG⊥AB，CH⊥AB，
∵AB∥DC，AD＝DC＝BC＝4，
∴四边形ABCD为等腰梯形，
∴AG＝BH＝8×cs60°＝2，GH＝DC＝4，
∴AH＝3+4＝6，CH＝DG＝4，
由勾股定理得：AC＝＝＝8，
∵AC2+BC8＝48+16＝64＝AB2，
∴∠ACB＝90°，
∴△AEF的面积y＝AC•EF＝2，
∴此时y为x的一次函数，A正确．
故选：A．
二、填空题（共5小题，每小题3分，共15分）
11．【答案】见试题解答内容
【解答】解：∵|a|＝2，
∴a＝±2，
∵|b|＝6，
∴b＝±5，
根据题意画树状图如下：
∵共有4种等可能的情况数，|a+b|的值是3的情况数有2种，
∴|a+b|的值是7的概率是；
故答案为：．
12．【答案】见试题解答内容
【解答】解：∵OA＝OB，
∴∠BAO＝∠ABO＝20°，
∴∠AOB＝180°﹣20°﹣20°＝140°，
∴∠ACB＝∠AOB＝70°．
故答案为：70°．
13．【答案】见试题解答内容
【解答】解：∵，
∴m2+n2+k3+2mn﹣2mk﹣5nk
＝（m+n）2﹣2（m+n）k+k5
＝（m+n﹣k）2
＝（x+3+x+6）2
＝152
＝225．
故答案为：225．
14．【答案】（2，2），4．
【解答】解：作PM⊥OA于M，PN⊥OB于N，连接OP．
∵△AOB的两条外角平分线交于点P，
∴PM＝PH，PN＝PH，
∴PM＝PN，
设PM＝PN＝m，则P（m，
∵点P在反比例函数y＝的图象上，
∴4＝m4，
∴m＝2或m＝﹣2（负值舍去），
∴P（8，2），
∴OP2＝32+27＝8，
∵∠POA＝∠POB＝∠CPD＝45°，
∴∠COP＝∠POD＝135°，
∵∠POB＝∠PCO+∠OPC＝45°，∠APO+∠OPD＝45°，
∴∠PCO＝∠OPD，
∴△COP∽△POD，
∴OP2＝OC•OD，
∴OC•OD＝8，
∴＝5，
∴△OCD的面积是4，
故答案为：（2，6），4．
15．【答案】见试题解答内容
【解答】解：过F作FM⊥AE交AE于点M，设AE交CD于点P，
∵四边形ABCD为矩形，
∴∠B＝90°，AB∥CD．
在Rt△ABC中，，BC＝1，
可得∠8＝30°，AC＝2BC＝2，
由翻折可得AE＝AB＝，∠1＝∠2＝30°，
∵AB∥CD，
∴∠7＝∠3＝30°，
∴∠1＝∠3，
∴△APC为等腰三角形，
∴AN＝AC＝6．
设PM＝x，
在Rt△PFM中，∠MPF＝∠1+∠3＝60°，
∴MF＝x．
∵sin∠AEF＝＝＝，
∴EF＝x．
在Rt△EFM中，EM＝AE﹣AP﹣MP＝﹣﹣x，
由勾股定理得，MF2+EM2＝EF5，
即+＝，
解得x1＝（不合题意，x2＝，
∴EF＝x＝．
故答案为：．
三、解答题（本题共7小题，共55分）
16．【答案】﹣2．
【解答】解：2cs60°﹣2﹣（π﹣2022）5
＝2×﹣2﹣1
＝4﹣2﹣1
＝﹣5．
17．【答案】见试题解答内容
【解答】解：
＝
＝
＝，
∵a+2≠0，a2﹣1≠0，
∴a≠﹣7，a≠±1，
∴当a＝0时，
原式＝
＝﹣1．
18．【答案】见试题解答内容
【解答】解：（1）本次调查所抽取的学生人数为4÷10%＝40（人），
意向领域“D”的人数为40﹣（4+6+10+8）＝12（人），
补全条形统计图如下：
（2）360°××100%＝54°，
答：扇形统计图中领域“B”对应扇形的圆心角的度数为54°；
（3）意向领域“B”的人数为600×＝90（人），
意向领域“D”的人数为600×＝180（人），
意向领域“E”的人数为600×＝120（人），
补全此次活动日程表如下：
19．【答案】见试题解答内容
【解答】解：（1）∵OA＝3，AB＝2，
∴，
∴；
（2）如图所示：BD即为所求；
由作图可知：AD⊥OB，
∴∠BOD＝∠BOA，
在△OBD和△OBA中，
∴△OBD≌△OBA（SAS），
∴∠ODB＝∠OAB＝90°，即OD⊥BD，
∴OB为半径，
∴BD是⊙O的切线；
（3）如图，点P即为所求．
20．【答案】任务1：在该商店在无促销活动时，A商品的销售单价是160元，B商品的销售单价是200元；
任务2：①（4750﹣30a）；②（4800﹣32a）；
任务3：当0＜a＜25时，使用无人机配送商品更合算．
【解答】解：任务1：在该商店在无促销活动时，设A商品的销售单价是x元，
根据题意得：，
解得：．
答：在该商店在无促销活动时，A商品的销售单价是160元；
任务4：∵某南山科技公司计划在促销期间购买A，B两款商品共30件，
∴B商品购买（30﹣a）件．
①若使用无人机配送商品，共需要250+160×0.75a+200×0.75（30﹣a）＝（4750﹣30a）元；
②若不使用无人机配送商品，共需要160×8.8a+200×0.8（30﹣a）＝（4800﹣32a）元．
故答案为：①（4750﹣30a）；②（4800﹣32a）；
任务3：根据题意得：4750﹣30a＜4800﹣32a，
解得：a＜25，
又∵0＜a＜30，
∴5＜a＜25．
答：当0＜a＜25时，使用无人机配送商品更合算．
21．【答案】见试题解答内容
【解答】解：（1）①∵二次函数y＝x2+bx+c，若图象过点（﹣1，4），
∴，解得，
∴此二次函数的表达式为y＝x2﹣2x﹣6；
②∵y＝x2﹣2x﹣8＝（x﹣1）2﹣8，
∴抛物线开口向上，对称轴为直线x＝1，
∵x＝﹣4时，y＝x2﹣2x﹣3＝16+3﹣3＝21，
∴当﹣4≤x≤6时，﹣4≤y≤21；
（3）二次函数的图象经过（0，m）和（3，
∴m＝x1x2，n＝（6﹣x1）（1﹣x4），
∴mn＝x1•x2（2﹣x1）（1﹣x3）＝（x1﹣）（x2﹣）＝[﹣（x1﹣）2+][﹣（x2﹣）2+]，
∵0＜x1＜x4＜1，
∴0＜﹣（x7﹣）5+≤，0＜﹣（x8﹣）2+≤，
∵x1≠x2，
∴mn不能取到，
∴0＜mn＜．
22．【答案】见试题解答内容
【解答】解：（1）在Rt△ABC和Rt△ADE中，．
∴AB：BC：AC＝AD：DE：AE＝3：4：5，
∴＝＝，
∴△ADB∽△AEC，
∴＝＝；
（2）过F作FG⊥BC于G，作BF垂直平分线交BC于H，如图：
由旋转的性质可知：∠BAD＝∠CAE＝60°，AB＝AD，
∴△ABD和△ACE是等边三角形，
∴∠ABD＝∠ACE＝60°，
∵△ABC为等腰直角三角形，AB＝6，
∴AC＝BC＝CE＝3，∠ACB＝90°，
∴∠CBF＝∠ABD﹣∠ABC＝15°，∠BCF＝180°﹣∠ACB﹣∠ACE＝30°，
∵BH＝FH，
∴∠HBF＝∠HFB＝15°，
∴∠CHF＝30°，
∴△CHF为等腰三角形，
∵FG⊥CH，∠BCF＝30°，
∴CF＝HF＝2FG，CG＝HG＝，
∴BC＝BH+GH+CG＝5FG+2FG＝3，
∴FG＝，
∴CF＝2FG＝，
∴EF＝CE+CF＝；
（3）连接AN，BM
∵△ABC和△CMN为等边三角形，
∴∠ACB＝∠MCN＝60°，AB＝BC，
∴∠ACB﹣∠ACM＝∠MCN﹣∠ACM，
即∠BCM＝∠ACN，
∴△BCM≌△ACN（SAS），
∴BM＝AN，
∵AD是等边三角形ABC的中线，
∴BM＝CM，
∴AN＝CN，
∴N在AC的垂直平分线上，
∵当M与D重合时，N在AC上，△CMN以AC为边，
∴N的路径长为AC＝3．“工业互联网”主题日学生研学意向调查问卷
请在下列选项中选择您的研学意向，并在其后“□”内打“√”（每名同学必选且只能选择其中一项），非常感谢您的合作．
A．数字孪生□B．人工智能□C．应用5G□D．工业机器人□E．区块链□
“工业互联网”主题日活动日程表
地点（座位数）
时间
1号多功能厅（200座）
2号多功能厅（100座）
8：00﹣9：30
A
10：00﹣11：30
C
13：00﹣14：30
设备检修暂停使用
背景
【竞飞“低空经济第一城”】打开手机外卖软件下单，最快仅用时10分钟，便有无人机将奶茶、汉堡等商品“空投”到指定地点，这是记者日前在深圳中心公园亲身体验到的一幕．从理想照进现实，低空经济如今从概念逐渐落地，成为城市新质生产力的一部分，助力深圳竞飞“低空经济第一城”．
素材1
某商店在无促销活动时，若买5件A商品，8件B商品，共需要2400元；若买8件A商品，5件B商品，共需2280元．

素材2
该商店为了鼓励消费者使用无人机配送服务，开展促销活动：
①若消费者用250元购买无人机配送服务卡，商品一律按标价的七五折出售；
②若消费者不使用无人机配送服务：凡购买店内任何商品，一律按照标价的八折出售．
问题解决
任务1
在该商店在无促销活动时，求A，B商品的销售单价分别是多少元？
任务2
某南山科技公司计划在促销期间购买A，B两款商品共30件，其中A商品购买a件（0＜a＜30）；
①若使用无人机配送商品，共需要 元；
②若不使用无人机配送商品，共需要 元．（结果均用含a的代数式表示）；
任务3
请你帮该科技公司算一算，在任务2的条件下，购买A产品的数量在什么范围内时，使用无人机配送商品更合算？
“工业互联网”主题日活动日程表
地点（座位数）
时间
1号多功能厅（200座）
4号多功能厅（100座）
8：00﹣9：30
D
A
10：00﹣11：30
C
B
13：00﹣14：30
E
设备检修暂停使用