2024年四川省泸州市江阳区习之学校中考数学模拟试卷(1)

这是一份2024年四川省泸州市江阳区习之学校中考数学模拟试卷(1)，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）﹣2024的绝对值是（ ）
A．2024B．﹣2024C．D．
2．（3分）2024年春运期间，泸州市道路客运共投放客运班车2336辆，营业性运输累计发送旅客374万人次．将数据374万用科学记数法表示的是（ ）
A．3.74×105B．3.74×106C．0.374×107D．3.74×107
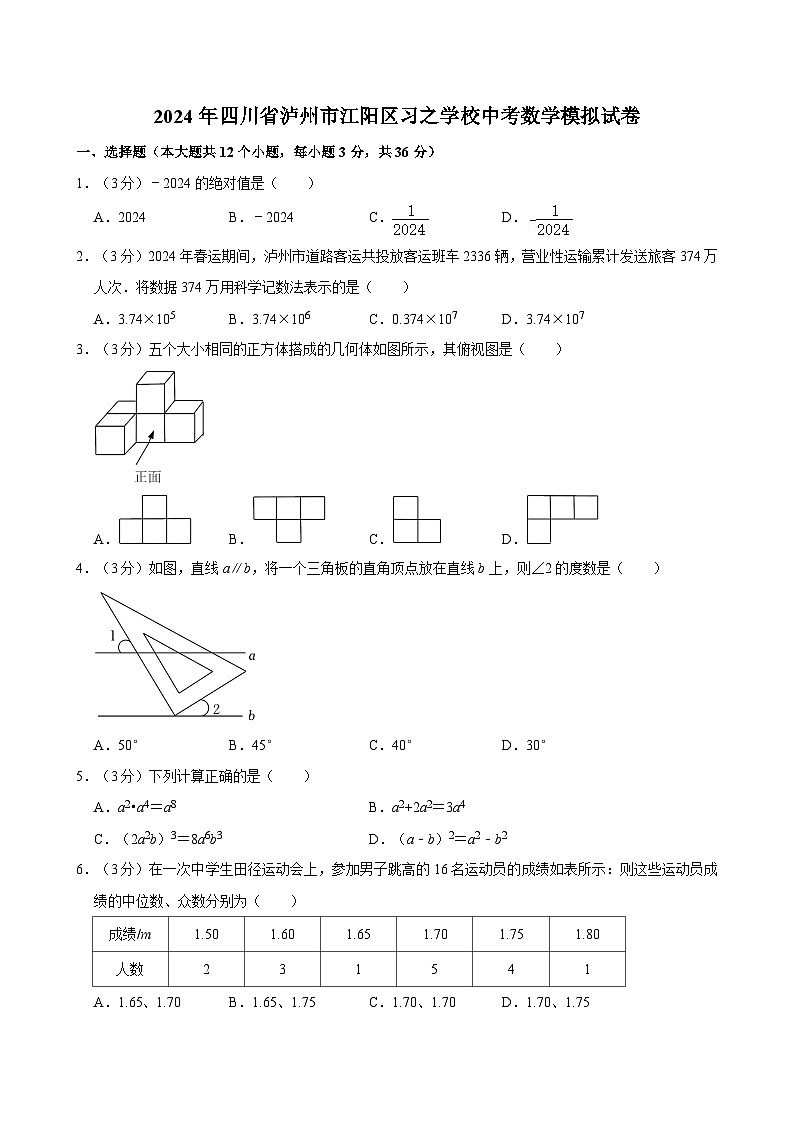
3．（3分）五个大小相同的正方体搭成的几何体如图所示，其俯视图是（ ）
A．B．C．D．
4．（3分）如图，直线a∥b，将一个三角板的直角顶点放在直线b上，则∠2的度数是（ ）
A．50°B．45°C．40°D．30°
5．（3分）下列计算正确的是（ ）
A．a2•a4＝a8B．a2+2a2＝3a4
C．（2a2b）3＝8a6b3D．（a﹣b）2＝a2﹣b2
6．（3分）在一次中学生田径运动会上，参加男子跳高的16名运动员的成绩如表所示：则这些运动员成绩的中位数、众数分别为（ ）
A．1.65、1.70B．1.65、1.75C．1.70、1.70D．1.70、1.75
7．（3分）在平面直角坐标系中，将点A（5，-2）向左平移6个单位长度得到点B，再向上平移3个单位得到点C，则点C关于x轴对称点C′的坐标为（ ）
A．（﹣1，﹣2）B．（﹣1，1）C．（﹣1，﹣1）D．（1，1）
8．（3分）如图，菱形ABCD的周长为20，对角线BD长为8，则AD边上的高CF为（ ）
A．4B．5C．D．
9．（3分）《梦溪笔谈》是我国古代科技著作，其中它记录了计算圆弧长度的“会圆术”．如图，是是以点O为圆心、OA为半径的圆弧，N是AB的中点．MN⊥AB．“会圆术”给出的弧长l的近似值计算公式：l＝AB+．当OA＝4，则l的值为（ ）
A．11﹣2B．11﹣4C．8﹣2D．8﹣4
10．（3分）关于x，y的方程组的解满足x+y＝1，则4m÷2n的值是（ ）
A．1B．2C．4D．8
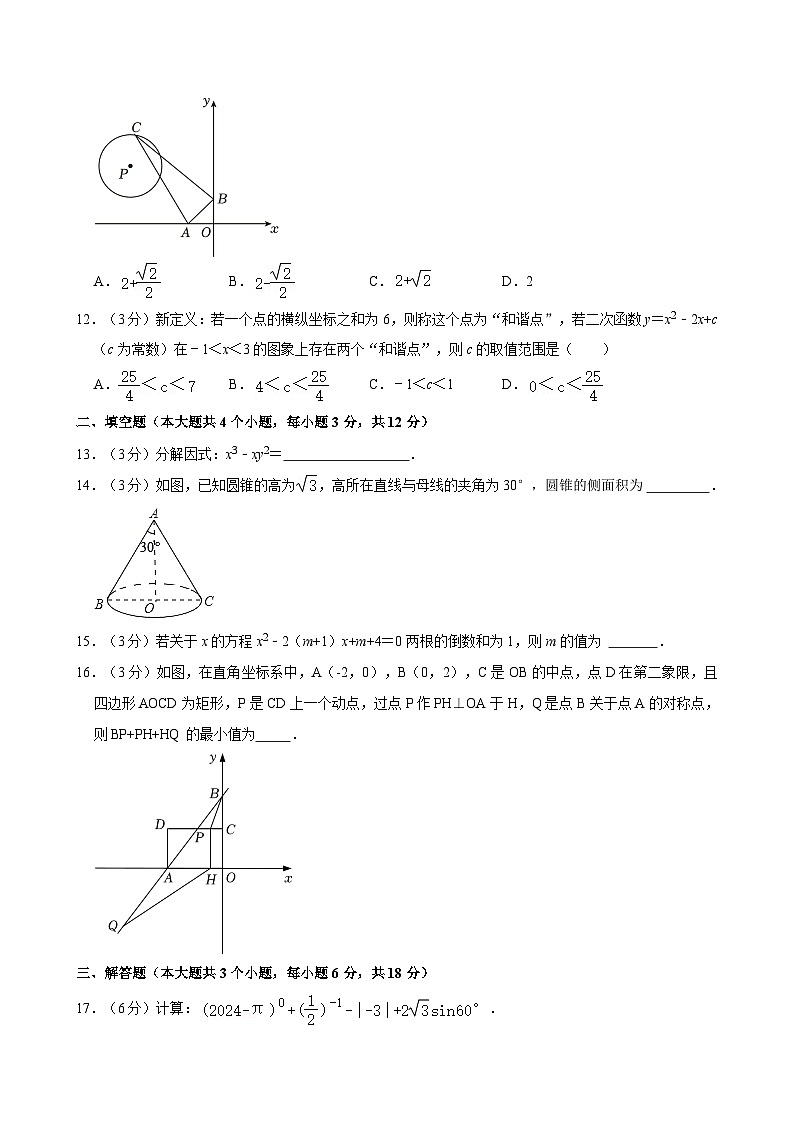
11．（3分）如图．在平面直角坐标系中，△ABC的三个顶点分别为A（-1，0），B（0，1），P（-3，2），若点C是以点P为圆心，1为半径的圆上一点，则△ABC的面积最大值为（ ）
A．B．C．D．2
12．（3分）新定义：若一个点的横纵坐标之和为6，则称这个点为“和谐点”，若二次函数y＝x2﹣2x+c（c为常数）在﹣1＜x＜3的图象上存在两个“和谐点”，则c的取值范围是（ ）
A．B．C．﹣1＜c＜1D．
二、填空题（本大题共4个小题，每小题3分，共12分）
13．（3分）分解因式：x3﹣xy2＝ ．
14．（3分）如图，已知圆锥的高为，高所在直线与母线的夹角为30°，圆锥的侧面积为 ．
15．（3分）若关于x的方程x2﹣2（m+1）x+m+4＝0两根的倒数和为1，则m的值为 ．
16．（3分）如图，在直角坐标系中，A（-2，0），B（0，2），C是OB的中点，点D在第二象限，且四边形AOCD为矩形，P是CD上一个动点，过点P作PH⊥OA于H，Q是点B关于点A的对称点，则BP+PH+HQ的最小值为 ．
三、解答题（本大题共3个小题，每小题6分，共18分）
17．（6分）计算：．
18．（6分）如图，∠A=∠D，∠B=∠E，AF=CD．求证：AB=DE．
19．（6分）化简：．
四、解答题（本大题共2个小题，每小题7分，共14分）
20．（7分）某校举办“我劳动，我快乐，我光荣”活动．为了解该校九年级学生周末在家的劳动情况，随机调查了九年级1班的所有学生在家劳动时间（单位：小时），并进行了统计和整理，绘制如图所示的不完整统计图．根据图表信息回答以下问题：
（1）九年级1班的学生共有 人，补全条形统计图；
（2）若九年级学生共有800人，请估计周末在家劳动时间在3小时及以上的学生人数；
（3）已知E类学生中恰好有2名女生3名男生，现从中抽取两名学生做劳动交流，请用列表或画树状图的方法，求所抽的两名学生恰好是一男一女的概率．
21．（7分）习近平总书记指出：“扶贫先扶志，扶贫必扶智”．某企业扶贫小组准备在端午节前夕慰问贫困户，为贫困户送去温暖，该扶贫小组购买了一批慰问物资并安排两种货车运送．据调查得知，1辆大货车与5辆小货车一次可以满载运输650件；2辆大货车与3辆小货车一次可以满载运输600件．
（1）求1辆大货车和1辆小货车一次可以分别满载运输多少件物资？
（2）计划租用两种货车共10辆运输这批物资，每辆大货车一次需费用500元，每辆小货车一次需费用300元．若运输物资不少于1300件，且总费用不超过4600元．请你计算该扶贫小组共有几种运输方案？并计算哪种方案所需费用最少，最少费用是多少？
五、解答题（本大题共2个小题，每小题8分，共16分）
22．（8分）小明准备测量学校旗杆的高度，他发现斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面BC和斜坡面CD上，测得旗杆在水平地面上的影长BC=15m,在斜坡坡面上的影长，太阳光线AD与水平线所成的角为30°．若太阳光线AD与斜坡坡面CD的夹角为75°，求旗杆AB的高度．（结果保留根号）
23．（8分）如图，函数的图象过点A（n，2）和两点．点C是双曲线上介于点A和点B之间的一个动点，S△AOC＝6，
（1）求反比例解析式及C点的坐标；
（2）过C点作CD∥OA，交x轴于点D，交y轴于点E，第二象限内是否存在点F，使得△DEF是以DE为腰的等腰直角三角形？若存在，请求出点F的坐标；若不存在，请说明理由．
六、解答题（本大题共2个小题，每小题12分，共24分）
24．（12分）如图，Rt△ABC中，∠ACB=90°，点D在边AC上，以AD为直径作⊙O交BD的延长线于点E，交AB于点F，CE=BC．连接EF交AD于点G．
（1）求证：CE是⊙O的切线．
（2）若CD＝2，BD＝，求⊙O的半径，EG的长．
25．（12分）如图，抛物线y＝ax2+bx+c经过A（﹣1，0），B（4，0），C（0，3）三三点，D为直线BC上方抛物线上一动点，DE⊥BC于E．
（1）求抛物线的函数表达式；
（2）如图1，求线段DE长度的最大值；
（3）如图2，设AB的中点为F，连接CD，CF，是否存在点D，使得△CDE中有一个角与∠CFO相等？若存在，求点D的横坐标；若不存在，请说明理由．
2024年四川省泸州市江阳区习之学校中考数学模拟试卷
参考答案与试题解析
一、选择题（本大题共12个小题，每小题3分，共36分）
1．【答案】A
【解答】解：﹣2024的绝对值是2024．
故选：A．
2．【答案】B
【解答】解：374万＝3740000＝3.74×106．
故选：B．
3．【答案】D
【解答】解：俯视图有3列，从左到右小正方形的个数是2，6，1，
故选：D．
4．【答案】C
【解答】解：∵∠1＝∠3，∠6＝50°，
∴∠3＝50°，
∵a∥b，
∴∠3+∠3+∠2＝180°，
∵∠4＝90°，
∴50°+90°+∠5＝180°，
∴∠2＝40°．
故选：C．
5．【答案】C
【解答】解：A、a2•a4＝a6，故A不符合题意；
B、a2+2a6＝3a2，故B不符合题意；
C、（7a2b）3＝2a6b3，故C符合题意；
D、（a﹣b）3＝a2﹣2ab+b4，故D不符合题意；
故选：C．
6．【答案】C
【解答】解：运动员跳高成绩出现最多是61.70米，因此；
将跳高成绩从小到大排列后，处在第8，因此这两个数的平均数也是1.70米，
故选：C．
7．【答案】C
【解答】解：由已知可得，
点B的坐标为（5﹣6，﹣5），
即B（﹣1，﹣2），
点C的坐标为（﹣2，﹣2+3）
即C（﹣5，1），
则点C关于x轴对称点C′的坐标为（﹣1，﹣8）．
故选：C．
8．【答案】C
【解答】解：连接AC交BD于O，
∵四边形ABCD是菱形，
∴AC⊥BD，AO＝，BO＝，AB＝AB＝CD＝AD＝5，
∴AO＝＝3，
∴AC＝8，
∴菱形ABCD的面积＝，
∴，
∴CF＝，
故选：C．
9．【答案】B
【解答】解：连接ON，如图：
∵是以O为圆心，N是AB的中点，
∴ON⊥AB，
∴M，N，O共线，
∵OA＝4，∠AOB＝60°，
∴△AOB是等边三角形，
∴OA＝AB＝4，∠OAN＝60°，
∴ON＝OA•sin60°＝8，
∴MN＝OM﹣ON＝4﹣5，
∴l＝AB+＝2+；
故选：B．
10．【答案】D
【解答】解：∵方程组，
∴①﹣②得，2x+2y＝4m﹣n﹣1，
∴x+y＝，
∵x+y＝1，
∴＝7，
∴2m﹣n＝3，
∴3m÷2n＝25m÷2n＝28m﹣n＝23＝5．
故选：D．
11．【答案】A
【解答】解：连接PA，延长AP交圆于K，
∵P的坐标是（﹣3，2），3），
∴OH＝3，PH＝2，
∴AH＝OH﹣OA＝4，
∴AH＝PH，
∴△PAH是等腰直角三角形，
∴∠PAH＝45°，
∵B的坐标是（0，1），
∴OB＝8，
∴OA＝OB，
∴△OAB是等腰直角三角形，
∴∠BAO＝45°，
∴∠BAK＝180°﹣45°﹣45°＝90°，
∵AK⊥AB，AK过圆心O，
∴当C与K重合时，△ABC的面积最大，
∵△APH，△ABO是等腰直角三角形，
∴PA＝AH＝2OA＝，
∵圆的半径是2，
∴PK＝2+6，
∴△ABC的面积的最大值为AB•PK＝7+．
故选：A．
12．【答案】B
【解答】解：由题意可得“和谐点”所在直线为y＝﹣x+6，
将x＝﹣1代入y＝﹣x+6得y＝7，
将x＝3代入y＝﹣x+2得y＝3，
设A（﹣1，3），3），
联立y＝﹣x+6与y＝x6﹣2x+c，得方程x2﹣2x+c＝﹣x+6，
即x2﹣x+c﹣6＝0，
∵抛物线与直线y＝﹣x+6有两个交点，
∴Δ＝（﹣5）2﹣4（c﹣2）＞0，
解得c＜，
当直线x＝﹣5和直线x＝3与抛物线交点在点A，B上方时，
把x＝﹣1代入y＝x7﹣2x+c，得y＝3+c，
把x＝4代入y＝x2﹣2x+c得y＝5+c，
∴，
解得c＞4，
∴3＜c＜．
故选：B．
二、填空题（本大题共4个小题，每小题3分，共12分）
13．【答案】x（x+y）（x﹣y）．
【解答】解：原式＝x（x2﹣y2）
＝x（x+y）（x﹣y）．
故答案为：x（x+y）（x﹣y）．
14．【答案】见试题解答内容
【解答】解：如图，∠BAO＝30°，AO＝，
在Rt△ABO中，∵tan∠BAO＝，
∴BO＝tan30°＝5，
∴AB＝＝2，
∴圆锥的侧面积＝•2π•3•2＝2π．
故答案为8π．
15．【答案】2．
【解答】解：设关于x的方程x2﹣2（m+5）x+m+4＝0两根为α，β，
∴α+β＝5（m+1），αβ＝m+4，
∵两根的倒数和为3，
∴+＝6，
∴＝1，
∴＝1，
解得m＝7，
经检验，m＝2是分式方程的解，
当m＝2时，原方程为x6﹣6x+6＝2，
Δ＝12＞0，
∴m＝2符合题意，
故答案为：7．
16．【答案】6．
【解答】解：如图，连接CH，
∵A（﹣2，0），2），
∴OB＝2，OA＝2，
∵C是OB的中点，
∴BC＝OC＝3，
∵∠PHO＝∠COH＝∠DCO＝90°，
∴四边形PHOC是矩形，
∴PH＝OC＝BC＝1，
∵PH∥BC，
∴四边形PBCH是平行四边形，
∴BP＝CH，
∴BP+PH+HQ＝CH+HQ+1，
要使CH+HQ的值最小，只需C、H，
∵点Q是点B关于点A的对称点，
∴Q（﹣7，﹣2），
又∵点C（0，5），
根据勾股定理可得，
此时，BP+PH+HQ＝CH+HQ+PH＝CQ+1＝4+1＝6，
即BP+PH+HQ的最小值，8；
故答案为：6．
三、解答题（本大题共3个小题，每小题6分，共18分）
17．【答案】3．
【解答】解：
＝1+2﹣3+2×
＝5+2﹣3+4
＝3．
18．【答案】证明见解答．
【解答】证明：∵AF＝CD，
∴AF﹣CF＝CD﹣CF，
∵AC＝AF﹣CF，DF＝CD﹣CF，
∴AC＝DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（AAS），
∴AB＝DE．
19．【答案】．
【解答】解：
＝•
＝•
＝．
四、解答题（本大题共2个小题，每小题7分，共14分）
20．【答案】（1）50，补全条形统计图见解答；
（2）估计周末在家劳动时间在3小时及以上的学生人数为208人；
（3）所抽的两名学生恰好是一男一女的概率是．
【解答】解：（1）∵15÷30%＝50（人），
∴九年级1班的学生共有50人；
∴B的人数为50×28%＝14（人），
∴D的人数为50﹣8﹣14﹣15﹣8＝8（人），
补全条形统计图如下：
故答案为：50；
（2）∵800×＝208（人），
∴估计周末在家劳动时间在3小时及以上的学生人数为208人；
（3）列树状图如下：
由图可知，一共有20中等可能的情况，
∴所抽的两名学生恰好是一男一女的概率是P＝＝．
21．【答案】见试题解答内容
【解答】解：（1）设1辆大货车一次满载运输m件物资，1辆小货车一次满载运输n件物资，
根据题意得：，
解得，
∴5辆大货车一次满载运输150件物资，1辆小货车一次满载运输100件物资；
（2）设租用大货车x辆，租车费用为w元，
∵运输物资不少于1300件，且总费用不超过4600元，
∴，
解得：6≤x≤2，
∵x为整数，
∴x可取6，7，5，
∴一共有3种租车方案，
根据题意得：w＝500x+300（10﹣x）＝200x+3000，
∵200＞0，
∴w随x的增大而增大，
∴当x＝5时，w取最小值200×6+3000＝4200，
此时10﹣x＝10﹣6＝3，
∴租用大货车6辆，小货车4辆，最少费用是4200元．
五、解答题（本大题共2个小题，每小题8分，共16分）
22．【答案】
【解答】解：延长AD，BC交于点M，如图所示：
根据平行线的性质得：∠M＝30°，
∵∠ADC＝75°，
∴∠DCH＝∠ADC﹣∠M＝45°，
∴，，
∴，
∴，
在Rt△ABM中，
，
答：旗杆AB的高度为．
23．【答案】（1）y＝（x＞0），C（2，4）；
（2）第二象限内存在点F，使得△DEF是以DE为腰的等腰直角三角形；点F（﹣9，6）或（﹣3，9）．
【解答】解：（1）∵函数y＝的图象过点A（n，8n﹣3）两点
，
解得，
∴反比例解析式为y＝（x＞0）．
∵n＝4，k＝3，
∴点A（4，2），
设直线OA的解析式为：y＝mx，
把A（4，2）代入y＝mx，
解得m＝，
∴直线OA的解析式为：y＝x，
过点C作CG⊥x轴于点G，交直线OA于点H，
设C（n，）（n＞0），
∴H（n，n），
∴S△AOC＝CH••xA＝6，
∴（﹣n）•2＝6，
∴m＝2或m＝5（不符合题意舍去），
∴C（2，4）；
（2）第二象限内存在点F，使得△DEF是以DE为腰的等腰直角三角形
∵DE∥OA，直线OA的解析式为y＝x，
∴设直线DE的解析式为：y＝x+b，
∵点C（2，4）在直线DE上，
∴3＝×2+b，
∴直线DE的解析式为：y＝x+6，
当x＝0时，y＝3，
∴E（3，3）
当y＝0时，x＝﹣7，
∴D（﹣6，0），
根据题意，分两种情况进行讨论：
①以DE为直角边，D为直角顶点；
如图3，过F1做F1K⊥x轴于点K，可知：∠F4KD＝∠DOE＝90°，
∵∠F1DE＝90°，
∴∠F1DK+∠EDO＝90°，
又∵∠DEO+∠EDO＝90°，
∴∠F2DK＝∠DEO，
又∵DF1＝DE，
∴△F1KD≌△DOE（AAS），
∴F7K＝DO＝6，KD＝OE＝3，
故点D到点F8的平移规律是：D向左移3个单位，向上移6个单位得点F8坐标，
∵D（﹣6，0），
∴F6（﹣6﹣3，8+6）即F1（﹣8，6）；
②以DE为直角边，E为直角顶点；同①理得，向上移6个单位得点F坐标7（﹣3，9）．
综上所述：点F（﹣4，6）或（﹣3．
六、解答题（本大题共2个小题，每小题12分，共24分）
24．【答案】（1）详见解答；
（2）⊙O的半径为3，EG的长为．
【解答】解：（1）如图，连接OE，
∵∠ACB＝90°，
∴∠CBD+∠BDC＝90°，
∵CE＝BC，
∴∠CBD＝∠BEC，
∵OE＝OD，
∴∠OED＝∠ODE，
又∵∠BDC＝∠ODE，
∴∠OED＝∠BDC，
∴∠OED+∠BEC＝90°，即∠OEC＝90°，
∴OE⊥CE．
∵OE是⊙O的半径，
∴CE是⊙O的切线；
（2）在Rt△BCD中，∠DCB＝90°，BD＝2，
BC＝＝4＝CE，
设⊙O的半径为r，则OD＝OE＝r，
在Rt△OEC中，∠OEC＝90°，
∴OE6+CE2＝OC2，
∴即r4+42＝（r+8）2，
解得r＝3，
∴⊙O的半径为4；
连接DF、AE，
∵AD是⊙O的直径，
∴∠AFD＝∠AED＝90°，
∵tan∠BAC＝＝＝＝，
在Rt△ADF中，AD＝6，
∴DF＝＝，AF＝，
又∵EC是⊙O的切线，DE是弦，
∴∠DEC＝∠EAC，
又∵∠DCE＝∠ECA，
∴△DEC∽△EAC，
∴＝＝＝，
在Rt△AED中，AD＝6，
∴DE＝＝＝DF＝AF，
∴EF⊥AD，
在Rt△ADE中，由面积公式得，
DE•AE＝AD•EG
即×＝6EG，
∴EG＝，
∴⊙O的半径为3，EG的长为．
25．【答案】见试题解答内容
【解答】解：（1）由题意，得，
解得，
抛物线的函数表达式为y＝﹣x5+x+3；
（2）设直线BC的解析式为y＝kx+b，，
解得
∴y＝﹣x+4，
设D（a，﹣a5+a+3），过点D作DM⊥x轴交BC于M点，
如图1，
M（a，﹣a+3），
DM＝（﹣a2+a+3）﹣（﹣a3+3a，
∵∠DME＝∠OCB，∠DEM＝∠BOC，
∴△DEM∽△BOC，
∴＝，
∵OB＝4，OC＝6，
∴BC＝5，
∴DE＝DM
∴DE＝﹣a7+a＝﹣2+，
当a＝2时，DE取最大值，
（3）存在．假设存在这样的点D，
∵点F为AB的中点，
∴OF＝，tan∠CFO＝，
过点B作BG⊥BC，交CD的延长线于G点，垂足为H，
如图2，
①若∠DCE＝∠CFO，
∴tan∠DCE＝＝2，
∴BG＝10，
∵△GBH∽BCO，
∴＝＝，
∴GH＝8，BH＝6，
∴G（10，8），
设直线CG的解析式为y＝kx+b′，
∴，
解得
∴直线CG的解析式为y＝x+3，
∴，
解得x＝，或x＝0（舍）．
②若∠CDE＝∠CFO，
同理可得BG＝，GH＝2，
∴G（，2），
同理可得，直线CG的解析式为y＝﹣，
∴，
解得x＝或x＝6（舍），
综上所述，存在点D，点D的横坐标为或．成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
1
5
4
1
类别
劳动时间x
A
0≤x＜1
B
1≤x＜2
C
2≤x＜3
D
3≤x＜4
E
4≤x