中职数学北师大版（2021）拓展模块一 上册6.4.1 平面与平面平行备课ppt课件

这是一份中职数学北师大版（2021）拓展模块一 上册6.4.1 平面与平面平行备课ppt课件，共15页。PPT课件主要包含了空间中平行关系的定义，两个平面的位置关系，两个平面平行，两个平面相交，两个平面没有公共点，平面与平面平行，线面平行面面平行，交线与交线平行，⇒a∥b，面面平行线线平行等内容，欢迎下载使用。
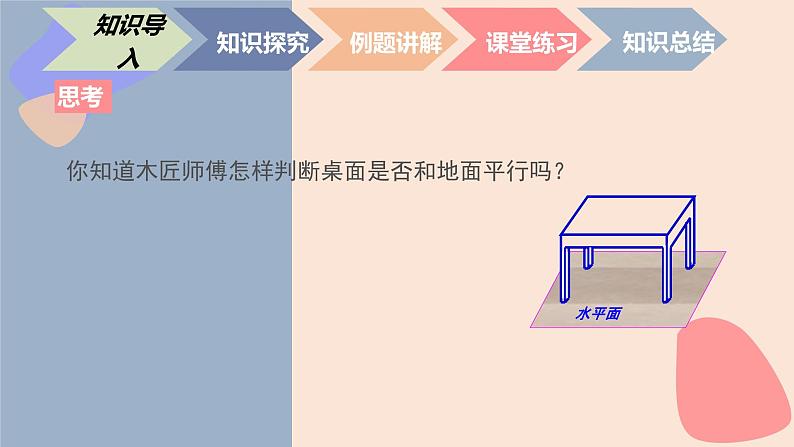
你知道木匠师傅怎样判断桌面是否和地面平行吗？
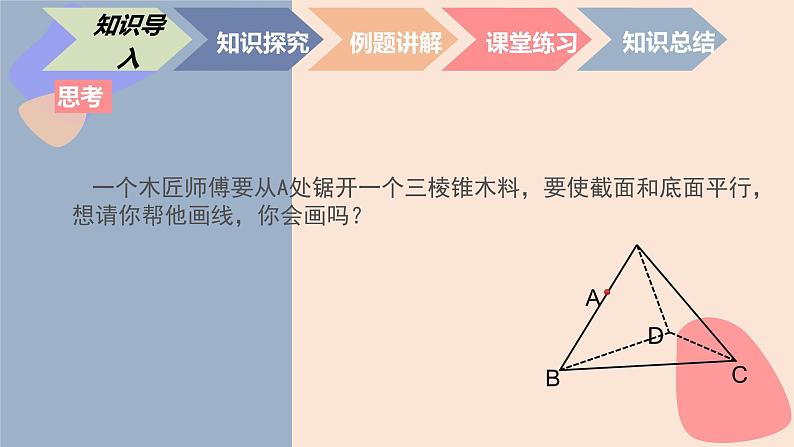
一个木匠师傅要从A处锯开一个三棱锥木料，要使截面和底面平行，想请你帮他画线，你会画吗？
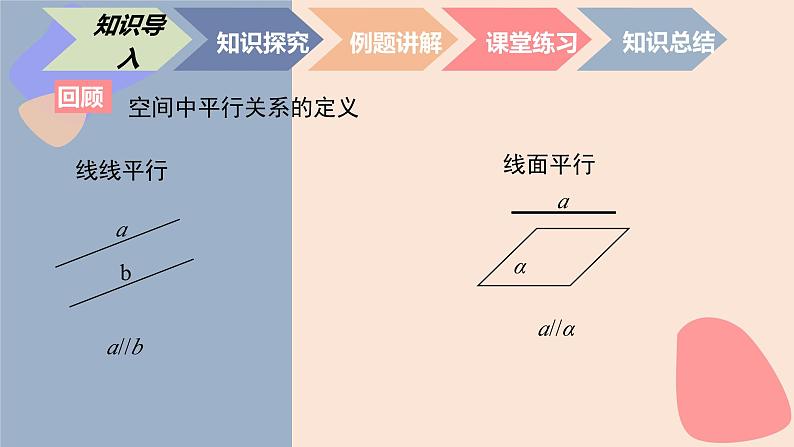
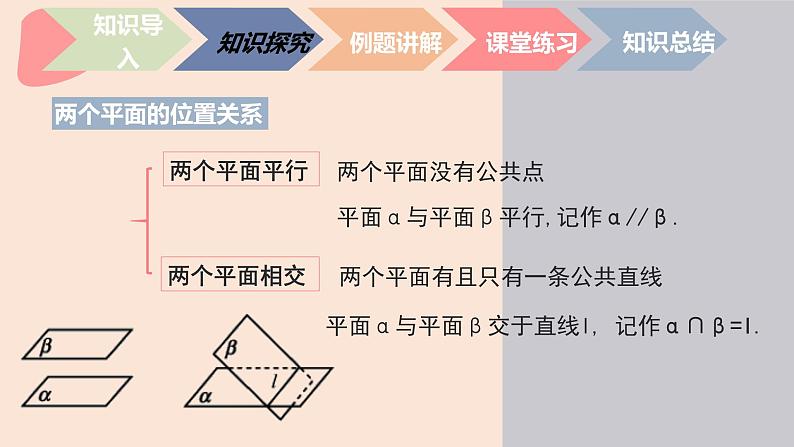
平面α与平面β平行,记作α//β.
两个平面有且只有一条公共直线
平面α与平面β交于直线l, 记作α∩β=l.
①三角板的一条边所在直线与桌面平行，这个三角板所在平面与桌面平行吗？
②三角板的两条边所在直线分别与桌面平行，三角板所在平面与桌面平行吗？
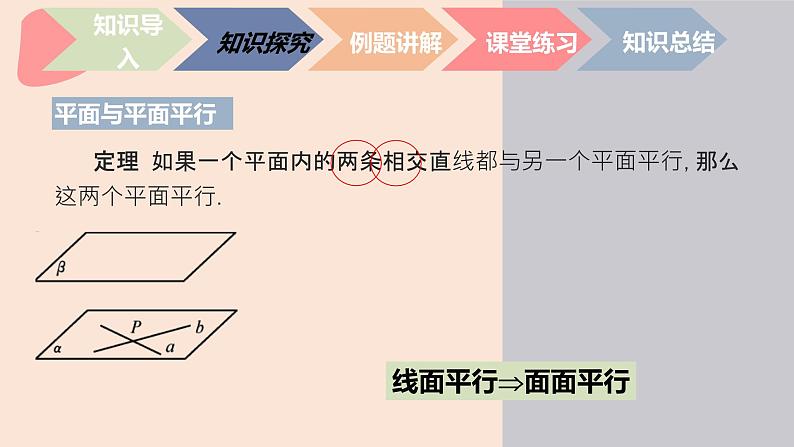
定理 如果一个平面内的两条相交直线都与另一个平面平行,那么这两个平面平行.
1.辨析(正确的画“√”，错误的画“×”)(1)α内有无数多条直线与β平行，则α∥β. (　　)(2)α内的任何直线都与β平行，则α∥β. (　　)(3)直线a∥α，a∥β，则α∥β. (　　)(4)直线a⊂α，直线b⊂β，且a∥β，b∥α，则α∥β. (　　)
定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
α∥βα∩γ= a β∩γ= b
例1 如图,在三棱锥P-ABC中,D,E,F分别为棱PA,PB,PC的中点,求证:平面ABC∥平面DEF.
证明:连接 DE,DF,EF.
因为D,E,F分别是PA,PB,PC的中点,
所以DE∥AB,DF∥AC.
又因为DE⊂平面DEF,DF⊂平面DEF,DE∩DF=D,
AB⊂平面ABC,AC⊂平面ABC,AB∩AC=A,
所以由平面与平面平行的判定定理的推论得平面ABC∥平面DEF.
证明： AB ∩ CD = O ,将AB与CD确定的平面记为平面 γ ,
∴点 A , B , C , D , O 都在平面 γ 内,
∴ α ∩ γ = AC , β ∩ γ = BD .
又∵ α ∥β , ∴由平面与平面平行的性质定理得AC∥BD ,
例 2 如图 ，平面α与平面β平行, 直线AB 分别交平面α , β于点A , B , 直线CD分别交平面α , β于点C , D , AB ∩ CD = O , 点O在两个平面之间, AO =5 , BO =10 , CO =6 , 求CD.
∴ △ OAC ∽△ OBD ,
∴ ∠ A =∠ B , ∠ C =∠ D ,
AO/BO =CO/DO
又∵ AO =5 , BO =10 , CO =6 ,
∴ DO =12 ,∴ CD = CO + DO =18.
1. 已知α∥β, a⊂α, b⊂β,则a与b的关系为( ) . A. 相交 B.平行 C.异面 D. 平行或异面 2. 下列说法错误的是( ) . A. 如果一个平面内的任一直线都平行于另外一个平面, 那么这两个平面平行. B. 如果两个平面平行, 那么其中一个平面内的直线必平行于另外一个平面. C. 分别在两个平行平面内的两条直线一定平行. D. 若一个平面与两个平行平面相交, 则交线必平行.3. 空间两个平面的位置关系有______和______.