中职数学北师大版（2021）拓展模块一 下册7.1.2 复数的几何意义课堂教学ppt课件

这是一份中职数学北师大版（2021）拓展模块一 下册7.1.2 复数的几何意义课堂教学ppt课件，共16页。PPT课件主要包含了知识回顾，复数的几何意义，有序数对ab，坐标系中的点，复平面，b＝0，a＝0，复数的向量表示，几何意义，复数的模等内容，欢迎下载使用。

形如 a + bi (a, b∈R)的数叫作复数，
我们知道，实数与数轴上的点一一对应，可以用数轴上的点表示实数.
提问：复数z=a+bi(a，b∈R)，是否可以与点(a,b)一一对应?
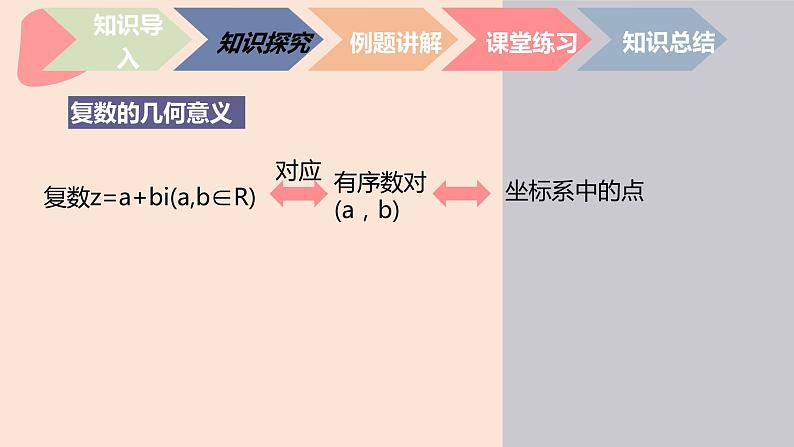
复数z=a+bi(a,b∈R)
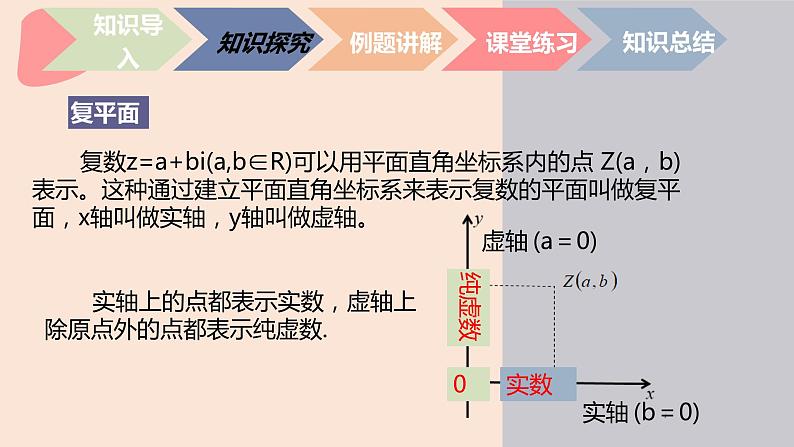
复数z=a+bi(a,b∈R)可以用平面直角坐标系内的点 Z(a，b)表示。这种通过建立平面直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴叫做虚轴。
实轴上的点都表示实数，虚轴上除原点外的点都表示纯虚数.
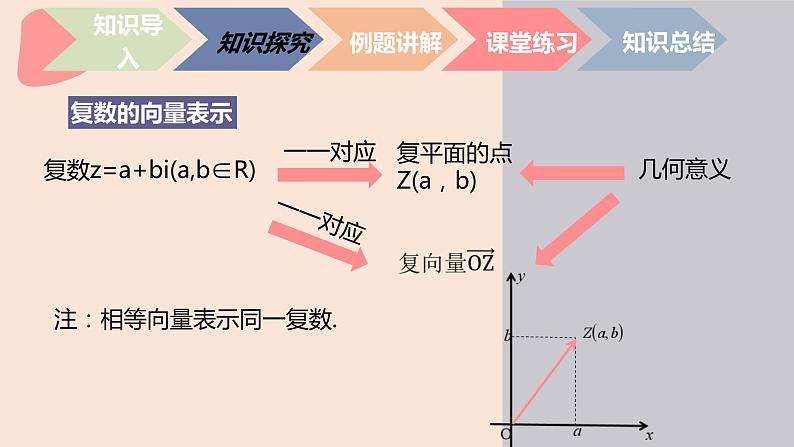
复平面的点Z(a，b)
注：相等向量表示同一复数.
①如果b=0，那么z=a+bi是一个实数a，
②如果a=0，那么z=a+bi是一个纯虚数，
例1 在复平面内分别画出表示下列复数的点，并分别求出它们的模.
例2 将复数z1=－2i,z2=3,z3=1－i,z4=1+i用向量表示.
练习：1、在复平面内画出下列复数所对应的点，并分别求出它们的模.
练习：2、写出图中各点所表示的复数.
点E表示复数z5=1-2i.
点A表示复数z1=2；
点B表示复数z2=i；
点C表示复数z3=-2+3i；
点D表示复数z4=-3-2i；
练习：3. 在复平面内，作出下列复数对应的向量.