2023-2024学年第二学期浙江省温州市数学八年级期末模拟练习卷（解析版）

这是一份2023-2024学年第二学期浙江省温州市数学八年级期末模拟练习卷（解析版），文件包含2023-2024学年第二学期浙江省温州市数学八年级期末模拟练习卷解析版docx、2023-2024学年第二学期浙江省温州市数学八年级期末模拟练习卷docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

在每小题给出的四个选项中，只有一项是符合题目要求的。
1．下列图形中，成中心对称图形的是（ ）
A．B．C．D．
【答案】B
【分析】本题考查了中心对称图形的定义，根据中心对称图形的定义：把一个图形绕某一点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，掌握中心对称图形的定义是解题的关键．
【详解】、不是中心对称图形，故本选项不符合题意；
、是中心对称图形，故本选项符合题意；
、不是中心对称图形，故本选项不符合题意；
、不是中心对称图形，故本选项不符合题意；
故选：．
2.下列实数的取值能使代数式有意义的是（ ）
A．B．C．D．
【答案】C
【分析】根据二次根式有意义条件以及分母不为0即可作答．
【详解】解：因为，
所以分母不为0，即，则，
因为二次根式有意义，即，
那么的取值为且，
故选：C．
3．已知关于的一元二次方程有两个相等的实数根，则值是（ ）
A．0B．1C．2D．4
【答案】D
【分析】由方程有两个相等的实数根，可得出关于m的一元一次方程，解之即可得出结论．
【详解】方程有两个相等的实数根，
= ，
解得：m = 4，
故选：D．
4．如图，在▱ABCD中，下列说法一定正确的是（ ）

A．AC＝BDB．AC⊥BDC．AB＝CDD．AB＝BC
【答案】C
【详解】解：∵平行四边形的两组对边分别平行且相等，对角线互相平分，
∴C正确，其余不一定正确，
故选C．
5．已知一组数据：35，33，31，35，36，这组数据的平均数和中位数分别是（ ）
A．34，35B．34，34C．35，34D．35，35
【答案】A
【分析】根据平均数和中位数的定义进行求解即可．
【详解】解：这组数据的平均数为，
将这组数据从小到大排列为31，33，35，35，36，处在最中间的数据是35，
∴中位数是35，
故选A．
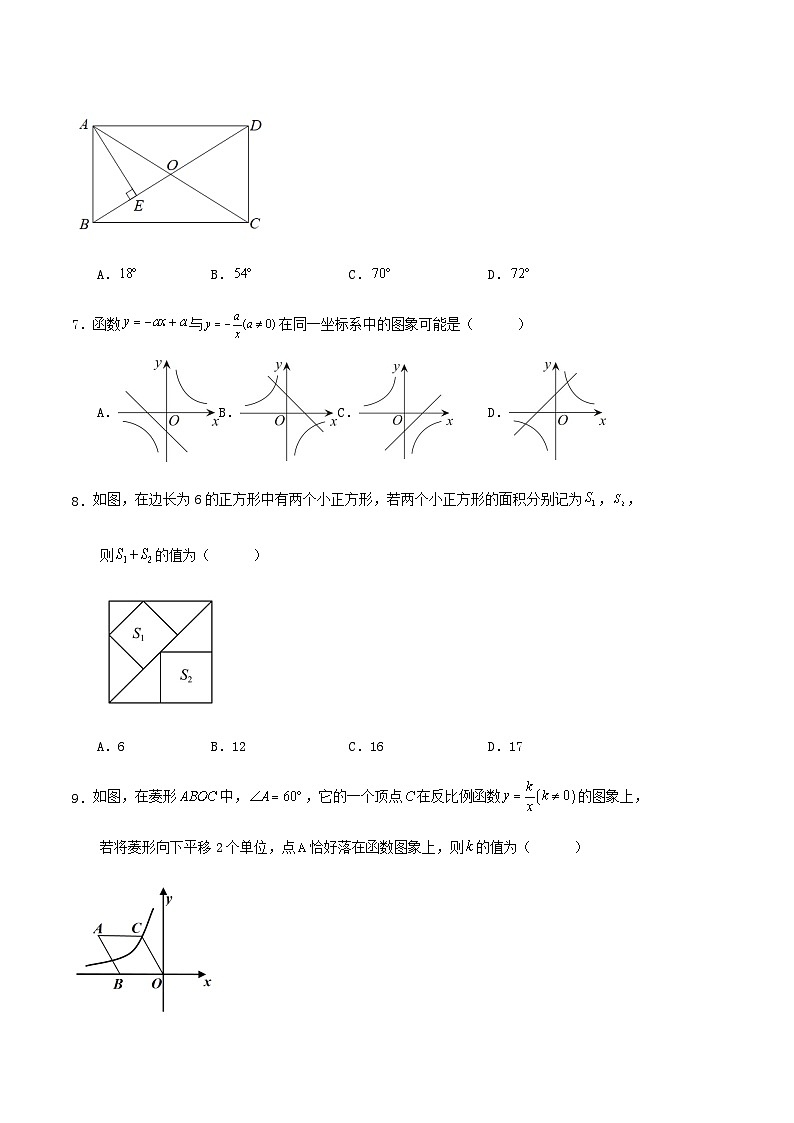
如图，矩形中，对角线与相交于点，于点，
若，则的度数为（ ）
A．B．C．D．
【答案】D
【分析】根据矩形的性质得到∠OAB=∠OBA，再根据∠BAE=2∠OAE，结合垂线的定义得到2∠OAE+3∠OAE=90°，解之可得∠OAE，从而求出∠AOB．
【详解】解：∵四边形ABCD是矩形，
∴OA=OB，
∴∠OAB=∠OBA，
∵∠BAE=2∠OAE，
∴∠OBA=∠OAB=3∠OAE，
∵AE⊥OB，
∴∠BAE+∠OBA=90°，
∴2∠OAE+3∠OAE=90°，
解得：∠OAE=18°，
∴∠AOB=90°-18°=72°，
故选D．
7．函数与在同一坐标系中的图象可能是（ ）
A．B．C．D．
【答案】B
【分析】根据反比例函数与一次函数的图象特点，依次判断，即可求解，
本题主要考查了反比例函数的图象性质和一次函数的图象性质，关键是由a的取值确定函数所在的象限．
【详解】解：当时，，在一、二、四象限，在二、四象限，只有B符合，
当时，，在二、三、四象限，在一、三象限，无选项符合，
故选：B．
如图，在边长为6的正方形中有两个小正方形，若两个小正方形的面积分别记为，，
则的值为（ ）

A．6B．12C．16D．17
【答案】D
【分析】本题考查了勾股定理，等腰直角三角形的性质．由图可得，的边长为3，由，，可得，，；然后，分别算出、的面积，即可解答．
【详解】解：如图：
设正方形的边长为，
和都为等腰直角三角形，
，，，
∴，同理可得：，
，又，
，
，即；
的面积为；
，
，
，
，
为的中点，
的边长为3，
的面积为，
．
故选：D．
如图，在菱形中，，它的一个顶点在反比例函数的图象上，
若将菱形向下平移2个单位，点恰好落在函数图象上，则的值为（ ）
A．B．C．D．
【答案】B
【分析】过点C作CD⊥x轴于D，设菱形的长为a，根据菱形的性质和三角函数分别求出C，以及点A向下平移2个单位长度的点，再根据反比例函数图象上点的坐标特征得到方程组求解即可．
【详解】解：过点C作CD⊥x轴于D，
设菱形的长为a，
在Rt△CDO中，OD==，CD==，
则点C(-,)，
点A向下平移2个点的坐标为(,)，即点A(,)，
则
解得
故选B．
如图，正方形ABCD中，AC，BD相交于点O，E为线段BO上一动点（不包括O，B两点），
DF⊥CE于点F，过点A作AG⊥DF于点G，交BD于点H，连结AE，CH，则下列结论：
①∠ADG＝∠DCF；②DG＝EF；③存在点E，使得EF＝GF；④四边形AECH是菱形．
其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
解：∵四边形ABCD是正方形，DF⊥CE
∴∠ADC＝90°，∠DFC＝90°，
∴∠ADG＝90°﹣∠FDC＝∠DCF，故①正确；
在△ADG和△DCF中，
∠AGD=∠DFC∠ADG=∠DCFAD=CD，
∴△ADG≌△DCF（AAS），
∴DG＝CF，
∵E为动点，
∴DE不一定等于DC，
∴CF不一定等于EF，
∴DG不一定等于EF，故②错误；
∵DF⊥CE，AG⊥DF，
∴CE//AG，
∴∠ECA＝∠HAC，
∵四边形ABCD是正方形，
∴直线BD为正方形ABCD的对称轴，AC⊥BD，OA＝OC，
∴AH＝CH，
∴∠HAC＝∠HCA，
∴∠ECA＝∠HCA，
∴OE＝OH，
∴四边形AECH对角线互相垂直平分，
∴四边形AECH是菱形，故④正确；
∴CE＝AH，
∴HG＝AG﹣AH＝AG﹣CE，
而△ADG≌△DCF有AG＝DF，DG＝CF，
∴HG＝DF﹣CE＝（DG+GF）﹣（CF+EF）＝GF﹣EF，
∵E为线段BO上一动点（不包括O，B两点），
∴HG≠0，即GF﹣EF≠0，
∴GF≠EF，故③不正确；
∴正确的有①④，
故选：B．
二．填空题（本大题共6小题，每小题4分，共24分，把答案直接填在答题卡相应位置上）
11．二次根式中，字母x的取值范围是 ．
【答案】
【分析】本题考查二次根式有意义的条件，根据二次根式的被开方数为非负数，进行求解即可．
【详解】解：由题意，得：，
∴；
故答案为：．
12．方程有两个相等的实数根，则m的值为 ．
【答案】1
【分析】根据一元二次方程根的判别式，列出方程，即可求解．
【详解】解：方程有两个相等的实数根，
，
解得，
故答案为：1．
13.小丽参加单位举行的演讲比赛，评分规则及小丽的得分如下表：
则小丽的最终演讲评分为 ．
【答案】85.5
【分析】使用加权平均数进行计算即可．
【详解】
故答案为：85.5．
14 .如图，在反比例函数和的图象上取两点，若轴，的面积为，则K ．
【答案】
【分析】根据S△OBC-S△OAC=5求解即可．
【详解】解：∵轴，
∴S△OBC=k，S△OAC=×4=2，
∵的面积为，
∴S△OBC-S△OAC=5，
∴k-2=5，
∴k=14，
故答案为：14．
15．中国“一带一路”倡议给沿线国家带来很大的经济效益．若沿线某地区居民2017年人均收入300美元，预计2019年人均收入将达到432美元，则2017年到2019年该地区居民年人均收入增长率为 .
【答案】20
【分析】设该地区人均收入增长率为x，根据2017年人均收入300美元，预计2019年人均收入将达到432美元，可列方程求解.
【详解】解：设该地区人均收入增长率为x，
则300×（1+x）2=432，
∴（1+x）2=1.44，
解得x=0.2（x=-2.2舍），
∴该地区人均收入增长率为20％.
故本题答案应为：20％.
如图，将矩形纸片对折，使边与完全重合，得到折痕，再一次折叠纸片，
使点落在上，得到折痕．

（1）则 ；
（2）若射线恰好经过点，则的值为 ．
【答案】 ,
【分析】（1）如图所示，延长交于点，根据折叠可得，可知，根据矩形的性质，矩形的折叠，可得点分别为的中点，是直角三角形，可得，且，可得，在中，根据直角边与斜边的关系即可求解；
（2）根据题意可得，在中，是中位线，可知点是线段的中点，根据折叠三角形全等的性质可得，在中，根据含特殊角的直角三角形边的关系，矩形的性质的综合即可求解．
【详解】解：（1）如图所示，延长交于点，

∵四边形是矩形，是折痕，
∴四边形，四边形都是矩形，，
∴，点分别为的中点，
∴，
∵沿折叠得，
∴，
∴，
∵点分别为的中点，
∴，
∵，
∴，则，
∵，
∴是直角三角形，
∴在中，，
∴，
∴，
∴，
故答案为：；
（2）根据题意，作图如下，即射线恰好经过点，

由（1）可知，，
∴， ，
∵四边形是矩形，是对角线，是折痕，且点分别为的中点，，
∴在中，是中位线，
∴点是线段的中点，即，
∴，
∴在中，，
∴，
∵四边形是矩形，
∴，
∴，即，
故答案为：．
解答题：本题共8小题，共66分。解答应写出文字说明、证明过程或演算步棸。
17．计算
(1)
(2)
【答案】(1)
(2)
【分析】（1）先计算二次根式乘除法，再计算加减即可；
（2）先用平方差与完全平方公式计算，再合并即可．
【详解】（1）解：原式
；
（2）解：原式
．
18．解方程：
(1)；
(2)．
【答案】(1)，
(2)，
【分析】（1）先移项，再利用提公因式分解法解一元二次方程即可；
（2）根据配方法求解一元二次方程即可．
【详解】（1）解：，
，
，
或，
，．
（2）解：，
，
，
，
，
，．
19．为迎接杭州亚运会，学校举办“亚运会知识竞赛”，初赛共道题，每题分，小乘从初赛名单中随机抽取部分同学的成绩，绘制出如下的统计图和图．请根据相关信息，解答下列问题：

(1)图中的值为______，补全条形统计图；
(2)求被抽取的初赛成绩的平均数，众数和中位数；
(3)如果初赛成绩在分或分以上的同学进入复赛，
请估计参加初赛的位同学中有多少同学可以参加复赛．
【答案】(1)，图见解析
(2)分；分；分
(3)人
【分析】（1）求出调查总人数，即可确定出的值；
（2）求出这组数据的平均数，众数，以及中位数即可；
（3）求出初赛成绩在分或分以上的同学占的百分比，乘以即可得到结果．
【详解】（1）解：根据题意得：（人），，即，
故答案为：，
成绩为70分的有人，
补全条形统计图如下：

（2）（分），
这组数据的平均数是分；
这组数据中，分出现了次，出现次数最多，
这组数据的众数为分；
将这组数据按照从小到大顺序排列，其中处于中间的两个数都是分，，
这组数据的中位数为分；
（3）根据题意得：（人），
则参加复赛的同学大约有人．
20．图1，图2中的小正方形的边长均为1，线段AB，EF的端点A，B，E，F均在小正方形的顶点上．
（1）在图1中画出一个以线段AB为边的平行四边形ABCD，点C，D均在小正方形的顶点上，
且平行四边形ABCD的面积为8；
在图2中画出以线段EF为边的菱形EFGH，点G，H均在小正方形的顶点上，
且菱形EFGH的面积为8，连接FH，直接写出FH的长．

解：（1）如图，四边形ABCD即为所求；
（2）如图，四边形EFGH即为所求．FH=42+42=42．

某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，
且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，
该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）该经销商想要每天获得150元的销售利润，销售价应定为多少？
解：（1）由图象知，（10，40），（18，24），
设y与x之间的函数关系式y＝kx+b（k≠0），
把（10，40），（18，24）代入得：
10k+b=4018k+b=24，
解得：k=−2b=60，
∴y与x之间的函数关系式y＝﹣2x+60（10≤x≤18）；
（2）根据题意得：（x﹣10）（﹣2x+60）＝150，
整理，得：x2﹣40x+375＝0，
解得：x1＝15，x2＝25（不合题意，舍去）．
答：该经销商想要每天获得150元的销售利润，销售价应定为15元．
如图，已知平行四边形ABCD的两条对角线相交于点O，E是BO的中点，
过B点作AC的平行线，交CE的延长线于点F，连接BF．
（1）求证：FB＝AO；
（2）平行四边形ABCD满足什么条件时，四边形AFBO是矩形？说明理由．
（1）证明：∵E是BO的中点，
∴OE＝BE，
∵BF∥AC，
∴∠BFE＝∠OCE，
在△BEF和△OEC中，
∠BFE=∠OCE∠BEF=∠OECBE=OE，
∴△BEF≌△OEC（AAS），
∴BF＝OC，
∵四边形ABCD是平行四边形，
∴OA＝OC，
∴FB＝AO；
（2）解：平行四边形ABCD是菱形时，四边形AFBO是矩形．理由如下：
由（1）可知，FB＝AO，
∵FB∥AC，
∴四边形AFBO是平行四边形，
∵平行四边形ABCD是菱形，
∴AC⊥BD，
∴∠AOB＝90°，
∴平行四边形AFBO是矩形．
23.已知反比例函数，点都在该反比例函数图象上．

(1)求反比例函数的表达式；
(2)当时，直接写出y的取值范围；
(3)若经过的直线与y轴交于点C，求的面积．
【答案】(1)
(2)
(3)2
【分析】（1）由点都在该反比例函数图象上，可得，
计算求解的值，进而可得反比例函数的表达式；
（2）由，可得当时，y随x的增大而减小，当时，，
进而可得时，y的取值范围；
（3）由（1）可得，，待定系数法求直线的解析式为，求得，根据，计算求解即可．
【详解】（1）解：∵点都在该反比例函数图象上，
∴，
解得，，
∴反比例函数的表达式为；
（2）解：∵，
∴当时，y随x的增大而减小，
当时，，
∴当时，y的取值范围是；
（3）解：由（1）可得，，
设直线的解析式为，
将，代入得，，
解得，
∴，
当，，则，
∴．
24 .如图1，在矩形ABCD中，k，E为CD边的中点，连接AE，延长AE交BC的延长线于F点，
在BC边上取一点G，连接AG，使AF为∠DAG的角平分线．

(1)求证：GE⊥AF；
(2)如图2，若k＝1，求的值；
(3)若点G将BC边分成1：2的两部分，直接写出k的值．
【答案】(1)见解析；
(2)；
(3)或
【分析】（1）想证明两条直线垂直，可想到两条直线的夹角为90°，及转化求角度问题，而利用等腰三角形底边中点的性质，中线垂直于底边，这样就转化为证明相关三角形为等腰三角形的问题，问题即可得到解决．
（2）利用k＝1，把相关线段所表示的式子找出来，集中到一个相关三角形中，利用直角三角形的性质，列出相关等式，解出方程的解，问题即可得到解决．
（3）若点G将BC边分成1：2的两部分，这时分2种情况，BG＝2GC或者BGGC，利用上边的分析，在同一直角三角形中，列出相关等式，解出方程的解，问题即可得到解决．
【详解】（1）证明：∵E为CD边的中点，
∴DE＝EC，
∵∠AED＝∠CEF，∠ADE＝∠ECF＝90°，
∴△ADE≌△CEF，
∴AE＝EF，即E为AF中点，
∵AF为∠DAG的角平分线，
∴∠GAE＝∠DAE，
又∵AD∥CF，
∴∠DAE＝∠GFE，
∴∠GAE＝∠GFE，
∴△AGE为等腰三角形，
∴GE⊥AF．
（2）设EC＝1个单位，GC＝x，
利用Rt△ABG列出方程：（2﹣x）2+4＝（2+x）2，
解得CG，BG，
∴
（3）①当BG＝2GC时，设GC＝x，则BG＝2x，
∵k，
∴AB ，
∵AG＝GF＝4x，
利用Rt△ABG列出方程：（4x）²＝（ ）²+（2x）²，
解得k．
②当BG＝2GC时，设GC＝2x，则BG＝x，
∵k，
∴AB ，
∵AG＝GF＝5x，
利用Rt△ABG列出方程：（5x）²＝（ ）²+（x）²，
解得k．
综上：或．
演讲内容
语言表达
仪表仪容
所占比例
30%
60%
10%
小丽得分
90
85
75