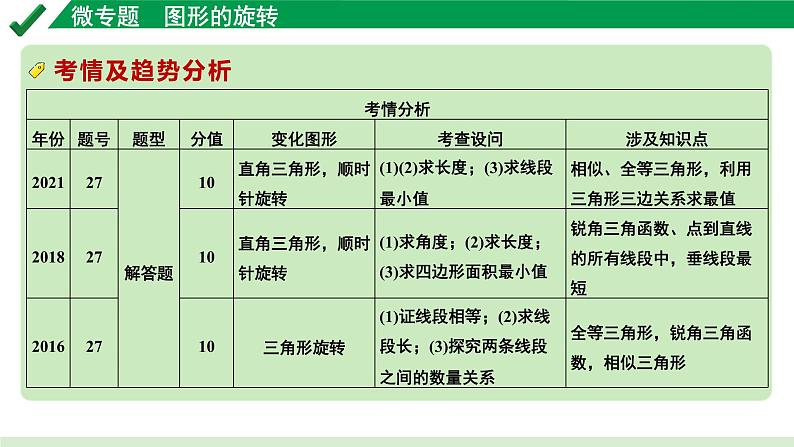
2024成都中考数学第一轮专题复习之第七章 微专题 图形的旋转 教学课件

这是一份2024成都中考数学第一轮专题复习之第七章 微专题 图形的旋转 教学课件，共21页。PPT课件主要包含了课标要求，考情及趋势分析，旋转角度，例题图①，例题图②，例题图③，例题图④，第1题图①，第1题图②，第1题解图②等内容，欢迎下载使用。

通过具体实例认识平面图形关于旋转中心的旋转．探索它的基本性质：一个图形和它经过旋转所得到的图形中，对应点到旋转中心距离相等，两组对应点分别与旋转中心连线所成的角相等．
图形旋转的要素及性质：1. 要素：旋转中心、旋转方向和____________．2. 性质：(1)对应点到旋转中心的距离____________；(2)对应点与旋转中心连线所成的角都____________旋转角；(3)旋转前、后的图形____________．
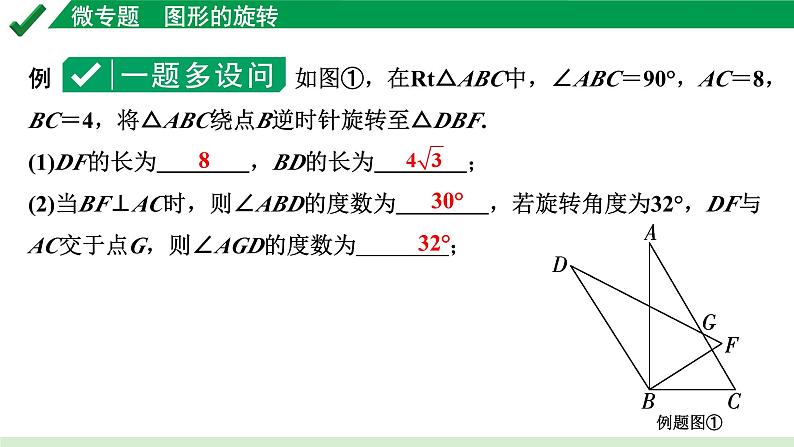
例　 如图①，在Rt△ABC中，∠ABC＝90°，AC＝8，BC＝4，将△ABC绕点B逆时针旋转至△DBF.(1)DF的长为　　　　，BD的长为　　　　；(2)当BF⊥AC时，则∠ABD的度数为　　　　，若旋转角度为32°，DF与AC交于点G，则∠AGD的度数为　　　　；
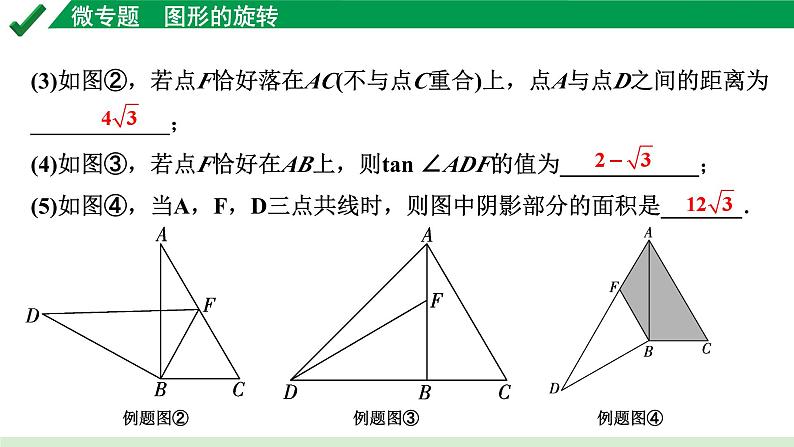
(3)如图②，若点F恰好落在AC(不与点C重合)上，点A与点D之间的距离为____________；(4)如图③，若点F恰好在AB上，则tan ∠ADF的值为____________；(5)如图④，当A，F，D三点共线时，则图中阴影部分的面积是_______．
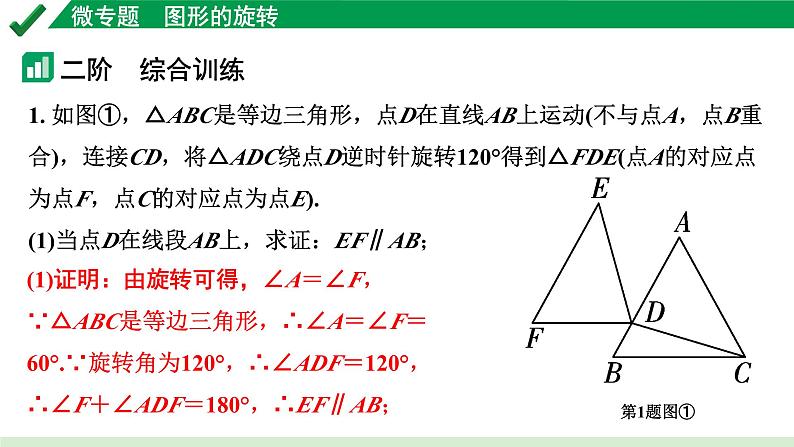
1. 如图①，△ABC是等边三角形，点D在直线AB上运动(不与点A，点B重合)，连接CD，将△ADC绕点D逆时针旋转120°得到△FDE(点A的对应点为点F，点C的对应点为点E).(1)当点D在线段AB上，求证：EF∥AB；
(1)证明：由旋转可得，∠A＝∠F，∵△ABC是等边三角形，∴∠A＝∠F＝60°.∵旋转角为120°，∴∠ADF＝120°，∴∠F＋∠ADF＝180°，∴EF∥AB；
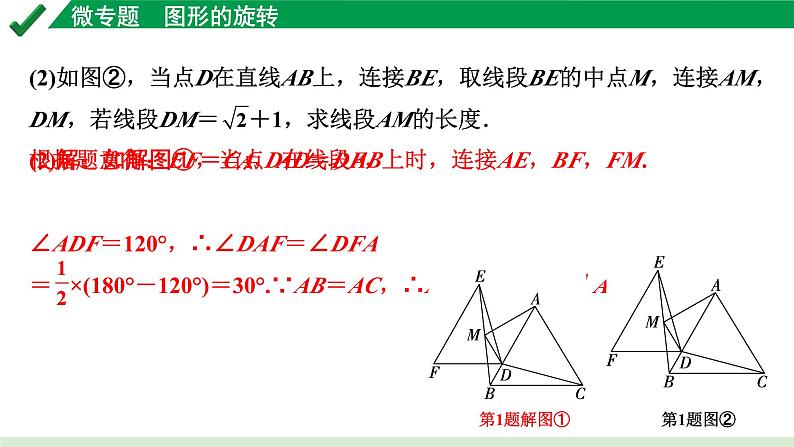
(2)如图②，当点D在直线AB上，连接BE，取线段BE的中点M，连接AM，DM，若线段DM＝ ＋1，求线段AM的长度．
(2)解：如解图①，当点D在线段AB上时，连接AE，BF，FM.
∴四边形ABFE是平行四边形．∵点M是BE的中点，∴AM＝FM，∴DM⊥AF，∴tan ∠DAM＝tan 30°＝ .∵DM＝ ＋1，∴AM＝ ＋ .
如解图②，当点D在线段BA的延长线上时，连接AE，BF，FM，同理可得四边形ABFE是平行四边形，∴AM＝FM，∴DM⊥AF，∴tan ∠DAM＝tan 30°＝ .∵DM＝ ＋1，∴AM＝ ＋ .综上可得，AM＝ ＋ .
2. 在等腰△ADC和等腰△BEC中，∠ADC＝∠BEC＝90°，BC＜CD，将△BEC绕点C逆时针旋转，连接AB，点O为线段AB的中点，连接DO，EO.(1)如图①，当点B旋转到CD边上时，猜想线段DO与EO的位置关系和数量关系，并说明理由；
解：(1)DO⊥EO，DO＝EO；理由：当点B旋转到CD边上时，点E必在边AC上，∴∠AEB＝∠CEB＝90°，在Rt△ABE中，O是AB的中点，
∴OE＝OA＝ AB，∴∠BOE＝2∠BAE.在Rt△ABD中，O是AB的中点，∴OD＝OA＝ AB，∴OD＝OE，∠DOB＝2∠BAD，∵△ADC是等腰三角形，且∠ADC＝90°，∴∠DAC＝45°，∴∠DOE＝∠BOE＋∠DOB＝2∠BAE＋2∠BAD＝2(∠BAE＋∠DAE)＝2∠DAC＝90°，∴OD⊥OE；
(2)如图②，当点B旋转到AC边上时，(1)中的结论是否成立？若成立，请写出证明过程，若不成立，请说明理由；
∵O是AB的中点，∴OA＝OB，∵∠AOM＝∠BOE，∴△AOM≌△BOE(SAS)，
证明：如图，延长EO到点M，使得OM＝OE，连接AM，DM，DE，
∴∠MAO＝∠EBO，MA＝EB，∵△ACD和△CBE是等腰三角形，∠ADC＝∠CEB＝90°，∴∠CAD＝∠ACD＝∠EBC＝∠BCE＝45°，∵∠OBE＝180°－∠EBC＝135°，∴∠MAO＝135°，∴∠MAD＝∠MAO－∠DAC＝90°，∵∠DCE＝∠DCA＋∠BCE＝90°，∴∠MAD＝∠DCE，
∵MA＝EB，EB＝EC，∴MA＝EC，∵AD＝DC，∴△MAD≌△ECD(SAS)，∴MD＝ED，∠ADM＝∠CDE，∵∠CDE＋∠ADE＝90°，∴∠ADM＋∠ADE＝90°，∴∠MDE＝90°，∵MO＝EO，MD＝DE，∴OD是ME的垂直平分线，∴OD＝OE，OD⊥OE；
(3)若BC＝4，CD＝2 ，在△BEC绕点C逆时针旋转的过程中，当∠ACB＝60°时，求线段OD的长．
∵∠ADC＝∠BEC＝90°，∴∠DCE＝540°－90°－90°－∠OBE－∠BAD＝360°－∠OBE－∠BAD＝360°－∠OAM－∠BAD，∵∠DAM＋∠OAM＋∠BAD＝360°，∴∠DAM＝360°－∠OAM－∠BAD，∴∠DAM＝∠DCE，∵AD＝CD，∴△DAM≌△DCE(SAS)，∴DM＝DE，∠ADM＝∠CDE，
∴∠EDM＝∠ADM＋∠ADE＝∠CDE＋∠ADE＝∠ADC＝90°，∴△MDE是等腰直角三角形，∵OM＝OE，∴OD＝OE＝ ME，∠DOE＝90°，在Rt△BCE中，∠BEC＝90°，BE＝CE，∴CE＝ BC＝2 ，过点E作EH⊥DC交DC的延长线于点H，在Rt△CHE中，∠CHE＝90°，∠ECH＝180°－∠ACD－∠ACB－∠BCE＝180°－45°－60°－45°＝30°，
∴EH＝ CE＝ ，∴CH＝ ＝ EH＝ ，∴DH＝CD＋CH＝3 ，在Rt△DHE中，根据勾股定理得，DE＝ ＝2 ，∴OD＝ DE＝2 ，
②当点B在AC右侧时，如解图，同①的方法得，OD＝OE，∠DOE＝90°，连接DE，过点E作EH⊥CD于点H，在Rt△EHC中，∠ECH＝30°，∴EH＝ CE＝ ，∴CH＝ ＝ ，∴DH＝CD－CH＝ ，在Rt△DHE中，根据勾股定理得，DE＝ ＝2 ，∴OD＝ DE＝2，综上可知：线段OD的长为2或2 .
分点B在AC左侧，点B在AC右侧两种情况讨论．